This site is being phased out.
Properties of homology groups
Redirect to:
In this article we establish connections between the topology of cell complexes and their homology.
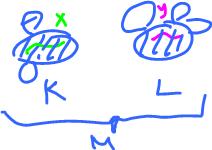
Theorem. For any finite cell complex $K$, it is path-connected iff $$H_0(K) = {\bf R}.$$
Proof. We already know (
) that $K$ is path-connected iff every two vertices can be connected by a sequence of edges, i.e., they are homologous. Suppose $A_1, A_2, \ldots , A_s$ are the vertices of $K$. Then, the above property has a clear algebraic meaning:
Let's look at the algebra: $$\begin{array}{l} C_0(K) &= {\rm span}\{A_1, A_2, \ldots, A_s \}, \\ Z_0(K) &= C_k(K) = {\rm span}\{ A_1, A_2, \ldots, A_s \}, \\ B_0(K) &= {\rm im \hspace{3pt}} \partial \colon C_1(K) \rightarrow C_0(K) \\ &= {\rm span} \{A_i - A_j \colon i,j = 1,2,...,s \}, {\rm \hspace{3pt} from \hspace{3pt} the \hspace{3pt} above \hspace{3pt} property} \\ &= {\rm span}\{A_2 - A_1, A_3 - A_1, \ldots , A_s - A_1 \}, \end{array}$$
since only these are linearly independent. Then $$\begin{array}{l} {\rm dim \hspace{3pt}}Z_0(K) = s, \\ {\rm dim \hspace{3pt}}B_0(K) = s - 1, \\ {\rm dim \hspace{3pt}}H_0(K) = 1. \end{array}$$
Hence $$H_0(K) = {\bf R} = {\rm span}\{A_i \}$$
for any $i$. Prove the converse as an exercise. $\blacksquare$
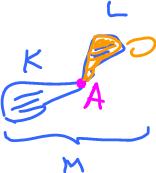
Theorem. For any finite cell complexes $K$ and $L$ with disjoint realizations, the homology group of the union is the product of their homology groups: $$H_k(K \cup L) = H_k(K) \times H_k(L).$$
Proof. Let $M = K \cup L$. Observe that $K$ and $L$ have no cells in common. So, none of the elements of the basis of the chain group $C_k(K)$ (cells in $K$) can be expressed as a linear combination of elements of $C_k(L)$ (cells in $L$), or vice versa. Therefore, we can re-interpret addition in $C_k(M)$: $$x + y = (x, y), {\rm \hspace{3pt} for \hspace{3pt}} x \in C_k(K), y \in C_k(L).$$
In other words, $$C_k(M) = C_k(K) \times C_k(L).$$
Next, $K$ and $L$ have no boundaries in common. Therefore,
$∂_M(x + y) = ∂_K(x) + ∂_L(y)$, or
Then, the computation of the boundary groups and the cycle groups of $M$ breaks into computation of those for $K$ and $L$:
$Z_k(M)$ = ${\rm ker}$ $\partial_M = {\rm ker \hspace{3pt}} \partial_K \times {\rm \hspace{3pt} ker \hspace{3pt}} \partial_L = Z_k(K) \times Z_k(L).$
Finally, $$\begin{array}{l} H_k(M) &= Z_k(M)) / B_k(M)) \\ &= [ Z_k(K) \times Z_k(L) ] / [ B_k(K) \times B_k(L) ] \\ &= [ Z_k(K) / B_k(K) ] \times [ Z_k(L) / B_k(L) ] \\ &= H_k(K) \times H_k(L), \end{array}$$
using facts from linear algebra. $\blacksquare$
Exercise. What if $M$ is the one-point union of $K$ and $L$? Provide analysis similar to the one above. Hint: start with Betti numbers.
Exercise. What happens to the homology groups of a cell complex if you add a new edge?
By creating new complexes from old we can sometimes express the homology of the new complex in terms of the old one(s):
Fact from linear algebra: all vector spaces of the same (finite) dimension are isomorphic. Therefore, for homology as a vector space, Betti numbers determine the homology, up to isomorphism. However, finding the homology means finding a basis explicitly.
The most important property of homology is that it is a topological invariant.
See also Homology of surfaces.
