Hodge duality of cubical forms

Redirect to:

• Geometry

Discrete forms in dimension 1

Discrete forms are supposed to mimic the behavior of continuous differential forms. That will take extra work.

Let's consider the trivial case of dimension $1$.

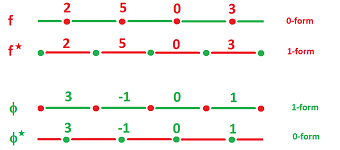
• If $f$ is a $0$-form then $f^*$ is a $1$-form with the same values.
• If $\phi$ is a $1$-form then $\phi ^*$ is a $0$-form with the same values.

However, in the discrete case $k$-forms are defined on $k$-cells. Therefore, these new forms will have to be defined on a new set of cells! For example,

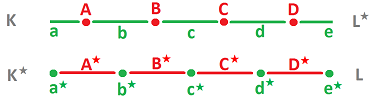
• If $f(A)=2$ for some $0$-cell $A$, there should be somewhere a $1$-cell, say, $A^*$ so we can have $f^*(A^*)=2$.
• If $\phi(a)=3$ for some $1$-cell $a$, there should be somewhere a $0$-cell, say, $a^*$ so we can have $\phi^*(a^*)=3$.

We call $A^*$ the dual cell of $A$ and $a^*$ the dual cell of $a^*$.

As you can see we assemble these new cells into a new grid, the dual grid:

We define a correspondence between original, called primary, cells and the dual cells. $$\begin{align*} 1{\rm -cell \hspace{3pt} (primary)} &\longleftrightarrow 0{\rm -cell \hspace{3pt} (dual)} \\ 0{\rm -cell \hspace{3pt} (primary)} &\longleftrightarrow 1{\rm -cell \hspace{3pt} (dual)} \end{align*}$$

For convenience we assume that these cells are related to each other geometrically, as follows:

• If $a$ is a $1$-cell then $a^*$ is a $0$-cell located at the center of $a$.
• If $A$ is a $0$-cell then $A^*$ is a $1$-cell centered at $A$.

The result is a "staggered" grid of cells.

To combine the two,

each $k$-cell in the primary grid corresponds to a $(1-k)$-cell in the dual grid.

This is what is happening in dimension $1$, illustrated with Excel:

Link to the file: Hodge_duality_dim_1.xlsx

If we have a cubical complex $K$ then the set of all of the duals of the cells of $K$ is the dual complex $K^*$.

Unfortunately, $K^*$ doesn't have to be a cubical complex as some of the boundary cell might be missing. For example, the dual of a single vertex complex $K=\{A\}$ is a single edge "complex" $K^*=\{A^*\}$. The end point of this edge aren't included. This result it typical in the sense that the dual of a "closed" complex is an "open" complex. The solution is either to include in $K^*$ all boundary cells of all the dual cells of $K$ or exclude all dual cells that have missing boundary cells.

With this definition, we can see now the duality of forms as well. Algebraically, if $f$ is a $0$-form over the primary complex, then define $$f^*(a)=f(a^*).$$ for any $1$-cell $a$ in the dual complex. And in the case of a $1$-form over the dual complex: $$\phi^*(A)=\phi(A^*)$$ for any $0$-cell $A$ in the dual complex.

To put this together we write: $$\psi^*(\sigma)=\psi(\sigma ^*),$$ where

• $\psi$ is a $0$-form and $\sigma$ is a $1$-cell, or
• $\psi$ is a $1$-form and $\sigma$ is a $0$-cell.

Of course, the star operator is now extended to chains by linearity.

With this arrangement we also ensure that we have $\star \star =Id$.

This works for $0$- and $1$-forms in dimension $1$, but the formula is used as a definition for all dimensions. Now we consider dual cells and dual complexes in dimensions $2$ and $3$.

Dual cells

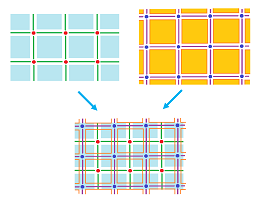
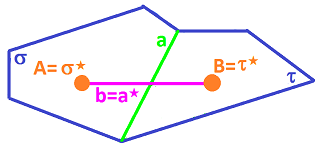
Given a "primary" cell complex $K$, its Hodge-dual complex $K^*$ is defined cell by cell, as follows, illustrated for cubical complexes in dimension $n=2$.

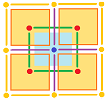
First, the dual of a cell in $K$ has the same center.

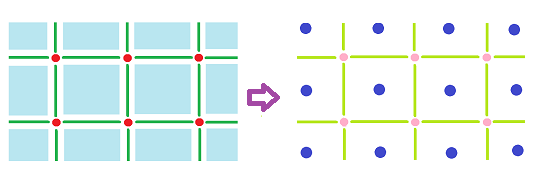
In fact, for the $2$-cells, their duals are $0$-cells, their centers:

What we see here is the squares shrinking to the dots.

Meanwhile, the $0$-cells are blown into the squares, if you go from right to left.

Next, the duality makes a $1$-cell turn around its center.

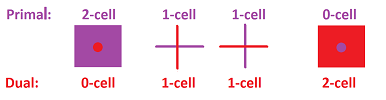
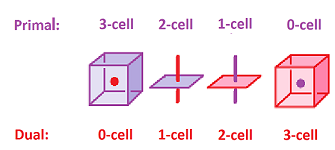
Generally, each (primary) $k$-cell $\alpha$ corresponds to a (dual) $(2-k)$-cell $\alpha^*$ with $\alpha^*$ centered at the center of $\alpha$.

The new grid is "staggered" again.

That's how you could build the dual of the whole-plane complex -- with the one-to-one correspondence. And, in fact, you can rebuild the primary complex from the dual following the same procedure.

Therefore for the whole plane, it's simple, We have below a primary grid along with the dual grid, with the two overlapping each other in the third illustration:

What happens if we have non-trivial cubical complex $K$ in ${\bf R}^2$? Just as in dimension $1$, some cells are missing as the example shows:

So, in general, $$K^{**} \neq K.$$

To see Hodge duality in Excel, simply re-size the rows and columns making the narrow ones wide and the wide ones narrow:

There is more going on in ${\bf R}^3$:

As before, the $k$-cells and the $(n-k)$-cells are paired up. If this looks like the orthogonal complement, it's because it is, see Hodge duality. We just observe that the dual of a cube $Q$ is the cube of the orthogonal complement of the span of $Q$.

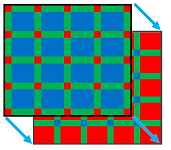
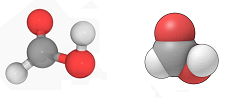
To illustrate the idea of duality in dimension $3$ one may consider the two ways a chemist would depict molecules:

The two equally valid ways are either

• small balls connected by rods, or
• large balloons pressed against each other.

For completeness sake, this is what Hodge duality looks like in the case of a general $2$-dimensional cell complex:

The dual is still located at the center of mass...

Hodge duality as a linear operator on chains

Above we only indicated what is the correspondence between cell is, geometrically. Now, we also have to keep track of their orientations.

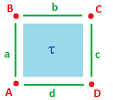
In particular, in dimension $2$ combining two $1$-cells may produce different orientations and, therefore, different signs:

Here $a \times d=\tau$ but $d \times a =-\tau$. So, the duality operator will produce different signs: $$([0,1]\times \{0\})^*=\{0\}\times [0,1],$$ $$(\{0\}\times [0,1])^* = -[0,1]\times \{0\}.$$

Therefore, we need to treat Hodge duality as an operator on chains: $$\star :C_k(K)\rightarrow C_{n-k}(K^*).$$

An obvious observation is that, since for any cell we have $$\alpha^{**}=(-1)^?\alpha,$$ then $$\star\star=(-1)^?Id.$$

For the value of this sign depends on the dimension $n$ of the space and the degree $k$ of the cell: $(-1)^{k(n-k)}$. For details, see Hodge duality.