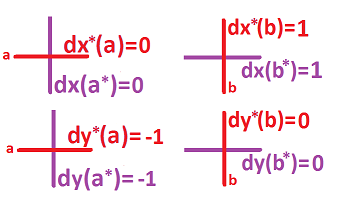Dual cells and dual forms

Redirect to:

Duality in ${\bf R}^2$

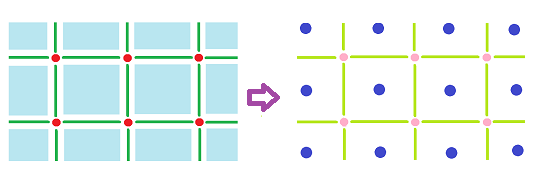
What is the dual of a cell on the plane?

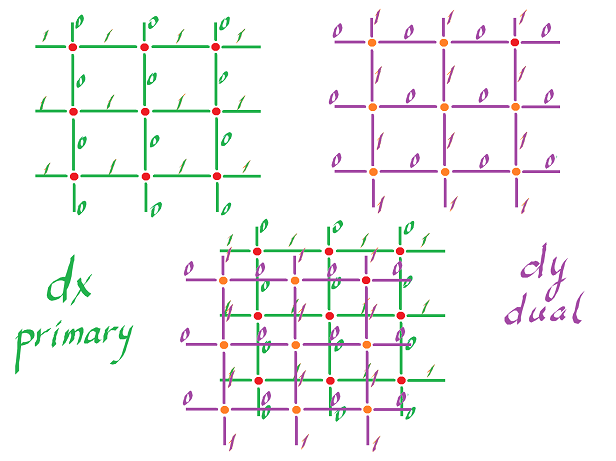
We define the dual grid "outside the box" with the same idea: the dual of a cell has the same center.

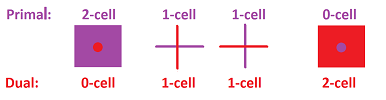
For a $2$-cell, the dual is its center:

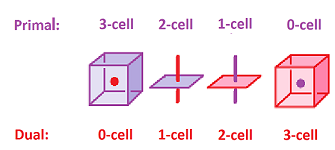
Each $k$-cell (primary) $\alpha$ corresponds to a $(2-k)$-cell (dual) $\alpha^*$ with $\alpha^*$ centered at the center of $\alpha$.

Important observation:

Theorem. For any cell, $$\alpha^{**}=\alpha$$

Therefore for the whole plane, it's simple:

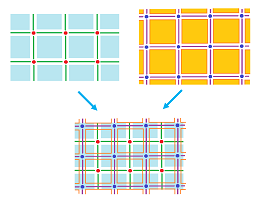
What happens if we have non-trivial cubical complex $R \subset {\bf R}^2$? Some extra work is required as the example shows:

So, in general, $$R^{**} \neq R.$$

Example: Let's verify $(dx)^* = dy$, $(dy)^*=dx$.

For either one, just turn $90^o$ and assign the same number (in the case of Euclidean geometry).

To be exact, this is how we find the values on $1$-cell for $(dx)^*$:

We find $(dx)^*$ from definition above, $(dx)^*(a) = dx(a^*)$, where $a$ is a dual cell and $a^*$ is a primary cell:

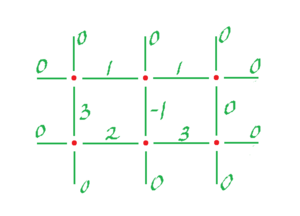
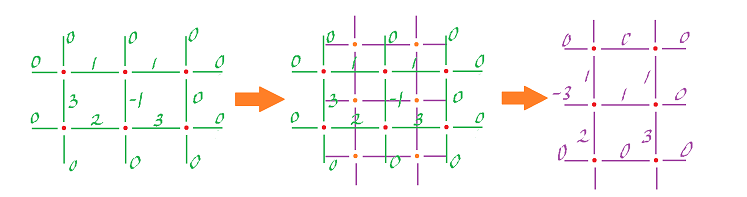
Example: This is a $1$-form $\varphi$:

Find the $1$-form $\varphi^*$:

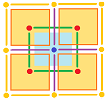
There is more going on in ${\bf R}^3$:

Note: This looks very much like the orthogonal complement in linear algebra.