When is a cubical complex a surface?

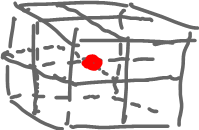
We consider surfaces in the 3D grid.

Our approach:

• a) Given $A$, a point in ${\bf R}^3$ grid. Illustrate all possible arrangements of faces adjacent to $A$ so that their union is homeomorphic to a disk.
• b) Come up with necessary and sufficient condition for a $2$-complex on the grid to be a $2$-manifold, in terms of arrangements of faces adjacent to $A$.

For a), there are four cases:

There are three other ways to label the second picture, but we let that one count for all of them because they can be moved to each other by rotations.

How can we prove that's it?

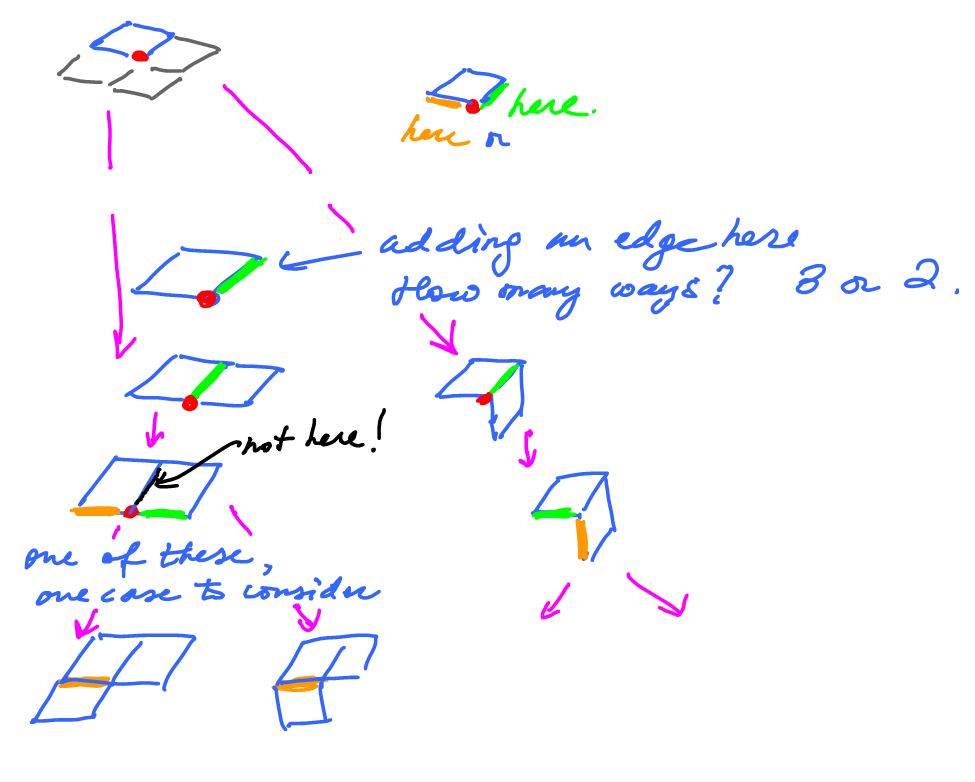
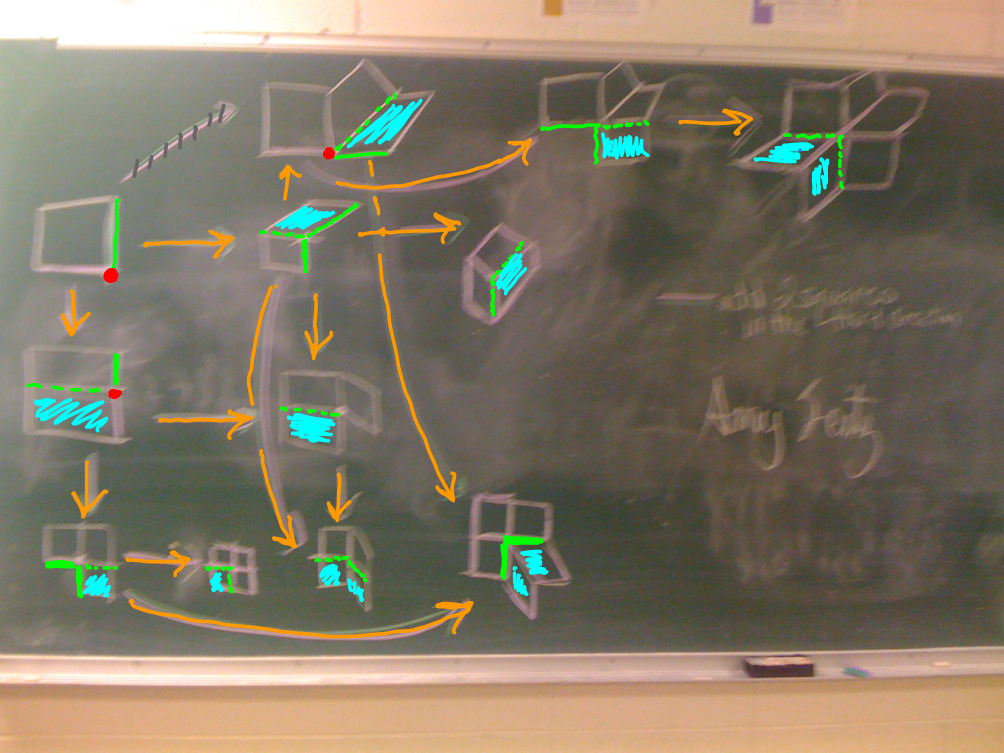
Stage 1: Start with $A$ in the middle of the $2 \times 2$ box and start adding faces, adjacent to $A$.

How many: 12 (Stage 1). Cases to consider: 1.

Stage 2: Add another face (square).

Cases to consider: 1.

Proceed...

Finish (exercise).

For b).

The faces containing $A$ can be arranged in a circle: they are $F_0, F_1, \ldots, F_s = F_0$ and if $|i-j|=1 {\rm mod} s$ then $F_i$ and $F_j$ share one edge. Otherwise, $F_i$ and $F_j$ don't share edges.