This site is being phased out.
What shape of sword is best for cutting?
The book contains lists of problems for final projects. Their statements are very brief but the two main expectations are:
- the projects are meant to be practical and exploratory, and
- their solutions are supposed to rely exclusively on the material presented in the book.
To make clearer what's expected, I present a sample of such a solution. The topic is meant for Part III: "What is the perfect shape of a sword for cutting?" The nice thing about this project is this (spoiler!): there is a mathematically satisfying answer. Such an outcome is not however something that we expect from a typical project.
To begin with, why is a curved blade better for cutting than a straight blade?
Of course one can cut with a straight blade and cut well. These are a kitchen knife and the guillotine:
These are the arming sword and the rapier:
You can cut with any sharp piece of metal. But is there any disadvantage in using a straight edge?
What makes a difference is how the blade penetrates the medium. Below, we assume that the blade is already in the medium rather then just starting to penetrate.
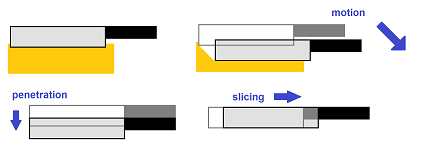
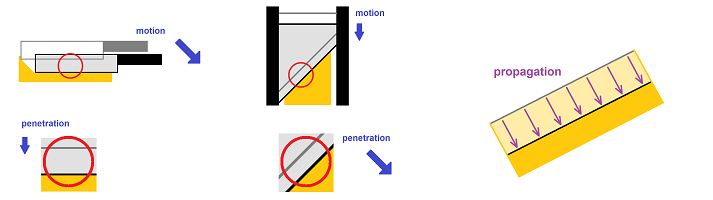
Let's take a look at what a kitchen knife does to a piece of cheese.
Even though the knife is pulled back, the edge is moving vertically. We come to this realization when we focus on a small part of the surface of the medium. We also see that the “front” of the cut propagates uniformly: all of its points are moving at the same speed. In addition, all points are moving in the same direction.
Now the guillotine. The dynamics is the same except its knife has a slope and the edge seems to be moving vertically:
However, the actual penetration is still perpendicular to the edge of the blade. The “front” of the cut still propagates uniformly (through the cheese).
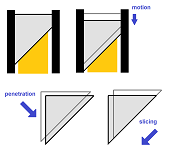
If we zoom in on either of the two blades, there is no difference in how they operate:
We have decomposed the motion into two parts:
- the penetration, which is perpendicular to the edge, and
- the slicing, aka “sawing”, which is parallel to the edge.
(Note that the idea of decomposition of vectors is routinely used in physics, e.g., in the study of motion of an object on a sloped plane.)
We won't try to evaluate the amount of sawing here and only concentrate on penetration. In fact, we will follow this simple idea: $$\text{penetration of the blade }\ =\ \text{ propagation of the cut.}$$
So far, the most important observation about how these two blades work is that the motion is linear. That is why the penetration, and the propagation of the cut, is uniform.
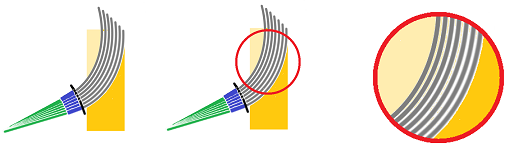
Now the swords. This isn't how swords move and this isn't not how they penetrate: the difference, and the issue we have to address, is the rotation of the sword.
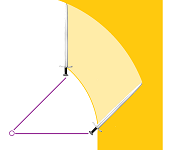
At its simplest, cutting is a chopping motion: the shoulder serves as the axis of rotation while the wrist and the elbow are locked. As a result, the sword is being rotated. That is why the tip of the blade is moving faster than its base:
Here, and below, we assume that:
- the arm is about the same length as the sword,
- the sword is held at $45$ degrees or $0$ degrees to the arm,
- the arm is swung through $45$ degrees.
We take the fact that the tip of the blade is moving faster than its base as the evidence that the propagation of the front of the cut is non-uniform. Why is this important? We know that the resistance of the medium is dependent on the speed of propagation; it may be proportional to the speed or even to its square. As a result, the blade will slow down non-uniformly and this will cause the tip of the sword to be pushed in the direction opposite to the swing. In turn, the sword will push back your wrist.
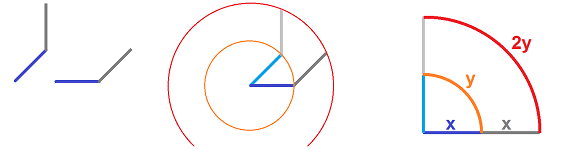
Specifically, let's consider the simplest case when the length of the blade is equal to the length of the arm and the wrist is locked at $0$ degree (shown on far right). Then, the tip of the sword travels twice the distance the hilt does and, therefore, the tip goes twice the speed of the hilt. If one to cut with, say, the middle third of the blade, the speed will vary by $25\%$.
Thus, the top is slowed down relatively by the extra medium to pass through but, because the sword is rigid, the rest is also slowed down. This complex motion-control problem is routinely solved by a skillful swordsman. However, our interest here is to imagine a weapon that requires the least amount of training (such as a machete) and still produces a good cut.
One can try to mitigate the problem by making the blade heavier toward the end. For example, these are the dao and the falchion:
However, the drawback isn't just the extra weight; the tip of the blade is less maneuverable which makes it hard to thrust and to parry. The extra width will also add extra friction and impede deep penetration. This is why below we will deal only with the edge itself.
So, why is it better to cut with a curved edge? The curving changes how fast different parts of the blade move. The result may be a more uniform penetration: ideally all parts of the cut propagate at the same speed. Note that, because of the rotation of the blade, we can't make all parts progress in the same direction in addition to the same speed unlike the two blades we started with.
Blades vary in curvature. These are the katana and the saber:
They have the least amount of curving. The next two have more; these are the talwar and the shamshir:
As you can see, the curvature varies within each sword. Note however that the flatness of the blade close to the hilt should be ignored as this part is not involved in cutting.
Below you can see the difference in the distance traveled by the tip (saber vs. shamshir and $45$ degrees vs. $90$ degrees):
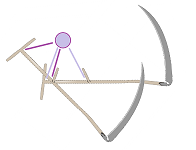
This is the scythe:
Even though this is not a sword and its edge is on the opposite side of the curve, it does cut and it cuts via a circular motion. Just as a sword, the scythe needs a sophisticated blade in order to make thousands of cuts... We can see how in this case the tip is actually moving slower than the base.
What is the best shape? The conjecture is that it is the one that has the front progressing at a constant speed during the strike, even though the directions of different parts (perpendicular to the front) may vary. This is what uniform propagation looks like:
This can't be a circle as its radius would have to be increasing. We can observe the non-uniformity of propagation for the shamshir:
Let's now try some mathematical curves. At the very least, the sword shouldn't come back when swung, hence the question in part becomes: “Is there a curve on the plane that when rotated around the origin doesn't intersect the original?”.
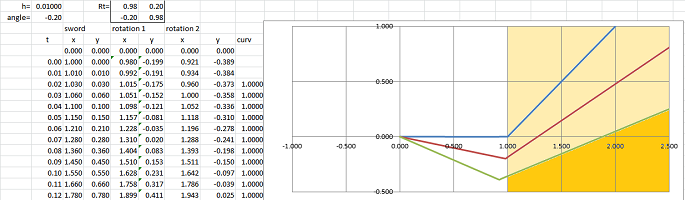
We start with the “arm” plotted as the segment from $(0,0)$ to $(1,0)$. The former point is the “shoulder” and the latter is the “wrist”. Starting from the latter, we plot a parametric curve, $$x=x(t),\ y=y(t),\ t\ge 0,$$ with a spreadsheet. We set up three columns -- for $t$, $x$, and $y$ -- and then insert a “smooth scatter-plot” for the last two (blue):
Next, this curve is rotated. It is done with the help of the rotation matrix (shown at the top) for an angle of rotation $\alpha$: $$R=\left[\begin{array}{rrr} \cos \alpha &-\sin \alpha\\ \sin \alpha &\cos \alpha\\ \end{array}\right].$$ The matrix is applied to every point on the curve and the result is a new parametric curve given in the next two columns. The new curve is then plotted (red). Next, it is then rotated one more time and plotted again (green).
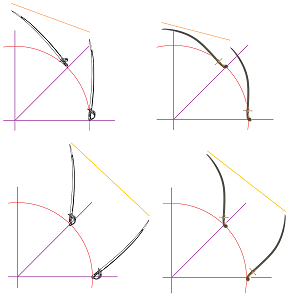
The first example is a straight line (curvature $0$): $$x=t+1,\ y=t,\ t\ge 0.$$ The result is shown above and it is the same as what we discussed previously.
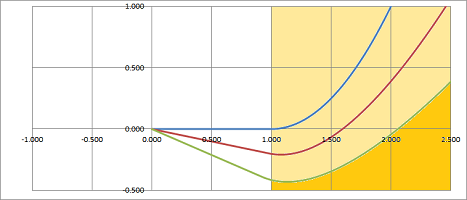
Next example is a parabola: $$x=t+1,\ y=(t-1)^2-1,\ t\ge 0.$$
We, again, observe a growing separation of the rotated curve from the original.
For either kind of curve, if we extend it backward, the new curve will intersect the original. This means that the distance between them is zero at that point. So, this distance must be growing and, therefore, cannot be constant. We, then, need a curve that, when rotated, doesn't intersect itself, at least.
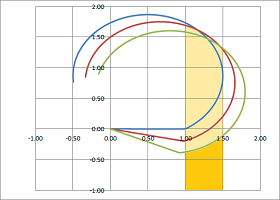
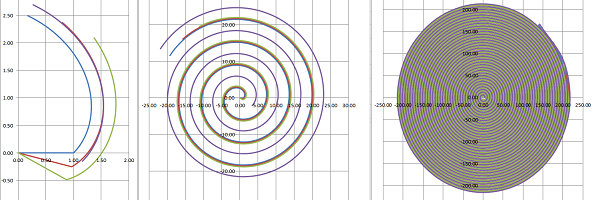
It seems that we need more curvature... Let's try a circle (curvature $1$): $$x=\frac{1}{2} \cos t,\ y=\frac{\sqrt{3}}{2}+\frac{1}{2} \sin t,\ t\ge 0.$$
We see intersections again. This time they appear when we extend the curves forward. Now we have too much curvature... What if the curvature is slowly decreasing? A spiral might be the answer. Let's try this, one of the simplest, spirals: $$x=(1+t)\cos t,\ y=(1+t)\sin t,\ t\ge 0.$$ It is “held” at $45$ degrees:
We can see on the right that the curve appears to behave well: the curve and its rotated version remain together but don't cross!
So, the rotated version looks like the propagated version of the curve. To confirm this conclusion, we take this construction one step further: we will show that the propagated version looks like the rotated version.
But first, this is how it is done in general. The front propagates in the direction perpendicular to itself. In the case of a curve, this direction is different at different locations: we take it to be the direction perpendicular to the tangent line at that point. This is what a uniform propagation -- the speed is the same at all locations -- looks like:
In the case of a curve made of pieces, such our scatter-plot, the construction is simple: we take every edge between two consecutive points, turn it $90$ degrees, and then proceed a unit of length in that direction.
This is the result of such a propagation of our spiral (purple):
Even though the curves appear to stay together long term, on a smaller scale the match is only approximate! This is not the perfect curve.
This concludes the heuristic part of the project.
As we want to go beyond approximations, we search for a curve with the property that we want: the rotated version of the curve has a constant separation distance from the original. Of course, we measure the separation along those perpendicular lines as discussed above.
There is in fact such a curve and it is used in the actual cheese slicers. It is called the involute of a circle: $$x=\cos t +t\sin t,\ y=\sin t-t\cos t.$$ This is a curve obtained by attaching a taut string to a circle and tracing its free end as it is wound onto the circle. To a naked eye, it looks exactly the same as the spiral we have been discussing.
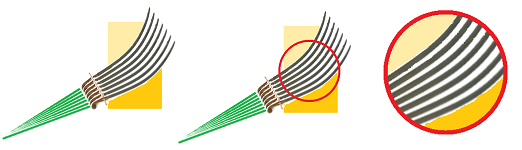
This is what the involute sword looks like:
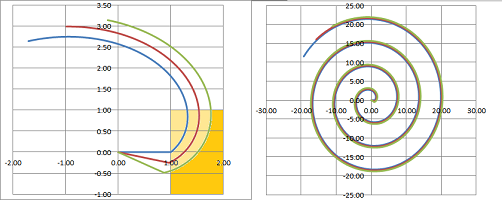
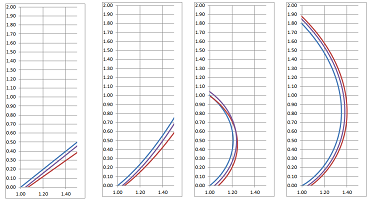
We notice that, in contrast with other swords above, the curvature is decreasing towards the tip. Below, we plot four curves that start at $(1,0)$ at $45$ degrees: a straight line, a parabola, a circle, and this spiral:
We see three curves: the blade (blue), its propagation (purple), and its rotation (red). Only the last one has them parallel to each other...
One can see how uniform the propagation is when this sword is swung:
Appendix. Just to confirm that we have a historically accurate approach, I include a few excerpts from a book published in 1860, Memoir on Swords, by Marey-Monge, Guillaume Stanislaus, translated from the French by Maxwell, Henry Hamilton.
P. 14-15. It is not necessary that the cutting edge should be inclined to the origin of the blade to produce the effect of a more acute edge; it is merely requisite to alter the direction of the force of the blow, by causing the edge to glide upon the object struck by a peculiar motion of the wrist from front to rear. This is practiced in the broadsword exercise, in which the combatant endeavours to keep his point opposite his adversary's body as far as possible; this is termed "sawing". A sensible effect of velocity thus obtained, without which penetration would have perhaps been impossible. The normal velocity in this cut, which is almost tangential, is feeble; consequently the steel has but a slight effect in compression the flesh, which merely sustains a feeble pressure in a normal direction.
P. 16. Thus, when the edge is perpendicular to the stroke, it penetrates like a wedge having the same angles; but when it is oblique to the direction of the motion, it penetrates as though the angle of the edge were more acute, and this effect increases with the obliquity. This advantage may be obtained by making the blow in the ordinary direction, and with the usual velocity, but having the edge oblique, or the edge being straight, by causing it to act with a sawing motion.
p. 19. The velocity of the point of the sword, in making a cut which produces a great effect with the edge, may be estimated perhaps at about fifty metres (164 feet) per seconds. In the cut, a sword should be considered in the light of a projectile, of which the portion in the neighborhood of the point has a much greater velocity than the hilt. The hand gives it this impulse, and does not act by pressing the sword on the body to be penetrated at the moment of impact.
At the moment of impact, the whole of the sword moves with an impulse perpendicular to the object struck, but with a velocity diminishing from point to hilt.
Further work:
- Evaluating the Ability of Different Blades by Jacob Hesson
- How do you cut with a straight blade? Design the “pull” for this and other blades.