This site is being phased out.
The political spectrum is a circle
Below we give an example of emergence of topological features in data and then discuss the possible consequences of this fact.
First, we will investigate the political spectrum as data.
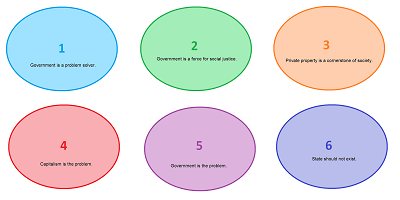
Suppose we have conducted a poll that consists of the following six statements (in random order) offered to every person to agree or disagree:
- 1. Government is a problem solver.
- 2. Government is a force for social justice.
- 3. Private property is a cornerstone of society.
- 4. Capitalism is the problem.
- 5. Government is the problem.
- 6. State should not exist.
According to the rules of the poll, there is no way to express the degree of agreement or disagreement as “Yes/No” (or “True/False”) are the only possible answers in the questionnaire. After the data has been collected, what, in addition to the relative popularity of each political creed, can we say about the spectrum of opinions that has emerged?
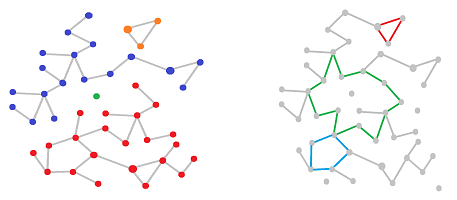
To a naked eye, the poll data consists only of the $6$ lists (longer or shorter) of people that support each of the $6$ statements:
Our visualization of the data is just these six lumps.
Now, is there any structure within this data? Is there a way to tell if two given statements are close to each other? No. However, we can say that two given statements are “related” to each other -- whenever there is at least one person who supports both. In other words, the two sets of supporters intersect. We then realize that the poll data contains much more information:
- the $6$ lists of people that support each of the $6$ statements,
- the $6(6-1)/2=15$ lists of people who support each pair of statements, etc.
We make the following simplifying assumptions about the support for the political creeds in this poll:
- (1) every person supports at least one of these statements, and
- (2) no person supports more than two.
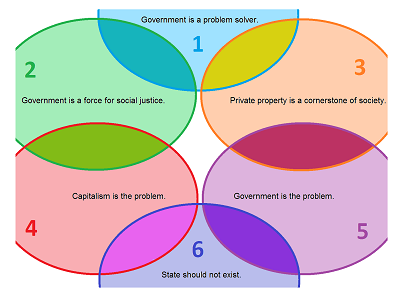
Then the poll data might look like this: $$\begin{array}{c|cccccc} & 1 &2 &3 &4 &5 &6\\ \hline 1 &\blacksquare&\times &\times & & & \\ 2 &\times &\blacksquare& &\times & & \\ 3 &\times & &\blacksquare& &\times & \\ 4 & &\times & &\blacksquare& &\times \\ 5 & & &\times & &\blacksquare&\times \\ 6 & & & &\times &\times &\blacksquare \end{array}$$ We mark a cell with $\times$ when there are people that support the two statements, the one in the row and the one in the column.
Based on this data, we start moving those ovals around in our visualization; if two creeds have supporters in common we have the two ovals overlap, otherwise we keep them away from each other:
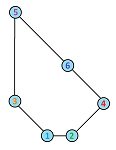
We have illustrated the statements and the relations between the statements. This is a map of our political landscape and it seems to have a hole!
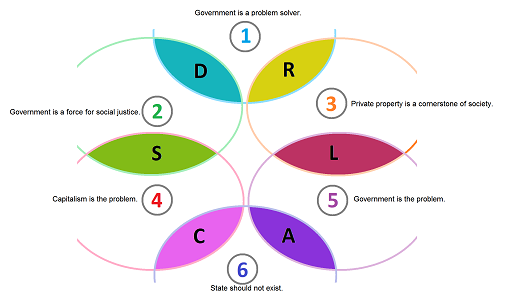
For convenience, we now assign (arbitrary) letters to the intersections of these sets:
- 1 and 2: $D$,
- 1 and 3: $R$,
- 2 and 4: $S$,
- 3 and 5: $L$,
- 4 and 6: $C$,
- 5 and 6: $A$.
We have classified all individuals based on which statements they support. In our visualization, in addition to numbers representing the statements, we now add letters to represent the relations between them:
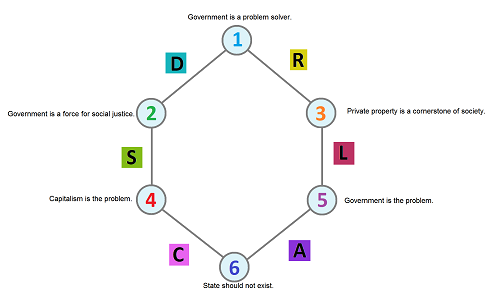
This point of view leads to a more compact visualization of the data, a graph:
- the nodes are the statements and
- the edges are the relations between them.
The resulting graph resembles a circle. Definitely a hole!
We should keep in mind that only one-on-one relations between the statements are captured in the data and, therefore, only the adjacency of the nodes is represented in the graph. That's why none of these following concepts apply: “left-right”, “close-far”, “extreme-moderate”, “between”, “opposite”, etc. Indeed, we can stretch the graph and even flip it and it will remain topologically the same:
We call such a graph a topological circle. In general, what is truly important is whether the graph representing the political spectrum has “topological features”; it may have breaks or it may have holes:
To summarize, the political spectrum is initially formed from nothing but political statements or creeds (nodes), then the relations between pairs of creeds (edges) are revealed from peoples' support. Our extremely simple model indicates the possibility that such topological features as breaks, holes (and even voids in more complex situations) are present in the political landscape.
When the data is more realistic, such a visual examination is no longer possible. The mechanism used to topologically evaluate data directly is called homology and it is the main subject of Topology Illustrated. Homology is also capable of handling the situations when there are more than just two supporters of each statements and graph representations become inadequate.
What makes the topological features important?
Let's consider our hypothetical political spectrum in the context of the so-called social choice theory. We think of our statements as votes.
Suppose the voters make selections from a list of choices. Suppose these choices are the nodes of some graph, which means that some of the choices are related just as in the example above. Now, what should be the collective decision? A choice function is a rule that to any possible combination of votes (an election) assigns a single outcome, the combined vote, and this outcome should be also one of the choices in the list and, therefore, a node of the graph.
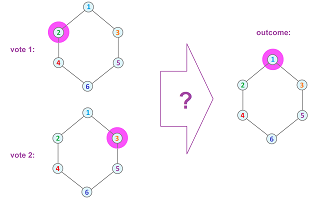
Below, we illustrate a hypothetical election with just two voters and six possible choices:
In order to ensure a fair compromise, the choice function is required to satisfy the following three conditions:
- Stability: if a single vote changes to a related one, the combined vote can also only change to a related one (or remain unchanged).
- Anonymity: if two votes are interchanged, the combined vote remains the same.
- Unanimity: if all votes are identical, the combined vote is that vote.
We can think of this function as -- non-algebraic but topological -- averaging. In the case of a physical object, we are talking about its center of mass:
Even though the requirements seem reasonable, such a procedure might be impossible! Indeed, if there are only two -- unrelated -- options, there can be no compromise. The conclusion is the same whenever the graph is disconnected. In fact, we know that the center of mass might lie outside the object. This means that the averaged vote might not be a vote itself:
It is a more subtle result that this insight applies to graphs.
Impossibility Theorem. Suppose the graph of choices contains a topological circle. Then there is no choice function that satisfies the three conditions above.
The theorem then suggests that, if those six political issues are put to a vote, there can be no electoral system that would always produce a fair compromise. This means that either one of the three requirements has to be abandoned or some of the political creeds have to be discarded beforehand.
The conclusion, though surprising, isn't entirely counter-intuitive. It is a common sense observation that excluding some options might make compromise impossible even when, as in our case, we can't point out what's missing. Of course, a compromise-producing rule also becomes impossible.
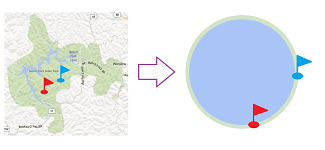
In the two examples below, it is clear what's missing. First, we can't develop a procedure for finding a fair compromise on a choice of location of a camp on the shore of a lake:
Second, a compromise on colors may also be impossible -- without gray:
For a rigorous presentation of the topic, see Topology Illustrated, the very last section.
Bonus question 1: what if we use the rules of the poll in the beginning of the article as the rules of the elections in the end?
Bonus question 2: what if the voters vote for the intersections?