This site is being phased out.
The expected value
The expected value
Suppose, once again, we have a system of weights $m_1,...,m_n$ located at $c_1,...,c_n$ points on the $x$-axis.
Suppose the weights are being distributed one at a time according to some unknown rule or possibly at random. What is the meaning the the center of mass of this system? It is our expectation of the next location.
The total moment with respect to $c$ $$\sum_i m_i (c_i-c)$$ is zero when $c$ is the expected value: $$c=\frac{\sum_i m_i c_i}{\sum_i m_i}.$$
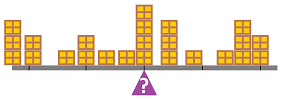
Example. A baker follows the price of wheat (USD per bushel) that changes every day. And now he wants to know what price to expect the following month, on average. He has been recording the price $y=p(x)$ at time $x$ but, being a busy man, he does this at random intervals. What to do? For each price he records its frequent, i.e., how many times is has occurred. He puts these numbers in a table, which makes a function. These may be its inputs and outputs: $$\begin{array}{l|cccc} y&0&1&2&...&10\\ \hline z=f(y)&1&3&2&...&0\\ \end{array}$$ This may look like a generic function but let's take a closer look at how the data is collected. It's not the exact value of either price that matters but rather its range, say $2\le x<3$. This range is an interval of values, say $[2,3]$. The data then is represented by a table that looks a bit different: $$\begin{array}{l|cccc} y&0&&1&&2&&3&...&9&&10\\ \hline &\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ z=f(y)&&1&&3&&2&&...&&0&\\ \end{array}$$ We are justified to visualize this information as bars over these intervals:
The average price combination is equivalent to finding the center of mass of the object made of bars.
When the bins are unequal, we have to deal with an arbitrary partition of the interval and, furthermore, the Riemann sums... $\square$