Projection map

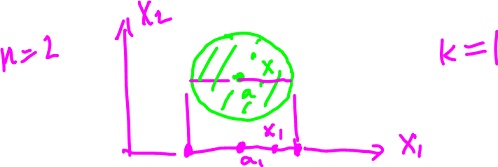
Let's limit our analysis to ${\bf R}^n$.

Theorem. Let $$f: {\bf R}^n {\rightarrow} {\bf R},$$ $$f^k(x) = x^k,$$ be the projection, where $$x = ( x_1, ..., x_n ).$$ Then $f$ is continuous.

(For example, if $n = 3, f_2 ( 1, 5, 7 ) = 5$.)

Proof. Consider

$f^k(x) = a^k$, where $a = ( a_1, ..., a_n )$.)

In order to show this, we have to find ${\delta}$ for a given ${\epsilon} > 0$. We hence want to show that for $$|| x - a || < {\delta} $$ it follows that $$| f^k(x) - f^k(a) | = | x^k - a^k | < {\epsilon}.$$

We rewrite $$( ( x_1 - a_1 )^2 + ( x_2 - a_2 )^2 + ... )^{\frac{1}{2}} < {\delta},$$ and $$( ( x_1 - a_1 )^2 + ( x_2 - a_2 )^2 + ... )^{\frac{1}{2}} ≥ ( ( x^k - a^k )^2 )^{\frac{1}{2}} = | x^k - a^k | < {\epsilon}.$$ Choose ${\delta} = {\epsilon}$. Then if $$( ( x_1 - a_1 )^2 + ( x_2 - a_2 )^2 + ... )^{\frac{1}{2}} < {\delta} = {\epsilon},$$ then

$| x^k - a^k | < {\epsilon}$. $\blacksquare$

The proof of continuity of the projection of the product topology is very similar.

Related: Radial projection.