Polar coordinates

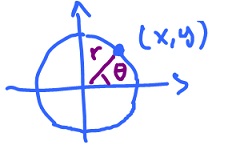
These are the transition formulas for Cartesian coordinates and back:

 ( x, y ) ↦ ( r, θ )  
 x = r cos θ ↔ r = ( x2 - y2 )1/2
 y = r sin θ ↔ θ = arctan y / x.

Integration

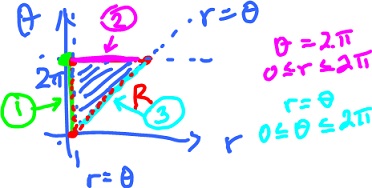
Find the area bounded by the curves:

 r = θ
 r = 0
 θ = 2π

Let's first plot these curves in in the ( r, θ )-plane.

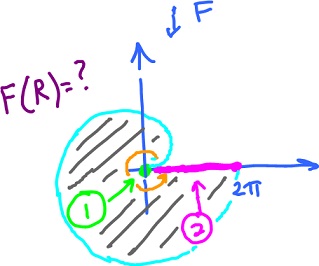
Now, the "polar coordinate map" F transforms R into a region in the (x,y)-plane.

 F: x = r cos(θ),
    y = r sin(θ);
 F: ℝ2 → ℝ2;
 F( r, θ ) = ( r cos(θ), r sin(θ) );

It is bounded by the curves:

 1) line r = 0:   F( 0, θ ) = ( 0, 0 );
 2) line θ = 2π:  F( r, 2π ) = ( r cos(2π), r sin(2π) ) = ( r, 0 ),   0 ≤ r ≤ 2π;
 3) line r = θ:   F( θ, θ ) = ( θ cos(θ), θ sin(θ) ),   0 ≤ θ ≤ 2π.

θ is the angle with respect to the x-axis. Then

 Area = ʃʃF(R) 1 dA = ʃʃR r dr dθ = ʃ02πʃr2π r dθ dr = …