This site is being phased out.
Midtearm
Precalculus -- Spring 2016 -- midterm
Name:_________________________ $\qquad$ 10 problems (out of 11), 10 points each
- Justify every step you make with as thorough an explanation as possible.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1. Find the domain of the function $\frac{1}{(x-1)(x^2+1)}$.
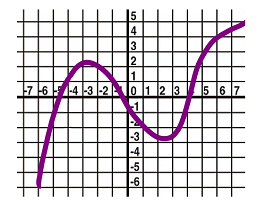
$\bullet$ 2. A sketch of the graph of a function $f$ is given below. Describe its behavior the function using words "decreasing" and "increasing".
$\bullet$ 3. Represent this function: $h(x)=\frac{x^3+1}{x^3-1},$ as the composition of two functions of variables $x$ and $y$.
$\bullet$ 4. Find the line passing through the point $(-1,2)$ and perpendicular to the line $y=-x-2016.$
$\bullet$ 5. Represent the composition of these two functions: $f(x)=\frac{1}{x}+1$ and $g(y)=\sqrt{y-1}$, as a single function $h$ of variable $x$. Don't simplify.
$\bullet$ 6. Solve the quadratic equation $x^{2}+2x+10=0$ and represent the answer in the standard form $a+bi$, where $a$ and $b$ are real numbers.
$\bullet$ 7. For the polynomial $f(x)=-2x^2(x+2)^2(x^2+1)$, find its $x$-intercepts.
$\bullet$ 8. Function $y=f(x)$ is given below by a list its values. Find its inverse as a similar table. $$\begin{array}{l|l|l|l}x &0 &1 &2 &3 &4 \\\hline y=f(x) &1 &2 &0 &4 &3 \end{array}$$
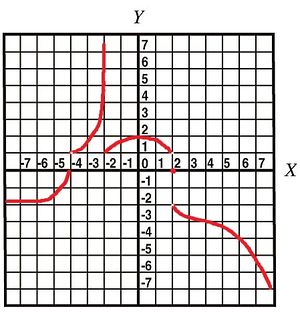
$\bullet$ 9. Plot the inverse of the function shown below, if possible.
$\bullet$ 10. Find a formula for a polynomial with these roots: $1$, $2$, and $3$.
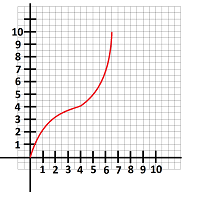
$\bullet$ 11. The function $y=f(x)$ shown below represents the location (in miles) of a hiker as a function of time (in hours). Find the hiker's average velocity.