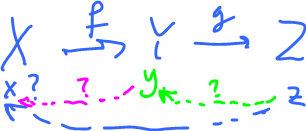Linear algebra: test 2

Grading

Test 2 for Linear algebra: course

6 problems, 10 points each

Instructions: Show enough work to justify your answers. Refer to theorems in the book whenever necessary.

1. Suppose $A$ is an invertible matrix. What is $(A^{m})^{-1}?$
2. Given basis $\{1,x,x^{2}\}$ of the space $\mathbf{P}_{2}$ of degree $\leq $2 polynomials, find the change of basis matrix for the new basis $\{2,x-x^{2},x-1\}.$
3. Suppose $V$ is the space of differentiable at $0$ functions of two variables. Suppose $A:V\longrightarrow \mathbf{R}^{2}$ is given by $A(f)=grad $ $f(0).$ Prove that $A$ is linear and find its kernel.
4. Prove that the composition of two onto functions is onto.
5. Given a (possibly infinite dimensional) vector space $V$ with basis $S. $ Give examples of linear operators $A:V\longrightarrow V$ satisfying (a) $A$ is an isomorphism but not the identity; (b) the dimension of the image of $A$ is equal to 1; (b) the dimension of the kernel of $A$ is equal to 1. Hint 1: try $V=\mathbf{R}^{3}$ first. Hint 2: use the basis.
6. Find the eigenvalues, the eigenvectors, and the bases of the eigenspaces of the matrix:

\begin{equation*} \left[ \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1% \end{array}% \right] . \end{equation*}

Solutions

Test 2:

• 1. $(A^m)^{-1} = (A^{-1})^m$ because $$(a^m)^{-1}=\frac{1}{a^m} = a^{-m} = (a^{-1})^m.$$

Proof is easy, exercise.

• 2. $B = \{1,x,x^2\}$, $D = \{2,x-x^2,x-1\}$, express in terms of $B$.

$$2 = 2 \cdot 1 = \left[ \begin{array}{} 2 \\ 0 \\ 0 \end{array} \right]$$

$$x-x^2 = 0 \cdot 1 + 1 \cdot x + (-1)x^2 = \left[ \begin{array}{} 0 \\ 1 \\ -1 \end{array} \right]$$

$$x-1 = -1 \cdot 1 + 1 \cdot x + 0 \cdot x^2 = \left[ \begin{array}{} -1 \\ 1 \\ 0 \end{array} \right]$$

Form a matrix from these columns.

• 3. ${\rm grad \hspace{3pt}}f(a) = \left( \frac{\partial f}{\partial x}(a), \frac{\partial f}{\partial y}(a) \right)$ is linear ($a$ fixed)

Use calculus; ${\rm grad \hspace{3pt}} \colon V \rightarrow {\bf R}^2$.

• 4. $$X \stackrel{f}{\rightarrow} Y \stackrel{g}{\rightarrow} Z$$ where $f$ and $g$ are onto.

Prove $g \circ f$ is onto if and only if for every $z \in Z$ there is $x \in X$ such that $(g \circ f)(x)=z$.

exists?:

$g$ is onto, so there is $y \in Y$ such that $g(y)=z$.

$f$ is onto, so there is $x \in X$ such that $f(x)=y$.

So $$(g \circ f)(x) = g(f(x)) = g(y) = z.$$

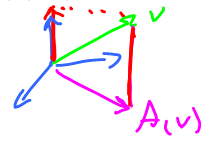
• 5. $V$ (abstract) vector space.
  • a) Let $A$ be a stretch: $A(v)=2v$.

Hint 2: use the basis

• • b) ${\rm dim \hspace{3pt} ker \hspace{3pt}}A=1$.

$A \colon {\bf R}^3 \rightarrow {\bf R}^3$ projection on $xy$-plane.

$$A(e_3)=0$$

$$A(e_1)=e_1$$

$$A(e_2)=e_2$$

Use $S$, the basis:

$A(e)=0$ for some $e \in S$

$A(v)=v$ for the rest of elements of $S$.

• • c)${\rm dim \hspace{3pt} im \hspace{3pt}}A=1$

$$A(e_1)=0$$

$$A(e_2)=0$$

$$A(e_3)=e_3$$

• 6. Eigenspaces?

Eigenvalues: $\lambda=0,1,2 \longleftarrow A = \left[ \begin{array}{} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right] \longrightarrow {\rm det}(\lambda I-A)=0$. (this implies $\lambda=0,1,2$.)

How do we find eigenvectors?

$Av=\lambda v$, solve for $v$.

$$\lambda = 1 \left[ \begin{array}{} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{} x \\ y \\ z \end{array} \right] = 1 \left[ \begin{array}{} x \\ y \\ z \end{array} \right] \rightarrow \left\{ \begin{array}{} x+z &= x \\ y &= y \\ x + z &= z \end{array} \right.$$

Therefore $x=z$ and $x=z=0$, $y$ is arbitrary.

The eigenspace is $\{(0,t,0) \colon t \in {\bf R}\}$. Basis $\{(0,1,0)\}$.