This site is being phased out.
Limits and continuity
Contents
- 1 Limits of functions: small scale trends
- 2 Limits under algebraic operations
- 3 Discontinuity: what to avoid
- 4 Continuity of transformations
- 5 Continuity under algebraic operations
- 6 The transcendental functions
- 7 Limits and continuity under compositions
- 8 Continuity of the inverse
- 9 More on limits and continuity
- 10 Global properties of continuous functions
- 11 Large-scale behavior and asymptotes
- 12 Limits and infinity
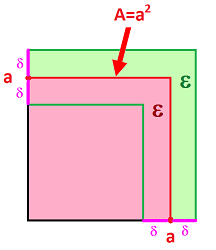
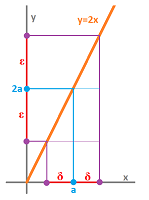
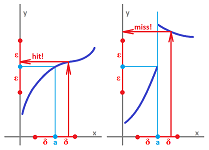
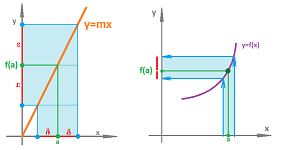
- 13 Continuity and accuracy
- 14 The $\varepsilon$-$\delta$ definition of limit
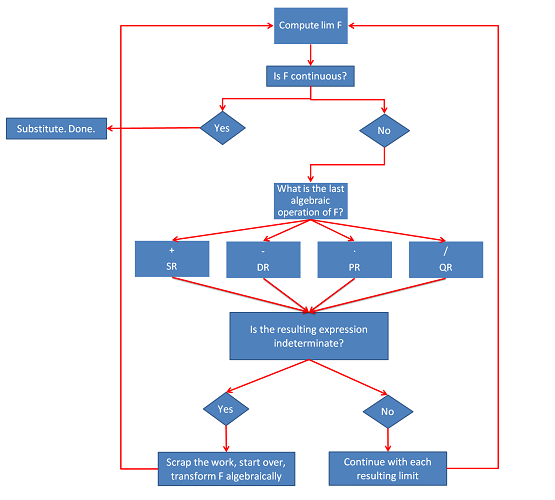
- 15 Flowchart for limit computation
Limits of functions: small scale trends
We now study small scale behavior of functions; we zoom in on a single point of the graph.
One of the most crucial properties of a function is the integrity of its graph: is there a break or a cut? For example, in order to study motion, we typically assume that to get from point $A$ to point $B$, we have to visit every location between $A$ and $B$.
If there is a jump in the graph of the function, it can't represent motion!
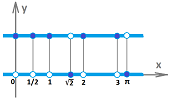
Thus, we want to understand what is happening to $y=f(x)$ when $x$ is in the vicinity of a chosen point $x=a$.
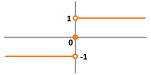
The tool with which we choose to study the behavior of a function around a point is a sequence converging to the point ($x_n\to a$). We “lift” these points from the $x$-axis to the graph of the function:
We then look for a possible long-term pattern of behavior of this new sequence. Do these points accumulate to another point on the graph? Since we already know that the $x$-coordinates of these points do accumulate (to $x=a$), the question becomes: what is happening to the $y$-coordinates?
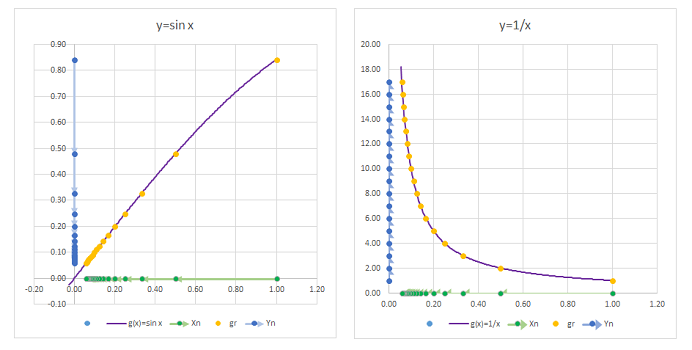
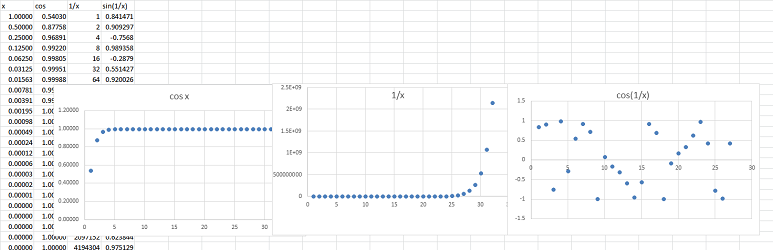
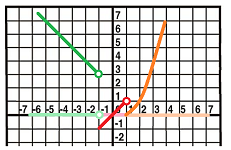
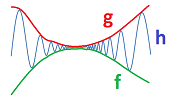
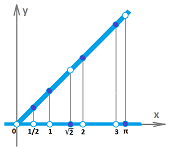
Example. Suppose we would like to study these three functions around the point $a=0$: $$f(x)=\cos x,\quad g(x)=\frac{1}{x},\quad h(x)=\sin (1/x).$$
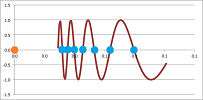
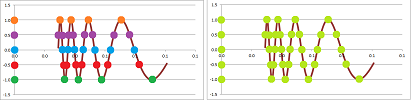
The reciprocal sequence is an appropriate choice: $$x_n=\frac{1}{n}\to 0.$$ Recall that the composition of any function and a sequence gives us a new sequence. We have then three, one for each function: $$a_n=\cos (1/n),\quad b_n=\frac{1}{1/n},\quad c_n=\sin\left( \frac{1}{1/n} \right).$$ This is how these sequences have been obtained, from the $x$-axis to the graph to the $y$-axis:
And this is what we discover about these new sequences when we explore them numerically:
Here we can see the following result for $n\to \infty$: $$a_n=\cos (1/n)\to 1,\quad b_n=n\to\infty,\quad c_n=\sin(n) \text{ diverges}.$$
Compare the results to the graphs of the functions:
The behaviors match! Our sequence was able to reveal the behavior of each function around $0$. $\square$
Thus, the initial idea of how to find what is happening to $y=f(x)$ as $x$ is approaching $a$ is to pick a sequence that approaches $a$, i.e., $x_n\to a$. Then we evaluate this limit of a new sequence that comes from substitution: $$\lim_{n\to\infty}f(x_n)=?$$
If we think of the sequence $x_n$ as a function, then we should interpret this substitution, $$y_n=f(x_n),$$ as the composition, as discussed in Chapter 5.
A single sequence might not be enough though!
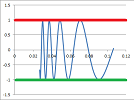
Example. Just observe the following failure of a single sequence to tell us what is going on with the function $\operatorname{sign}$ around $0$.
We try $x_n=-1/n$ and $x_n=1/n$: $$\lim_{n\to \infty} \operatorname{sign}(-1/n)=-1,\ \text{ but } \lim_{n\to \infty} \operatorname{sign}(1/n)=1,$$ as we approach $0$ from one direction at a time. The limits don't match! In fact, the result suggests that the limit of $\operatorname{sign}(x)$ simply doesn't exist at this point. $\square$
Example. Another failure is of the sequence $x_n=\frac{1}{\pi n}$ where $\frac{1}{n}$ succeeded: $$\lim_{n\to \infty} \sin\left( \frac{1}{1/n} \right) \text{ doesn't exist, but }\lim_{n\to \infty} \sin\frac{1}{x_n}=\lim_{n\to \infty} \sin(\pi n)=\lim_{n\to \infty}0=0.$$
$\square$
The answer is to try to substitute all sequences that converge to $a$ and ensure they all induce the same behavior from $f$.
Definition. The limit of a function $f$ at a point $x=a$ is defined to be the limit $$\lim_{n\to \infty} f(x_n)$$ considered for all sequences $x_n$ within the domain of $f$ excluding $a$ that converge to $a$, $$a\ne x_n\to a\ \text{ as } n\to \infty,$$ when all these limits exist and are equal to each other. In that case, we use the notation: $$\lim_{x\to a} f(x).$$ Otherwise, the limit does not exist.
Example. Take $f(x)=x^2$ at $a=0$. We test three sequences: $$x_n=\frac{1}{n},\quad y_n=-\frac{1}{n},\quad z_n=\frac{(-1)^n}{n} .$$ It doesn't matter: $$\lim_{x\to a} f(x_n)=\lim_{x\to a} f(y_n)=\lim_{x\to a} f(z_n)=\lim_{x\to 0} \frac{1}{n^2}=0.$$ $\square$
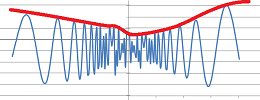
Example. As we have seen, this limit does not exist: $$\lim_{x\to 0} \sin \left( \frac{1}{x} \right)\ \text{ DNE.}$$ In fact, the values of this function start to fill the whole interval $[-1,1]$ as we approach $0$:
However, if we multiply this expression by $x$, the swings will start to diminish on the way to $0$:
We have a limit: $$\lim_{x\to 0} x\sin \left( \frac{1}{x} \right)=0.$$ $\square$
Example. Let's use the alternating reciprocal sequence for $y=\operatorname{sign}(x)$: $$x_n=(-1)^n\frac{1}{n}.$$ Then, $$\operatorname{sign}(x_n)=\begin{cases} 1&\text{ if } x \text{ is even},\\ -1&\text{ if } x \text{ is odd}. \end{cases}$$ This sequence is divergent. Therefore, the definition fails, and $\lim_{x\to 0} \operatorname{sign}(x)$ doesn't exist.
Another way to come to this conclusion is to concentrate on one side at a time: $$\begin{array}{ll} \lim_{n\to \infty} \operatorname{sign}\left( -\frac{1}{n} \right)&=\lim_{n\to \infty}-1&=-1 ,\\ \lim_{n\to \infty} \operatorname{sign} \left( \frac{1}{n} \right)&=\lim_{n\to \infty} 1&=1. \end{array}$$ The two limits are different, the definition fails, and that's why $\lim_{x\to 0} \operatorname{sign}(x)$ doesn't exist. $\square$
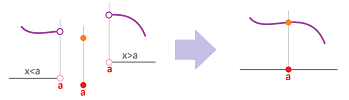
However, the last result also reveals that the behavior of $y=\operatorname{sign}(x)$ on the left and on the right, when considered separately, is very regular. Indeed, we can choose any sequences and, as long as they stay on one side of $0$, we have the same conclusion:
- if $x_n\to 0$ and $x_n<0$ for all $n$, then $\lim_{n\to \infty} \operatorname{sign}(x_n)=-1$, and
- if $x_n\to 0$ and $x_n>0$ for all $n$, then $\lim_{n\to \infty} \operatorname{sign}(x_n)=1$.
To take advantage of this insight, we can imagine that either the part of the graph to the left of $x=a$ disappears or the part to the right:
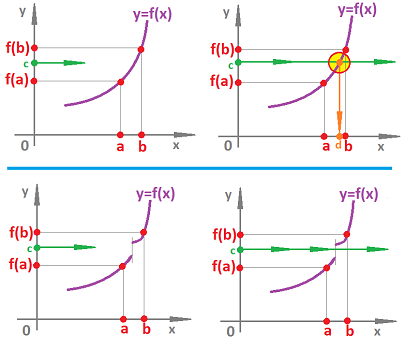
Definition. The limit from the left of a function $f$ at a point $x=a$ is defined to be the same limit, $\lim_{n\to \infty} f(x_n)$ but only considered for sequences $x_n$ with $$x_n\to a\ \text{ as } n\to \infty,\ \ \text{ and } x_n<a\ \text{ for all } n,$$ when all these limits exist and are equal to each other. The limit from the right of a function $f$ at a point $x=a$ is defined to be the same limit, $\lim_{n\to \infty} f(x_n)$ but only considered for sequences $x_n$ with $$x_n\to a\ \text{ as } n\to \infty,\ \ \text{ and } x_n>a\ \text{ for all } n,$$ when all these limits exist and are equal to each other. In that case, we use the notation: $$\text{left: }\ \lim_{x\to a^-} f(x)\quad \text{ or } \quad \lim_{x\nearrow a} f(x),$$ and $$\text{right: }\ \lim_{x\to a^+} f(x)\quad \text{ or }\quad \lim_{x\searrow a} f(x),$$ respectively. Otherwise, we say that the limit does not exist. Collectively, the two are called one-sided limits.
In other words, one-sided limits are the limits of the function restricted to an interval to the left or to the right of the point.
For the “two-sided” limit, the question becomes, do the two -- left and right -- limits match?
Theorem. The limit of a function $f$ at a point $x=a$ exists if and only if the limits from the left and from the right of $f$ at $x=a$ exist and are equal to each other. Then $$\lim_{x\to a} f(x)=\lim_{x\to a^+} f(x)=\lim_{x\to a^-} f(x).$$
Proof. The existence of this limit means that $\lim_{n\to \infty} f(x_n)$ exists for any sequence $x_n\to a$ and is the same. In particular, this is true for the sequences limited to the ones all larger than $a$ and all smaller than $a$. The proof of the converse is omitted. $\blacksquare$
Example. Let's plot the graph of this function: $$ f(x) = \begin{cases} 2 - x & \text{ if } x < -1, \\ x & \text{ if } -1 < x < 1, \\ (x - 1)^{2} & \text{ if } x >1. \end{cases} $$ This is the initial data and three points to plot: $$ \begin{aligned} (1-1)^{2} & = 0, \\ (2-1)^{2} & = 1, \\ (3-1)^{2} & = 4. \end{aligned} $$ Also, $\lim\limits_{x \to a} f(x)$ exists for all $a$ except $a = -1,1$. Our computations also reveal: $$ \begin{array}{ll} \lim_{x \to -1^{-}} f(x) & = 3, &\lim_{x \to -1^{+}} f(x) & = -1 ;\\ \lim_{x \to 1^{-}} f(x) & = 1, &\lim_{x \to 1^{+}} f(x) & = 0. \end{array} $$ Then this is the graph made of three branches, one for each different formula:
$\square$
This example was about interpreting the graph in terms of limits. Now, the other way around: from limits to graphs.
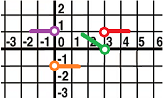
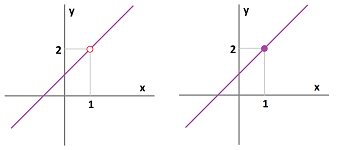
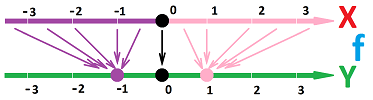
Example. Given this information about $f$, plot its graph: $$\begin{alignat}{3} \lim_{x \to 0^{-}} f(x) & = 1, & \quad \lim_{x \to 0^{+}} f(x) &= -1, & \quad f(0) & \text{ undefined}, \\ \lim_{x \to 2^{-}} f(x) &= 0, &\quad \lim_{x \to 2^{+}} f(x) & = 1, &\quad f(2) &= 1. \end{alignat} $$ We re-write the one-sided limits:
- as $x \to 0^{-}$, we have: $y \to 1$;
- as $x \to 0^{+}$, we have: $y \to -1$;
- as $x\to 2^{-}$, we have: $y \to 0$;
- as $x\to 2^{+}$, we have: $y \to 1$.
Then we plot the results below concentrating on the behavior of $f$ close to these points:
$\square$
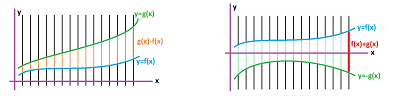
Example. Is it possible that $\lim\limits_{x \to a} (f(x)+g(x))$ exists, even though $\lim\limits_{x \to a} f(x)$ and $\lim\limits_{x \to a} g(x)$ do not? In other words, can the addition $f + g$ cancel their irregular behavior? Of course; just pick $g = -f$. Then $f + g = 0$, so $\lim\limits_{x \to a} (f + g) = 0$. For a specific example, we can take $f(x) = \dfrac{1}{x}$ and $a = 0$. The $\lim\limits_{x \to 0} \dfrac{1}{x}$ does not exist. Neither does, $\lim\limits_{x \to 0} \left(-\dfrac{1}{x}\right)$. But $$ \lim_{x \to 0} \left[ \dfrac{1}{x} + \left(-\dfrac{1}{x} \right) \right] = \lim_{x \to 0} 0 = 0. $$ $\square$
Theorem. If $\lim\limits_{x \to a} f(x)$ exists but $\lim_{x \to a} g(x)$ does not, then $\lim\limits_{x \to a} (f(x) +g(x))$ does not exist.
As we know, the limit of a sequence is fully determined by its tail. Therefore, the limit of a function at $a$ is fully determined by the tail of the sequence $f(x_n)$ when $x_n\to a$. It follows then that only the behavior of $f$ in the vicinity, no matter how small, of $a$ affects the value (and the existence) of the limit $\lim_{x\to a} f(x)$.
Theorem (Localization). Suppose two functions $f$ and $g$ coincide in the vicinity of point $a$: $$f(x)=g(x) \quad \text{ for all } a-\varepsilon <x <a+\varepsilon,\ x\ne a,$$ for some $\varepsilon >0$. Then, their limits at $a$ coincide too: $$\lim_{x\to a} f(x) =\lim_{x\to a} g(x).$$
Exercise. Restate the theorem in terms of restrictions of functions.
Exercise. State an analog of the theorem for one-sided limits.
Limits under algebraic operations
We will use the algebraic properties of the limits of sequences to prove virtually identical facts about limits of functions.
Let's re-write the main algebraic properties using the alternative notation.
Theorem (Algebra of Limits of Sequences). Suppose $a_n\to a$ and $b_n\to b$. Then $$\begin{array}{|ll|ll|} \hline \text{SR: }& a_n + b_n\to a + b& \text{CMR: }& c\cdot a_n\to ca& \text{ for any real }c\\ \text{PR: }& a_n \cdot b_n\to ab& \text{QR: }& a_n/b_n\to a/b &\text{ provided }b\ne 0\\ \hline \end{array}$$
Presented verbally, these rules have these abbreviated versions:
- the limit of the sum is the sum of the limits;
- the limit of the difference is the difference of the limits;
- the limit of the product is the product of the limits;
- the limit of the quotient is the quotient of the limits (as long as the one of the denominator isn't zero).
Each property is matched by its analog for functions. Furthermore, there are analogs for the one-sided limits. In fact, we will see analogs of some of these rules for numerous new concepts to appear in the forthcoming chapters.
Theorem (Algebra of Limits of Functions). Suppose $f(x)\to F$ and $g(x)\to G$ as $x\to a$ (or $x\to a^-$ or $x\to a^+$). Then $$\begin{array}{|ll|ll|} \hline \text{SR: }& f(x)+g(x)\to F+G & \text{CMR: }& c\cdot f(x)\to cF& \text{ for any real }c\\ \text{PR: }& f(x)\cdot g(x)\to FG& \text{QR: }& f(x)/g(x)\to F/G &\text{ provided }G\ne 0\\ \hline \end{array}$$
Let's consider them one by one.
Now, limits behave well with respect to the usual arithmetic operations.
Theorem (Sum Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their sum, $f(x) \pm g(x)$, and the limit of the sum is equal to the sum of the limits: $$\lim_{x\to a} (f(x) + g(x)) = \lim_{x\to a} f(x) + \lim_{x\to a} g(x).$$
Proof. For any sequence $x_n\to a$, we have by SR: $$\lim_{x\to a} (f(x) + g(x)) = \lim_{n\to \infty} (f(x_n)+g(x_n)) = \lim_{n\to \infty} f(x_n)+\lim_{n\to \infty} g(x_n).$$ $\blacksquare$
In the case of infinite limits, we follow the rules of the algebra of infinities as in Chapter 5: $$\begin{array}{lll} \text{number } &+& (+\infty)&=+\infty;\\ \text{number } &+& (-\infty)&=-\infty;\\ +\infty &+& (+\infty)&=+\infty\;\ -\infty &+& (-\infty)&=-\infty.\\ \end{array}$$
The proofs of the rest of the properties are identical.
Theorem (Constant Multiple Rule). If the limit at $a$ of function $f(x)$ exists then so does that of its multiple, $c f(x)$, and the limit of the multiple is equal to the multiple of the limit: $$\lim_{x\to a} c f(x) = c \cdot \lim_{x\to a} f(x).$$
Theorem (Product Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their product, $f(x) \cdot g(x)$, and the limit of the product is equal to the product of the limits: $$\lim_{x\to a} (f(x) \cdot g(x)) = (\lim_{x\to a} f(x))\cdot( \lim_{x\to a} g(x)).$$
Let's set $g(x)=c$ in PR and use CR, then $$\lim_{x\to a} c f(x)= \lim_{x\to a} (f(x) \cdot g(x)) = c\cdot( \lim_{x\to a} g(x)).$$ Then CMR follows. Even though CMR is absorbed into PR, the former is simpler and easier to use.
Theorem (Quotient Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their ratio, $f(x) / g(x)$, provided $\lim_{x\to a} g(x) \ne 0$, and the limit of the ratio is equal to the ratio of the limits: $$\lim_{x\to a} \left(\frac{f(x)}{g(x)}\right) = \frac{\lim\limits_{x\to a} f(x)}{\lim\limits_{x\to a} g(x)}.$$
We can say that the limit sign is “distributed” over these algebraic operations.
The main building blocks are these two functions -- the constant function and the identity function -- with simple limits.
Theorem (Constant). For any real $c$, the following limit exists at any point $a$: $$\lim_{x\to a} c = c.$$
Proof. For any sequence $x_n\to a$, we have $$\lim_{x\to a} c = \lim_{n\to \infty} c = c.$$ $\blacksquare$
Theorem (Identity). The following limit exists at any point $a$: $$\lim_{x\to a} x = a.$$
Proof. For any sequence $x_n\to a$, we have $$\lim_{x\to a} x = \lim_{n\to \infty} x_n = a.$$ $\blacksquare$
Any polynomial can be built from $x$ and constants by multiplication and addition. Therefore, the first five theorems allow us to compute the limits of all polynomials.
Example. Let $$f(x)=x^3+3x^2-7x+8.$$ What is its limit as $x\to 1$? The computation is straightforward, but every step has to be justified with the rules above.
To understand which rules to apply first, observe that the last operation is addition. We use SR first: $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1} (x^3+3x^2-7x+8) &\text{ ...then by SR, we have...}\\ &=\lim_{x\to 1} x^3+\lim_{x\to 1}3x^2-\lim_{x\to 1}7x+\lim_{x\to 1}8 &\text{ ...then using }\\ &\quad\quad \text{ PR, } \quad\quad \text{ CMR, } \quad \text{ CMR, } \quad \text{ CR}, &\text{ we have... }\\ &=\lim_{x\to 1} x \cdot\lim_{x\to 1} x^2+3\lim_{x\to 1}x^2-7\lim_{x\to 1}x+8 \quad&\text{ ...then by IR, we have...}\\ &=1\cdot\lim_{x\to 1} x^2+3\lim_{x\to 1}x^2-7\cdot 1+8 \quad&\text{ ...then by PR and IR, we have...}\\ &=1 \cdot 1 +3 \cdot 1 -7+8\\ &=5. \end{array}$$ $\square$
With this complex argument, it is easy to miss the simple fact that the limit of this function happens to be equal to its value: $$\lim_{x\to 1}f(x)=\lim_{x\to 1} (x^3+3x^2-7x+8)=x^3+3x^2-7x+8\Big|_{x=1}=1^3+3\cdot 1^2-7\cdot 1+8 =5.$$ The idea is confirmed by the plot:
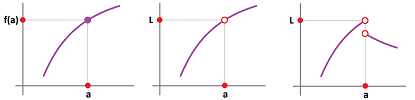
Definition. A function $f$ is called continuous at point $a$ if
- $f(x)$ is defined at $x=a$,
- the limit of $f$ exists at $a$, and
- the two are equal to each other:
$$\lim_{x\to a}f(x)=f(a).$$
Thus, the limits of continuous functions can be found by substitution.
Equivalently, a function $f$ is continuous at $a$ if $$\lim_{n\to \infty}f(x_n)=f(a),$$ for any sequence $x_n\to a$.
As we shall see, all polynomials are continuous. Now an example of a rational function...
Example. Let's find the limit at $2$ of $$f(x)=\frac{x+1}{x-1}.$$ Again, we look at the last operation of the function. It is division, so we use QR first: $$\begin{array}{lll} \lim_{x\to 2}f(x)&=\lim_{x\to 2}\frac{x+1}{x-1}&\text{...we now justify QR by observing that }\\ && \lim_{x\to 2}(x-1)=1\ne 0, \text{ then...}\\ &=\frac{\lim_{x\to 2}(x+1)}{\lim_{x\to 2}(x-1)}\\ &=\frac{3}{1}\\ &=3. \end{array}$$ $\square$
Example. Let's find the limit at $1$ of the function $$f(x)=\frac{x^2-1}{x-1}.$$ Since the last operation is division, so are supposed to use QR first. However, the limit of the denominator is $0$: $$\lim_{x\to 1}(x-1)=0.$$ Then, QR is inapplicable. But then all other rules of limits are also inapplicable!
A closer look reveals that things are even worse; both the numerator and the denominator go to $0$ as $x$ goes to $1$. An attempt to apply QR -- over these objections -- would result in an indeterminate expression: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2-1}{x-1}& \ra{???}& \frac{0}{0}\text{ as } x\to 1.\end{array}$$ This doesn't mean that the limit doesn't exist; we just need to get rid of the indeterminacy. The answer is algebra.
We factor the numerator and then cancel the denominator (thereby circumventing the need for QR): $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1}\frac{x^2-1}{x-1}\\ &=\lim_{x\to 1}\frac{(x-1)(x+1)}{x-1}\\ &=\lim_{x\to 1}(x+1) \\ &=2. \end{array}$$ The cancellation is justified by the fact that $x$ tends to $1$ but never reaches it. $\square$
Example. Let's consider more examples of how trying to apply the laws of limits without verifying their conditions could lead to indeterminate expressions. We choose a few algebraically trivial situations.
First, for $x\to 0$, a misapplication of QR leads to the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2}{x}& \ra{???}& \frac{0}{0},&\text{ instead of }\frac{x^2}{x}=x\to 0.\end{array}$$ We now discover how the same indeterminate expression has a different outcome: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x}{x^2}& \ra{???}& \frac{0}{0},&\text{ instead of }\frac{x}{x^2}=\frac{1}{x}\to \infty.\end{array}$$ And another one: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{2x}{x}& \ra{???}& \frac{0}{0},&\text{ instead of }\frac{2x}{x}=2\to 2.\end{array}$$ $\square$
The answer to a limit problem can't be “It's indeterminate!”. We have to determine it.
Example. Now, there are other kinds of indeterminate expressions. For $x\to \infty$, a misapplication of QR leads to the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2}{x}& \ra{???}& \frac{\infty}{\infty},&\text{ instead of }\frac{x^2}{x}=x\to \infty.\end{array}$$ The same indeterminate expression has a different outcome: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x}{x^2}& \ra{???}& \frac{\infty}{\infty},&\text{ instead of }\frac{x}{x^2}=\frac{1}{x}\to 0.\end{array}$$
Finally, we see how indeterminate expressions appear under SR instead of QR. For $x\to \infty$, we have the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll} (x+1)-x & \ra{???}& \infty -\infty,&\text{ instead of }(x+1)-x =1.\end{array}$$ $\square$
Example. Compute $$\lim\limits_{x \to 0} \dfrac{\sqrt{x^{2} + 9} - 3}{x^{2}}.$$ If we mindlessly substitute $x=0$, we get $0/0$... What does it mean? It means: $$\begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}$$ STOP! Erase everything and do algebra. The goal is to cancel the denominator. The trick is to multiply by the conjugate, $\sqrt{x^{2} + 9} + 3$, of the numerator in order to “rationalize” it. Then we have: $$ \begin{aligned} \lim_{x \to 0} \dfrac{\sqrt{x^{2} + 9} - 3}{x^{2}} & = \lim_{x \to 0} \dfrac{(\sqrt{x^{2} + 9} - 3)\cdot (\sqrt{x^{2} + 9} + 3)}{x^{2}\cdot (\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{(x^{2} + 9) - 3^{2}}{x^{2}(\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{x^{2}}{x^{2}(\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{1}{\sqrt{x^{2} + 9} + 3} \\ & = \dfrac{1}{\sqrt{0 + 9} + 3} \\ &= \dfrac{1}{6}. \end{aligned} $$ At the end, QR applies because the limit in the denominator exists and is not $0$. $\square$
Below, we re-state these famous limits for sequences from Chapter 5 as limits for functions: $$\lim_{n\to \infty} \frac{\sin x_n}{x_n} =1,\qquad \lim_{n\to \infty} \frac{1 - \cos x_n}{x_n} = 0,$$ for any sequence $x_n\to 0$.
Theorem (Famous limits). $$\begin{array}{ll} \lim_{x\to 0} \frac{\sin x}{x} =1;& \lim_{x\to 0} \frac{1 - \cos x}{x} = 0. \end{array}$$
They would produce indeterminate expressions if we tried to apply the rules of limits without checking their conditions first.
Instead of concentrating on how $x$ is approaching $a$, we can look at how far we step away from $a$. We consider the increment, i.e., the difference $h$ between the two. Thus, we replace $$x\to a \text{ with } h=x-a\to 0.$$
Then we re-write the limit $\lim_{x \to a} f(x)$ by substitution $h = x - a$, as follows.
Theorem (Alternative formula for limit). The limit of a function $f$ at $a$ is equal to $L$ if and only if $$\lim_{h \to 0} f(a + h) = L.$$
This will make our computations look different...
Example. Let's use the theorem to take another look at the following limit: $$\begin{array}{lll} \lim_{x \to 1} \frac{x^2-1}{x-1}&=\lim_{h \to 0} \frac{(1+h)^2-1}{(1+h)-1}&\text{ ...by the theorem,}\\ &=\lim_{h \to 0} \frac{1+2h+h^2-1}{1+h-1}&\text{ ...expand,}\\ &=\lim_{h \to 0} \frac{2h+h^2}{h}&\text{ ...simplify,}\\ &=\lim_{h \to 0} (2+h)&\text{ ...divide,}\\ &=2+h\bigg|_{h=0}&\text{ ...substitute,}\\ &=2. \end{array}$$ This time, we didn't have to do any factoring! $\square$
As we see, this substitution might make the algebra simpler.
Exercise. Use the theorem to compute: $$\lim_{x \to 1} \frac{x^3-1}{x-1}.$$
Just as with sequences, we can represent the Sum Rule as a diagram: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccc} f,g&\ra{\lim}&F,G\\ \ \da{+}&SR &\ \da{+}\\ f+g & \ra{\lim}&\lim(f+g)=F+G \end{array} $$ In the diagram, we start with a pair of functions at the top left and then we proceed in two ways:
- right: take the limit of either, then down: add the results; or
- down: add them, then right: take the limit of the result.
The result is the same! For the Product Rule and the Quotient Rule, we just replace “$+$” with “$\cdot$” and “$\div$” respectively.
Discontinuity: what to avoid
If one stands at the edge of a cliff, one small step may lead to catastrophic consequences.
Standing off the edge will not. One can capture this phenomenon with the graph of this function: $$f(x)=\begin{cases} 1&\text{ if } x\le 0;\\ 0&\text{ if } x> 0. \end{cases}$$
In Chapters 6 - 10, we will study functions on a small scale. That is why the functions that may produce a dramatically different output in response to a small change in the input will not initially be a subject of our study. In Chapter 11 and 12, we will study functions on a large scale and these functions won't present a problem.
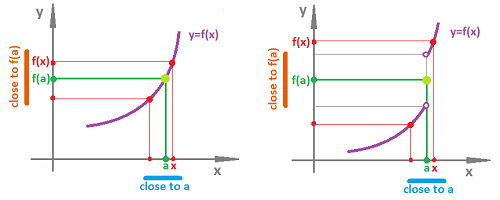
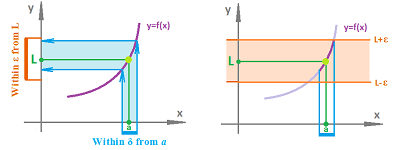
What is the opposite of these “poorly behaved” functions? This is what we mean by a continuous dependence of $y$ on $x$ under function $f$:
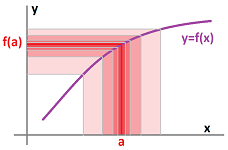
- a small deviation of $x$ from $a$ produces a small deviation of $y=f(x)$ from $f(a)$:
The idea is visualized below:
Such dependencies are ubiquitous in nature:
- the location of a moving object continuously depends on time,
- the pressure in a closed container continuously depends on the temperature,
- the air resistance continuously depends on the velocity of the moving object, etc.
It is our goal to develop this idea in full rigor and to make sure that our mathematical tools match the perceived reality.
One of the informal ideas about continuity is that the graph of such a function is “made of a single piece”. We think of the graph as a rope:
Even though it look intact, there may be an invisible cut that allow us to pull it apart.
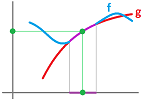
Example. Consider these two functions: $$f(x)=\frac{x^2-1}{x-1} \text{ and } g(x)=x+1.$$ The limit of the former is found by this computation: $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1}\frac{x^2-1}{x-1}\qquad \to \frac{0}{0}? \qquad\begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}\\ &=\lim_{x\to 1}\frac{(x-1)(x+1)}{x-1}\\ &=\lim_{x\to 1}(x+1) \\ &=2. \end{array}$$ At the end, we use the fact that $x+1$ is continuous to apply a direct substitution. That's the only thing we need for the other limit: $$\lim_{x\to 1}g(x)=\lim_{x\to 1}(x+1)=x+1\Big|_{x=1}=1+1=2.$$
The two functions are almost the same and the difference is seen in their graphs below. To emphasize the difference we use a little circle to indicate the missing point:
There is only one point missing from the former graph. However, if we think of the graph of a function as a rope, we realize that the former graph consists of two separate pieces! Even though the cut is invisibly thin, we can pull the pieces apart. The latter graph is a single piece. It is indeed “continuous”. A light breeze would only move the latter but blow apart the former:
$\square$
The discontinuous graph in the last example was easy to “repair” (glue, solder, weld, etc.) by adding a single point. There are other, more extreme, cases of discontinuity. They cannot be fixed.
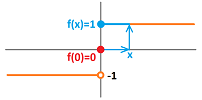
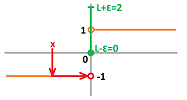
Example. The sign function $f(x)=\operatorname{sign}(x)$ has a visible gap at $x=0$:
This example shows how the idea of continuous dependence of $y$ on $x$ fails: starting with $x=0$, even a tiniest deviation of $x$, say, $x=.0001$, produces a jump in $y$ from $\operatorname{sign}(0)=0$ to $\operatorname{sign}(.0001)=1$. $\square$
Example. A more general view of the “jump discontinuity” is shown below:
These $x$'s that are “close” to $a$ don't all end up “close” to $f(a)$. $\square$
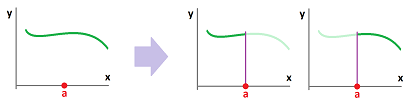
The examples teach us a lesson. Given a function $f$ and a point $a$, where $f$ is defined, the graph of $f$ consists of three parts:
- 1. the part of the graph of $f$ with $x<a$,
- 2. the part of the graph of $f$ with $x=a$ (one point), and
- 3. the part of the graph of $f$ with $x>a$.
For this function to be continuous, these three parts (the two pieces of the rope and a drop of glue) have to fit together:
We put this idea in the form of a theorem that relies on the concept of a one-sided limit.
Theorem. A function $f$ is continuous at $x=a$ if and only if $f$ is defined at $a$, the two one-sided limits exist and both equal to the value of the function at $a$; $$\lim_{x\to a^-}f(x)=f(a)=\lim_{x\to a^+}f(x).$$
Where do discontinuous functions come from?
We can observe them in nature around us:
- walking continuously -- until falling off a cliff,
- increasing the pressure continuously in a closed container -- until it explodes,
- increasing the temperature continuously of a piece of ice -- until it melts.
Examples of discontinuity routinely come from human affairs because the outcomes are often designed to be discrete: Yes or No, all or nothing, etc.
Example (grades). Let's consider possible outcomes in a university environment. We start with pass/fail. The outcome depends on your total (or average) score. A threshold is typically assigned: if the score is above it, you pass, otherwise you fail no matter how close you are. That's discontinuity!
Using letter grades relieve this somewhat, but there are still thresholds! They will remain even if we choose to use $A-$, $B+$, etc.
Generally, there are only a few possible outputs (the letter grades) but the input (the score) is arbitrary. To try to plot the graph of how the outcomes depend on the score, we show above the lines that must contain the graph of the function. There cannot be a continuous function with such a graph. $\square$
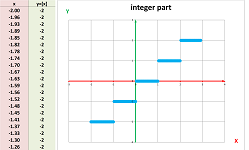
Example. A pair of useful discontinuous functions are the following two. First is the the integer part:
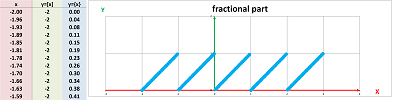
The second is the fractional part:
$\square$
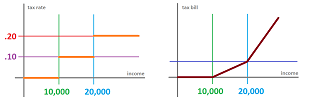
Example (taxes). A special care has to be taken in order to ensure continuity. Let's recall an example from Chapter 3. Hypothetically, suppose the tax code says about these three brackets of income:
- if your income is less than $\$ 10000$, there is no income tax;
- if your income is between $\$ 10000$ and $\$ 20000 $, the tax rate is $10\%$;
- if your income is over $\$ 20000$, the tax rate is $20\%$.
We can express this algebraically. Suppose $x$ is the income and $y = f(x)$ is the tax rate, then $$f(x) = \begin{cases} 0 & \text{if } x \le 10000; \\ .10 & \text{if } 10000 < x \le 20000; \\ .20 & \text{if } 20000 <x. \end{cases}$$ The function is, of course, discontinuous (left):
We see why this is a problem once we try to apply it directly. Imagine that your income has risen from $\$10,000$ to $\$10,001$, but your tax bill has risen from $\$0$ to $\$1,000$! How do we fix this? The principle we want to follow here is that a “small” change in the income will cause only a “small” change in the tax bill. This requirement is satisfied as long as the income stays within the brackets. The issue arises only at the transition points and can be addressed in the way shown on right. The interpretation of the result is possible if we understand the law correctly. The tax rate is marginal, i.e., it is the tax rate applied to the part of the income that lies within the bracket and these three numbers are meant to be added together to produce your tax bill (or tax liability). This is the formula for the tax bill as a function of income: $$g(x) = \begin{cases} 0 & \text{if } x < 10000; \\ .10\cdot (x-10000) & \text{if } 10000 < x \le 20000; \\ .10\cdot (x-10000)+.20\cdot (x-20000) & \text{if } 20000 <x. \end{cases}$$ The function is continuous. $\square$
Exercise. Prove the formula above as well as the continuity of the function.
Even more extreme examples are below.
Example. The reciprocal function $g(x)=1/x$ has an infinite gap at $x=0$:
Here, if the deviations of $x$ from $0$ differ in sign, the jump in $y$ may be very large: from $\frac{1}{-.0001}=-10000$ to $\frac{1}{.0001}=10000$. $\square$
Example. The sine of the reciprocal $g(x)=\sin \left( 1/x \right)$ oscillates infinitely many times as we approach $0$:
Here, a deviation of $x$ from $0$ may unpredictably produce any number between $-1$ and $1$. Then, as we know, the limit of this function at $0$ does not exist. Therefore, the function cannot possibly be continuous at $0$ according to the definition. To appreciate this conclusion from the geometric point of view, it is impossible to attach this graph to a single point on the $y$-axis no matter what that point may be.
In the meantime, the function $h(x)=x\sin \left( 1/x \right)$ also oscillates infinitely many times as we approach $0$, yet, because the magnitude of these oscillations decreases, the limit exists (it's $0$!):
Does this make the function continuous? No, there is still a point missing at $0$. In other words, the two oscillating branches are detached. Let's glue them together. We simply define a new function: $$f(x)=\begin{cases} x\sin \left( 1/x \right)&\text{ if } x\ne 0;\\ 0&\text{ if } x= 0. \end{cases}$$ $\square$
Example (nowhere). The Dirichlet function is nowhere continuous! It is defined by: $$I_Q(x)=\begin{cases} 1 &\text{ if }x \text{ is a rational number},\\ 0 &\text{ if }x \text{ is an irrational number}. \end{cases}$$ In an attempt to plot its graph, we can only draw two horizontal lines and then simply point out some of the missing points in either:
If we were to plot all points, we'd have what looks like two complete straight lines. However, a light breeze would blow them apart:
$\square$
Continuity of transformations
An abstract function $y=f(x)$ given to us without any prior background may be supplied with a tangible representation:
- 1. we think of the function as if it represents motion: $x$ time, $y$ location;
- 2. we plot the graph of the function on a piece of paper;
- 3. we think of the function as a transformation of the real line.
Let's review the last point of view on function from Chapter 3: numerical functions are transformations of the real number line... and vice versa.
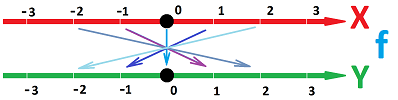
We represent a numerical function as correspondence between the $x$ and the $y$-axis (in contrast to the graph they are parallel instead of perpendicular to each other):
The arrows tell us what happens to each number but they also suggest what happens to the whole $x$-axis.
The function $$y=f(x)=x+k$$ shifts the $x$-axis in the positive direction when $k>0$ and in the negative direction when $k<0$.
Next, the function $$y=-x$$ takes the $x$-axis with at two spots nd then bring those two points to the assigned locations on the $y$-axis.
These two transformations don't distort the line and are called motions.
They are continuous!
A fold of a piece of wire:
This is the absolute value function, $y=|x|$!
Another type of transformation is a stretch, $$y=f(x)=x\cdot k,$$ of a rubber string. We grab it by the ends and pull them apart:
This is indeed a uniform stretch because the distance between any two points doubles.
We understand “stretched by a factor $k$” as “shrunk by a factor $1/k$”.
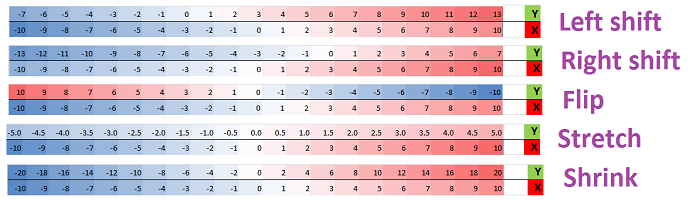
This is a combination of shifting, stretching, and shrinking:
We will often color the numbers according to their values. This is the summary of the functions we have considered:
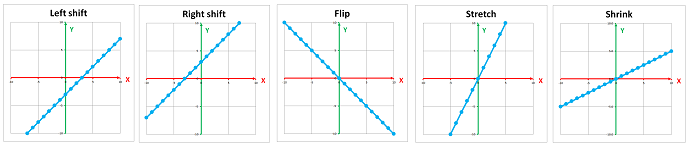
We also plot the graphs of these functions below:
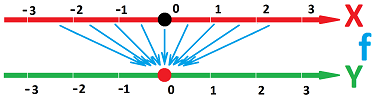
A constant functions, $f(x)=k$, is a collapse.
It shrinks to a single point.
The transformation of the domain into the codomain performed by the function can be seen in what happens to its graph:
First, we take the $x$-axis as if it is a rope and lift it vertically to the graph of the function and, second, we push it horizontally to the $y$-axis.
A transformation can tear this rope. That's discontinuity!
The sign function collapses the $x$-axis to three different points on the $y$-axis:
Exercise. Discuss the continuity of the integer value function.
Continuity under algebraic operations
With the apparent abundance of discontinuous functions, now the good news:
- a typical function we encounter is continuous at every point of its domain.
Of course, it can't be continuous outside. From all the functions we have seen so far, only a few piece-wise defined functions have been exceptions, especially the sign function and the integer value function.
We prove continuity of a function by showing (and later using many times) the fact that its limit is evaluated by substitution: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{|c|}\hline\quad \lim_{x\to a}F(x)=F(a) \quad \\ \hline\end{array} \text{ or } \begin{array}{|c|}\hline\quad F(x)\to F(a) \text{ as } x\to a.\quad \\ \hline\end{array} $$
Theorem.
- Every polynomial is continuous at every point.
- Every rational function is continuous at every point where it is defined.
The theorem follows from the following algebraic result.
Theorem. Suppose $f$ and $g$ are continuous at $x=a$. Then so are the following functions:
- 1. (SR) $f\pm g$,
- 2. (CMR) $c\cdot f$ for any real $c$,
- 3. (PR) $f \cdot g$, and
- 4. (QR) $f/g$ provided $g(a)\ne 0$.
Proof. For SR, we try to evaluate the limit of the sum at $a$ as follows: $$\begin{array}{lll} \lim_{x\to a} \big[ (f+g)(x) \big] &=\lim_{x\to a} \big[ f(x)+ g(x) \big] & \text{ ...then by SR for limits...}\\ &=\lim_{x\to a} f(x)+ \lim_{x\to a} g(x) &\text{ ...then by continuity...}\\ &=f(a)+g(a)\\ &=(f+g)(a). \end{array}$$ Therefore, the limit if $f+g$ is the value of the function; hence, it is continuous by the definition. Next, CMR, PR, and QR are proved with CMR, PR, and QR for limits, respectively. $\square$
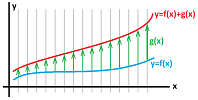
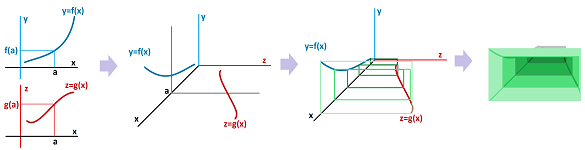
In SR, $g$ serves as a push of the graph of $f$. The picture below is meant to illustrate that idea. There is a rope, $f$, on the ground and there is also wind, $g$. Then, the wind, non-uniformly but continuously, blows the rope forward:
We can say that if the floor and the ceiling represented by $f$ and $g$ respectively of a tunnel are changing continuously then so is its height, which is $g-f$:
Or, if the floor and the ceiling ($f$ and $-g$) of a tunnel are changing continuously then so is its height ($g+f$). Thus, if there are no bumps in the floor and no bumps in the ceiling, you won't (suddenly) bump your head as you walk.
In CMR, $c$ is the magnitude of a vertical stretch/shrink of the rubber sheet that has the graph of $f$ drawn on it:
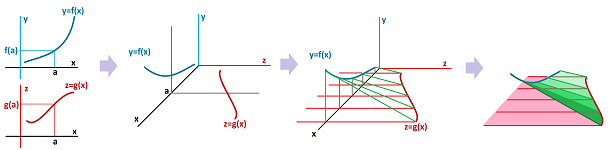
In PR, we say that if the width and the height ($f$ and $g$) of a rectangle are changing continuously then so is its area ($f\cdot g$):
In QR, we say that if the width and the height ($f$ and $g$) of a triangle are changing continuously then so is the tangent of its base angle ($f/g$):
The last one stands out with the extra restriction that the denominator isn't zero -- but only at the point $a$ itself. For example, $\frac{1}{x-1}$ is continuous at $x=0$; the fact that it is undefined at $1$ is irrelevant.
An abbreviated version of the theorem reads as follows.
Theorem. The sum, the difference, the product, and the ratio of two continuous functions is continuous (on its domain).
To justify our conclusion about the continuity of polynomials, let's consider a general representation of an $n$th degree polynomial: $$a_0+a_1x+a_2x^2+...+a_{n-1}x+a_nx^n.$$ Then we follow the following sequence of conclusions: $$\begin{array}{lrrrrr} \text{these are continuous: }&1&,&x&,&x&,&...&&x&,&x&;\\ \text{these are too by PR: }&1&,&x&,&x^2&,&...&&x^{n-1}&,&x^n&;\\ \text{these too by CMR: }&a_0&,&a_1x&,&a_2x^2&,&...&&a_{n-1}x^{n-1}&,&a_nx^n&;\\ \text{this is continuous by SR: }&a_0&+&a_1x&+&a_2x^2&+&...&+&a_{n-1}x^{n-1}&+&a_nx^n&. \end{array}$$ We also conclude that the graph of a polynomials consists of a single piece.
Once the continuity of polynomials is established, the continuity of rational functions (away from the points where the denominator is zero) is proven from QR. We also conclude that the graph of a rational function consists of several pieces -- one for each interval of its domain.
Example. For example, the function $$f(x)=\frac{1}{(x-1)^2(x-2)(x-3)}$$ has three holes, $1,2,3$, in its domain. Therefore, its graph has four branches. $\square$
The transcendental functions
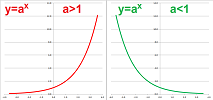
We consider the exponential function and justify treating this function as defined on $(-\infty,\infty)$.
Recall how in Chapter 1 we first defined the exponential function $f(x)=a^x,\ a>0$ for all integer values of $x$ as repeated multiplication. It was then also defined as repeated division in case of a negative $x$ in Chapter 4.
We then extended the definition to all rational numbers $x=\frac{p}{q}$ by means of the formula: $$a^{\frac{p}{q}}=\sqrt[q]{a^p}=\left( \sqrt[q]{a}\right)^p.$$
Now, what about $y=a^x$ for real values of $x$?
But first, the continuity.
We will assume the continuity of $y=e^x$ one single point, $x=0$.
Lemma. $$\lim_{x\to 0} e^x = 1.$$
Theorem. The exponential function $y=e^x$ -- defined for rational $x$ -- is continuous.
Proof. Consider: $$\begin{array}{lll} \lim_{h \to 0} e^{x_0 + h} &= \lim_{h \to 0} e^{x_0 } e^{h}&\text{ ...by Rule 1 of exponents...}\\ &= e^{x_0 } \cdot \lim_{h \to 0} e^{h} &\text{ ...by CMR...}\\ &= e^{x_0 } \cdot 1 &\text{ ...by the lemma...}\\ &= e^{x_0} . \end{array}$$ $\blacksquare$
Theorem. The natural exponential function, or the exponential function base $e$, also satisfies for each real $x$:
$$e^x=\lim_{n\to \infty}\left( 1+\frac{x}{n} \right)^n.$$
What about trigonometric functions? Let's review.
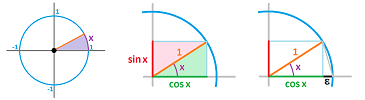
Suppose a real number $x$ is given. We construct a line segment of length $1$ on the plane. Then
- $\cos x$ is the horizontal coordinate of the end of the segment,
- $\sin x$ is the vertical coordinate of the end of the segment.
We think of $\cos x$ as the length of the shadow of the stick of length $1$ under angle $x$ in the ground when the sun is above it and $\sin x$ as the length of its shadow on the wall at sunset...
It is then plausible that -- as the stick rotates -- the length of the shadow changes continuously. Or the stick is still and it is the sun that is moving. Then the shadow gives us $\cos x$, where $x$ is a multiple of time:
We will assume the continuity of $\sin$ and $\cos$ at one single point, $x=0$.
Lemma. $$\lim_{x\to 0} \sin x = 0 \quad\text{ and }\quad \lim_{x\to 0} \cos x = 1.$$
Theorem. Both $\cos$ and $\sin$ are continuous at every $x$.
Proof. Consider: $$\begin{array}{lll} \lim_{h \to 0} \sin(a + h) &= \lim_{h \to 0} \left( \sin a \cdot \cos h + \cos a \cdot \sin h \right)&\text{ ...by a trig formula...}\\ &= \lim_{h \to 0} \left(\sin a \cdot \cos h\right) + \lim_{h \to 0} \left(\cos a \cdot \sin h\right) &\text{ ...by SR...}\\ &= \sin a \cdot \lim_{h \to 0} \cos h + \cos a \cdot \lim_{h \to 0} \sin h &\text{ ...by CMR...}\\ &= \sin a \cdot 1 + \cos a \cdot 0 &\text{ ...by the lemma...}\\ &= \sin a . \end{array}$$ $\blacksquare$
The theorem confirms that the graphs of $\sin$ and $\cos$ do indeed look like this, even if we zoom in on any point:
Below, we re-state the famous limits as facts about continuity.
Theorem (Famous limits). The following functions are continuous at every point: $$\begin{array}{ll} f(x)=\begin{cases} \frac{\sin x}{x} &\text{ if } x\ne 0;\\ 1& \text{ if } x=0; \end{cases}& g(x)=\begin{cases} \frac{1 - \cos x}{x} &\text{ if } x\ne 0;\\ 0 &\text{ if } x= 0. \end{cases} \end{array}$$
Limits and continuity under compositions
An application of PR in a simple situation reveals a new shortcut: $$\begin{array}{lll} \lim_{x\to a} \big( f(x) \big)^2 &=\lim_{x\to a} \left( f(x)\cdot f(x) \right)\\ &=\lim_{x\to a} f(x)\cdot \lim_{x\to a} f(x) \\ &=\left(\lim_{x\to a} f(x)\right)^2, \end{array}$$ provided that limit exists. Then, furthermore, a repeated use of PR produces a more general formula: $$\lim_{x\to a} f(x)^n = \left[ \lim_{x\to a} f(x) \right]^n,$$ for any natural number $n$. Thus, the limit of the power is equal to the power of the limit.
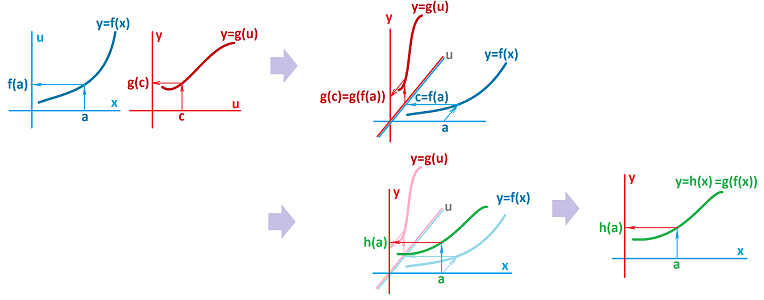
The conclusion is, in fact, about compositions of functions. Indeed, above we have: $$f(x)^n =g(f(x)) \text{ with } g(u)=u^n.$$ What is so special about this new function? It is continuous!
In brief, compositions of continuous functions are continuous. The idea is illustrated as follows. Imagine we have three curved wires with a freely moving nut on each. The nuts are connected by two rods. Then, if the first nut is moved, it moves the second, and the second moves the third:
We however first consider a limit at one given point.
Theorem (Composition Rule). If the limit at $a$ of function $f(x)$ exists and is equal to $L$ then so does that of its composition with any function $g$ continuous at $L$ and $$\lim_{x\to a} (g\circ f)(x) = g(L).$$
Proof. Suppose we have a sequence, $$x_n\to a.$$ Then, we also have another sequence, $$b_n=f(x_n).$$ The condition $f(x)\to L$ as $x\to a$ is restated as follows: $$b_n\to L \text{ as } n\to \infty.$$ Therefore, continuity of $g$ implies, $$g(b_n)\to g(L)\text{ as } n\to \infty.$$ In other words, $$(g\circ f)(x_n)=g(f(x_n))\to g(L)\text{ as } n\to \infty.$$ Since sequence $x_n\to a$ was chosen arbitrarily, this condition is restated as, $$(g\circ f)(x)\to g(L)\text{ as } x\to a.$$ $\blacksquare$
We can re-write the result as follows: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{|c|}\hline\quad \lim_{x\to a} (g\circ f)(x) = g(L)\Bigg|_{L=\lim_{x\to a} f(x)} \quad \\ \hline\end{array} $$ In a sense, the limit is, again, computed by substitution. Furthermore, the continuous $g$ can be moved out of the limit to be computed: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{|c|}\hline\quad \lim_{x\to a} g\bigg( f(x) \bigg) = g\left( \lim_{x\to a} f(x) \right) \quad \\ \hline\end{array} $$
Corollary. The composition $g\circ f$ of a function $f$ continuous at $x=a$ and a function $g$ continuous at $y=f(a)$ is continuous at $x=a$.
Proof. We apply the theorem and then the continuity of $f$: $$\lim_{x\to a}(g\circ f)(x)=g\left( \lim_{x\to a} f(x) \right)=g\left( f(a) \right)=(g\circ f)(a).$$ $\blacksquare$
The composition of continuous functions is illustrated below:
One can see now how the two continuous functions interact. First, we have their continuity described separately:
- 1. a small deviation of $x$ from $a$ produces a small deviation of $u=f(x)$ from $f(a)$, and
- 2. a small deviation of $u$ from $c$ produces a small deviation of $y=g(u)$ from $g(c)$.
If we set $c=f(a)$, we have:
- 3. a small deviation of $u=f(x)$ from $c=f(a)$ produces a small deviation of $y=g(u)=g(f(x))$ from $g(c)=g(f(a))$.
That's continuity of $h=g\circ f$ at $x=a$!
Example. From trigonometry, we know that $$\cos(x)=\sin(\pi/2-x).$$ The, the continuity of $\sin$ implies the continuity of $\cos$. $\square$
Example. Consider these two functions and their composition: $$\begin{array}{ll} y=g(u)&=u^2+2u-1,\\ u=f(x)&=2x^{-3}. \end{array}$$ What is the limit of $h=g\circ f$ at $1$?
First, we note that $g$ is continuous at every point as a polynomial. Therefore, by the theorem we have: $$\lim_{x\to 1} (g\circ f)(x) = g\left( \lim_{x\to 1} f(x) \right),$$ if the limit on the right exists. It does, because $f$ is a rational function defined at $x=1$: $$\lim_{x\to 1} f(x)=\lim_{x\to 1} 2x^{-3} =2\cdot 1^{-3}=2.$$ The limit becomes a number, $u=2$, and this number we substitute into $g$: $$\lim_{x\to 1} h(x) = g\left( \lim_{x\to 1} f(x) \right)=g(2)=2^2+2\cdot 2-1=7.$$
The answer is verified by a direct computation of $h$: $$h(x)=(g\circ f)(x) = g(f(x))=u^2+2u-1\Big|_{u=2x^{-3}}=\left( 2x^{-3} \right)^2+2\left( 2x^{-3} \right)-1=4x^{-6} +4x^{-3} -1.$$ Since the function is continuous (rational and defined at $1$), we have by substitution: $$\lim_{x\to 1} h(x)=4x^{-6} +4x^{-3} -1\Big|_{x=1}=4\cdot 1^{-6} +4\cdot 1^{-3} -1=7.$$ $\square$
We compute limits by verifying and then using, via CR, the continuity of the functions involved.
Example. Compute: $$\lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}.$$
We proceed by a gradual decomposition of $$r(x)= \frac{1}{\left( x^2+x-1 \right)^3}.$$ The last operation of $f$ is division. Therefore, $$r(x)=g(f(x)),\text{ where } u=f(x)=\left( x^2+x-1 \right)^3 \text{ and }g(u)=\frac{1}{u}.$$ Function $g$ is rational; but is it continuous? Its denominator isn't zero at the point we are interested in: $$f(0)=\left( x^2+x-1 \right)^3\Big|_{x=0}=\left( 0^2+0-1 \right)^3=-1\ne 0.$$ Then CR applies and our limit becomes: $$\lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}=\lim_{x\to 0} r(x)=\lim_{x\to 0} g(f(x))=g(\lim_{x\to 0}f(x))=\frac{1}{\lim_{x\to 0}\left[ \left( x^2+x-1 \right)^3\right]},$$ provided the new limit exits. Notice that the limit to be computed has been simplified!
Let's compute it. We start over and continue with a decomposition of $$p(x)= \left( x^2+x-1 \right)^3.$$ The last operation of $f$ is the power. Therefore, $$p(x)=g(f(x)),\text{ where } u=f(x)=x^2+x-1 \text{ and }g(u)=u^3.$$ Function $g$ is a polynomial and, therefore, continuous. Then CR applies and the limit becomes: $$\lim_{x\to 0} \left( x^2+x-1 \right)^3=\lim_{x\to 0} p(x)=\lim_{x\to 0} g(f(x))=g(\lim_{x\to 0}f(x))=\left[ \lim_{x\to 0}\left( x^2+x-1\right) \right]^3,$$ provided the new limit exits. Notice that, again, the limit to be computed has been simplified!
Let's compute it. We realize that the function $x^2+x-1$ is a polynomial and, therefore, its limit is computed by substitution: $$\lim_{x\to 0} \left( x^2+x-1\right) =x^2+x-1\Big|_{x=0}=0^2+0-1=-1.$$
What remains is to combine the three formulas above: $$\begin{array}{lll} \lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}&=\frac{1}{\left[\lim_{x\to 0}\left( x^2+x-1 \right)^3 \right]}\\ &=\frac{1}{\left[ \lim_{x\to 0}\left( x^2+x-1 \right) \right]^3}\\ &=\frac{1}{\left[ -1 \right]^3}\\ &=-1. \end{array}$$ $\square$
When there is no continuity to use, we may have to apply algebra (such as factoring), or trigonometry, etc. in order to find another decomposition of the function.
Our short list of continuous functions allows us to compute many limits; we just have to justify, every time, our conclusion by making a reference to this fact.
Example. First, $$\lim_{n\to \infty}\ln \left( 1+\frac{1}{n} \right) =\ln \left( \lim_{n\to \infty} \left[ 1+\frac{1}{n} \right]\right) =\ln 1=0,$$ because $\ln x$ is continuous at $x=1$. Second, $$\lim_{n\to \infty}\left( 1+\frac{1}{n} \right)^2 =\left( \lim_{n\to \infty} \left[ 1+\frac{1}{n} \right]\right)^2 =1^2=1,$$ because $x^2$ is continuous at $x=1$. Third, $$\lim_{n\to \infty}\frac{1}{1+\frac{1}{n}} =\frac{1}{ \lim_{n\to \infty}\left[ 1+\frac{1}{n} \right]} =\frac{1}{1}=1,$$ because $\tfrac{1}{x}$ is continuous at $x=1$. $\square$
Continuity of the inverse
So far, the only kind of function we know to be continuous is the rational functions: all algebraic operations, including compositions, on rational functions produce more rational functions. The continuity of even such a simple function as the square root $f(x)=\sqrt{x}$ remains unproven. But the inverse of this function is a polynomial!
Recall that functions are inverses when one undoes the effect of the other; for example,
- the multiplication by $3$ is undone by the division by $3$, and vice versa;
- the second power is undone by the square root (for $x\ge 0$), and vice versa;
- the exponential function is undone by the logarithm of the same base, and vice versa, etc.
Some of these functions are already known to be continuous. What about the rest?
The inverses undo each other under composition; two functions $y=f(x)$ and $x=g(y)$ are called inverse of each other when for all $x$ in the domain of $f$ and for all $y$ in the domain of $g$, we have: $$g(f(x))=x \text{ and } f(g(y))=y.$$ What if one of these functions, say $f$, is continuous? Does it make the other, $g$, continuous too? Considering the fact that the functions in the right-hand sides of these equations are also continuous, we expect the answer to be Yes.
Every function $y=f(x)$ which is one-to-one (i.e., there is only one $x$ for each $y$) has the inverse $x=g(y)$ which is also one-to-one (i.e., there is only one $y$ for each $x$). If we take the graph of the former and flip this piece of paper so that the $x$-axis and the $y$-axis are interchanged, we get the graph of the latter (and vice versa):
The shapes of the graphs are the same; in fact, it's the same graph! If one has no breaks then neither does the other. It is then conceivable that the continuity of one implies the continuity of the other. We just have to be careful about the location of the sequence. We know that $$x_n\to a\ \Longrightarrow\ f(x_n)\to f(a).$$ What about the converse?
Theorem. The inverse of a function $y=f(x)$ continuous at $x=a$, if exists, is a function $x=g(y)$ continuous at $b=f(a)$.
Proof. Suppose we have a sequence that converges to $b$: $$y_n\to b.$$ Since $f$ is onto, there is such $x_n$ for each $n$ that $f(x_n)=y_n$. Then we have: $$f(x_n)\to b= f(a).$$ .... $\blacksquare$
Thus, not only the rational functions are continuous (within their domains) but also their inverses. In particular, we have $$\lim_{x\to a} \sqrt{f(x)} = \sqrt{ \lim_{x\to a} f(x) }.$$ Since the odd powers are one-to-one but the even powers aren't one-to-one, we treat the odd and even roots separately.
The add roots have domains $(-\infty,\infty)$ while the even roots have domains $[0,\infty)$. The latter contains a special point, $0$, with the neighbors only on one side. That is why we need the concept of a one-sided limit in order to discuss continuity at such locations.
Definition. A function $y=f(x)$ is called continuous from the right at $x=a$ if $$\lim_{x\to a^+}f(x)=f(a);$$ and a function $y=f(x)$ is called continuous from the left at $x=a$ if $$\lim_{x\to a^-}f(x)=f(a);$$
Theorem. The odd roots, $y=\sqrt[3]{x},\ y=\sqrt[5]{x},\ y=\sqrt[7]{x},\ ...$ are continuous at every real $x$. The even roots, $y=\sqrt[2]{x},\ y=\sqrt[4]{x},\ y=\sqrt[6]{x},\ ...$ are continuous at every $x>0$ and continuous from the right at $x=0$.
Another important pair of inverses is the exponent and the logarithm. Since the former is continuous, then so is the latter.
As we know from Chapter 4, this function is increasing for all rational $x$. Then, from the Comparison Theorem, we conclude that it is also increasing on $(-\infty,\infty )$. Therefore, it is one-to-one.
Definition. The natural logarithm function, or the logarithm function base $e$, is defined as the inverse of the natural exponential function.
Definition. The exponential function base $a>0$ is defined by its values for each real $x$: $$a^x=e^{x\ln a}.$$
The definition matches the old one given for the rational $x$.
Theorem. The exponential function $y=a^x$ is continuous.
Proof. It follows from the continuity of $y=e^x$ and the Composition Rule for limits. $\blacksquare$
More on limits and continuity
To show continuity of functions beyond the rational functions, we will imply some indirect and direct methods.
Theorem (Comparison Test). Non-strict inequalities between functions are preserved under limits, i.e., if $$f(x) \leq g(x)$$ for all $n$ greater than some $N$, then $$\lim_{x\to a} f(x) \leq \lim_{x\to a} g(x), $$ provided the limits exist. Otherwise we have: $$\begin{array}{lll} \lim_{x\to a} f(x) =+\infty&\Longrightarrow& \lim_{x\to a} g(x)=+\infty;\\ \lim_{x\to a} f(x) =-\infty&\Longleftarrow& \lim_{x\to a} g(x)=-\infty. \end{array}$$
Exercise. Prove the theorem.
Warning: replacing the non-strict inequality, $$f(x) \leq g(x), $$ with a strict one, $$f(x) < g(x) ,$$ won't produce a strict inequality in the conclusion of the theorem.
From the inequality, we can't conclude anything about the existence of the limit:
Having two inequalities, on both sides, may work better.
It is called a squeeze, just as in the case of sequences. If we can squeeze the function under investigation between two familiar functions, we might be able to say something about its limit. Some further requirements will be necessary.
Theorem (Squeeze Theorem). If a function is squeezed between two functions with the same limit at a point, its limit also exists and is equal to the that number; i.e., if $$f(x) \leq h(x) \leq g(x) ,$$ for all $x$ within some open interval from $x=a$, and $$\lim_{x\to a} f(x) = \lim_{x\to a} g(x) = L,$$ then the following limit exists and equal to that number: $$\lim_{x\to a} h(x) = L.$$
Proof. For any sequence $x_n\to a$, we have: $$f(x_n) \leq h(x_n) \leq g(x_n).$$ We also have $$\lim_{n\to \infty} f(x_n) = \lim_{n\to \infty} g(x_n) = L.$$ Therefore, by the Squeeze Theorem for sequences we have $$\lim_{n\to \infty} h(x_n) = L.$$ $\blacksquare$
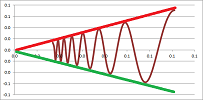
Example. Let's find the limit, $$\lim_{x \to 0}x \sin(\tfrac{1}{x}).$$
It cannot be computed by PR because $$\lim_{x\to 0}\sin(\tfrac{1}{x})$$ does not exist. Let's try a squeeze. This is what we know from trigonometry: $$-1 \le \sin(\tfrac{1}{x}) \le 1. $$ Note that this squeeze proves nothing about the limit of $\sin(\tfrac{1}{x})$:
Let's try another squeeze: $$-|x| \le x \sin(\tfrac{1}{x}) \le |x| .$$
Now, since $\lim_{x\to 0}(-x) =\lim_{x\to 0}(x)=0$, by the Squeeze Theorem, we have: $$\lim_{x\to 0} x \sin(\tfrac{1}{x})=0.$$ $\square$
Example. We can use the same logic to prove that the Dirichlet function multiplied by $x$ is continuous at exactly one point! $$xI_Q(x)=\begin{cases} x &\text{ if }x \text{ is a rational number},\\ 0 &\text{ if }x \text{ is an irrational number}. \end{cases}$$ Again, to plot its graph we can only draw two lines and then point out some of the missing points:
$\square$
Example. The first of the two famous limits: $$\lim_{x\to 0} \frac{\sin x}{x} =1, \ \lim_{x\to 0} \frac{1 - \cos x}{x} = 0.$$ follows by the Squeeze Theorem from this trigonometric fact: $$\cos x \le \frac{\sin x}{x} \le 1.$$ $\square$
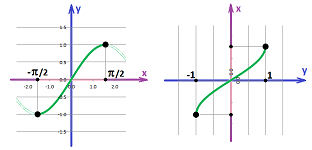
We would like to conclude that the inverses of $\sin$ and $\cos$ are also continuous. However, since neither function is one-to-one, we restrict the domain of the function to be able to define its inverse. First, we have a pair of inverse functions, the sine (restricted) and the arcsine: $$y=\sin x,\ x\in [-\pi/2,\pi/2], \text{ and } x=\sin^{-1}y,\ y\in [-1,1].$$
The graphs are of course the same with just $x$ and $y$ interchanged. Second, we have another pair of inverse functions, the cosine (restricted) and the arccosine: $$y=\cos x,\ x\in [0,\pi], \text{ and } x=\cos^{-1}y,\ y\in [-1,1].$$
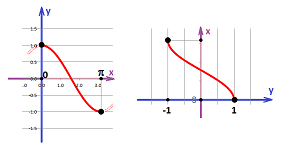
Thirdly, we also have this pair of inverse functions, the tangent (restricted) and the arctangent: $$y=\tan x,\ x\in (-\pi/2,\pi/2), \text{ and } x=\tan^{-1}y,\ y\in (-\infty,+\infty).$$
Since $$\tan x =\frac{\sin x}{\cos x},$$ we apply QR to conclude that it is continuous at every point $x$ with $\cos x\ne 0$. Let's consider one such point, $x=\pi/2$. We know that, as $x\to \pi/2$, we have $$\sin x\to 1 \text{ and } \cos x\to 0.$$ We should conclude that $$\tan x\to \pm\infty.$$ However, which infinity? We take into account the sign of $\cos x$ on the two sides of $\pi/2$: $$0<\cos x\to 0 \text{ as } x\to \pi/2^- \text{ and } 0>\cos x\to 0 \text{ as } x\to \pi/2^+.$$ Therefore, $$\tan x\to +\infty \text{ as } x\to \pi/2^- \text{ and } \tan x\to -\infty \text{ as } x\to \pi/2^+,$$ and, indeed, the graph reveals different behavior on the two sides of $\pi/2$. The pattern repeats itself every $\pi$ units on the $x$-axis.
We consider more examples of such behavior below.
Global properties of continuous functions
The definition of continuity is purely local: only the behavior of the function in the, no matter how small, vicinity of the point matters. Now, what if the function is continuous on a whole interval? What can we say about its global behavior?
Recall that a function $f$ is called bounded on an interval $[a,b]$ if its range is bounded, I.e., there is such a real number $Q$ that $$|f(x)| \le Q$$ for all $x$ in $[a,b]$.
Theorem. If the limit at $x=a$ of function $y=f(x)$ exists then $f$ is bounded on some interval that contains $a$: $$\lim_{x\to a}f(x) \text{ exists }\ \Longrightarrow\ |f(x)| \le Q$$ for all $x$ in $[a-\delta,a+\delta]$ for some $\delta >0$ and some $Q$.
Exercise. Prove the theorem.
We have been speaking until now of continuity only one point at a time: there is no cut at $x=a$.
Definition. A function $f$ is called continuous on interval $I$ if the interval is contained in the domain of $f$ and $$\lim_{n\to\infty}f(x_n)=f(x),$$ for any sequence $x_n$ in $I$ such that $x_n\to a$. Recall that it is simply called continuous when it is continuous on its domain.
Example. In particular, $1/x$ is continuous on $(-\infty,0)$ and on $(0,\infty )$. But it is not continuous on $(-\infty,\infty)$ or $(-\infty,0)\cup (0,\infty )$. $\square$
Proposition. (a) If $f$ is continuous on $[a,b)$ or $[a,b]$, then $f$ is continuous at every $x$ in $(a,b)$ and at $x=a$ from the right. (b) If $f$ is continuous on $(a,b]$ or $[a,b]$, then $f$ is continuous at every $x$ in $(a,b)$ and at $x=b$ from the left.
Example. In particular,
- $\sqrt{x}$ is continuous on $[0,\infty)$;
- $\sin^{-1}x$ and $\cos^{-1} x$ are continuous on $[-1,1]$.
$\square$
The global version of the above theorem guarantees that the function is bounded on any a closed bounded interval, i.e., $[a,b]$, as follows.
Theorem (Boundedness). A continuous on a closed bounded interval function is bounded on the interval.
Proof. Suppose, to the contrary, that $f$ is unbounded on interval $[a,b]$. Then there is a sequence $x_n$ in $[a,b]$ such that $f(x_n)\to \infty$. Then, by the Bolzano-Weierstrass Theorem, sequence $x_n$ has a convergent subsequence $y_k$: $$y_k \to y.$$ This point belongs to $[a,b]$! From the continuity, it follows that $$f(y_k) \to f(y).$$ This contradicts the fact that $y_k$ is a subsequence of a sequence that diverges to $\infty$. $\blacksquare$
In other words, the range of the function is within $[-Q,Q]$.
Exercise. Why are we justified to conclude in the proof that the limit $y$ of $y_k$ is in $[a,b]$?
Example. We show that the theorem fails if one of the conditions is omitted:
- (a) the function is discontinuous on a closed bounded interval;
- (b) the function is continuous on a not closed bounded interval;
- (c) the function is continuous on a closed unbounded interval.
In all three cases, the unbounded behavior of the function can be expressed as an infinite limit: $$\begin{array}{ll} \text{(a) }&\lim_{x\to c^-}f(x)=+\infty;\\ \text{(b) }&\lim_{x\to b^-}f(x)=+\infty;\\ \text{(a) }&\lim_{x\to +\infty}f(x)=+\infty;\\ \end{array}$$ However, we shouldn't equate unboundedness with infinite limits; here is the graph of $y=x\sin x$:
$\square$
Our understanding of continuity of functions has been as the property of having no gaps in their graphs. In fact, there are no gaps in the range either. To get from point $A=f(a)$ to point $B=f(b)$ we have to visit every point in between (no teleportation!):
We can see in the second part of the illustration how this property may fail.
This idea is more precisely expressed by the following.
Theorem (Intermediate Value Theorem). Suppose a function $f$ is defined and is continuous on interval $[a,b]$. Then for any $c$ between $f(a)$ and $f(b)$, there is $d$ in $[a,b]$ such that $f(d) = c$.
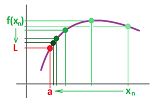
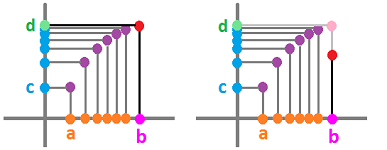
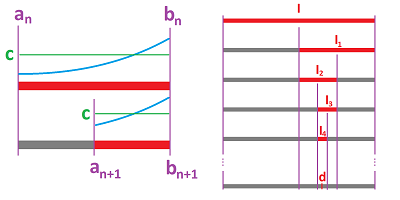
Proof. The idea of the proof is this: we will make the intervals in the $x$-axis that satisfy the condition of the theorem narrower and narrower; then the continuity of the function will ensure that the corresponding intervals in the $y$-axis will be getting narrower and narrower too.
More precisely, we will construct a sequence of nested intervals $$I=[a,b] \supset I_1=[a_1,b_1] \supset I_2=[a_2,b_2] \supset ...,$$ so that they have only one point in common. Consider the halves of $I=[a,b]$: $$\left[ a,\frac{a+b}{2} \right],\ \left[ \frac{a+b}{2},b \right].$$ For at least one of them, there is a change of $f$ from less to more or from more to less of $c$. Call this interval $I_1:=[a_1,b_1]$: $$f(a_1)<c,\ f(b_1)>c\quad \text{ or }\quad f(a_1)>c,\ f(b_1)<c.$$ Next, we consider the halves of this new interval: $$\left[ a_1,\frac{a_1+b_1}{2} \right],\ \left[ \frac{a_1+b_1}{2},b_1 \right].$$ Once again, for at least one of them, the values of $f$ cross $y=c$. Call this interval $I_2:=[a_2,b_2]$: $$f(a_2)<c,\ f(b_2)>c\quad \text{ or }\quad f(a_2)>c,\ f(b_2)<c.$$
Note that whenever $f(a_n)=c$ or $f(b_n)=c$, we are done.
We continue on with this process and the result is a sequence of intervals $$I=[a,b] \supset I_1=[a_1,b_1] \supset I_2=[a_2,b_2] \supset ...,$$ that satisfies these two properties: $$a\le a_1 \le ... \le a_n \le ... \le b_n \le ... \le b_1 \le b,$$ $$f(a_n)<c,\ f(b_n)>c\quad \text{ or }\quad f(a_n)>c,\ f(b_n)<c.$$ Also we have: $$|b_{n+1}-a_{n+1}|=\frac{1}{2} |b_n-a_n| = \frac{1}{2^n} |b-a| \to 0.$$
By the Nested Intervals Theorem, the sequences converge to the same values: $$a_n\to d,\ b_n\to d.$$ From the continuity of $f$, we then have: $$f(a_n)\to f(d),\ f(b_n)\to f(d).$$ By the Comparison Theorem, we conclude from the second property above: $$f(d)\le c,\ f(d)\ge c\quad \text{ or }\quad f(d)\ge c,\ f(d)\le c.$$ Hence, we have $$f(d)=c,$$ so $d$ is the desired number. $\blacksquare$
Choosing $c=0$ in the theorem gives us the following.
Corollary. If a continuous on interval function $f$ has the opposite signs at the end-points of $[a,b]$: $$f(a)>0,\ f(b)<0\quad \text{ or }\quad f(a)<0,\ f(b)>0,$$ then $f$ has an $x$-intercept between $a$ and $b$.
Exercise. Show that any odd degree polynomial has an $x$-intercept.
The proof of the Intermediate Value Theorem via the Nested Intervals Theorem is nothing more than an iterated search for a solution of the equation $f(x)=c$.
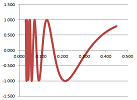
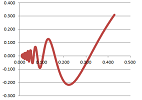
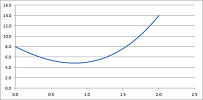
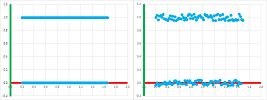
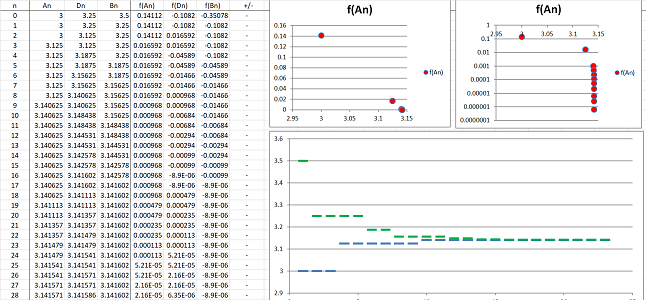
Example. Let's use the method to solve the equation: $$\sin x=0.$$ We start with the interval $[a_1,b_1]=[3,3.5]$. The function $f(x)=\sin x$ does change its sign over this interval. We divide the interval in half and pick the half over which $f$ also changes its sign. Then we repeat this process several times. The spreadsheet function for $a_n$ is: $$\texttt{=IF(R[-1]C[3]*R[-1]C[4]<0,R[-1]C,R[-1]C[1])},$$ and $b_n$: $$\texttt{=IF(R[-1]C[1]*R[-1]C[2]<0,R[-1]C[-1],R[-1]C)},$$ white $d_n$ is the mid-point of the interval.
We can see that the values of $a_n,\ b_n$ converge to $\pi$ and the values of $f(a_n),\ f(b_n)$ to $0$. The scatter plot of $(a_n,f(a_n))$ is shown on the right along with its version for a logarithmically re-scaled $y$-axis. $\square$
The theorem says that there are no missing values in the image of an interval.
Corollary. If the domain of a continuous function is an interval then so is its range.
Proof. It follows from the Intermediate Point Theorem. $\blacksquare$
This is how discontinuity may cause the range to have gaps:
The last graph shows that the converse of the theorem isn't true.
Recall from Chapter 4 that all strictly monotonic functions are one-to-one because the graph can't come back and cross a horizontal line for the second time:
The converse is true but only for continuous functions:
Corollary. Suppose $f$ is a continuous function on an interval $I$. Then, the function is one-to-one if and only if it is strictly monotonic.
Exercise. Prove the corollary.
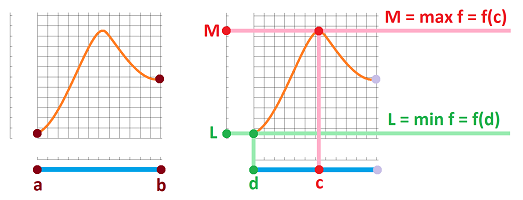
The image of an interval is an interval but is the image of a closed interval closed? If it is, the function reaches its extreme values, i.e., the least upper bound $\sup$ and the greatest lower bound $\inf$.
We repeat the definition from Chapter 4.
Definition. Given a function $y=f(x)$. Then $x=d$ is called a global maximum point of $f$ on interval $[a,b]$ if $$f(d)\ge f(x) \text{ for all } a\le x \le b;$$ and $x=c$ is called a global minimum point of $f$ on interval $[a,b]$ if $$f(c)\le f(x) \text{ for all } a\le x \le b.$$ (They are also called absolute maximum and minimum points.) Collectively they are all called global extreme points.
Just because something is described doesn't mean that it can be found. For example, $f(x)=1/x$ has no minimum value on $[0,\infty)$.
Theorem (Extreme Value Theorem). A continuous function on a bounded closed interval has a global maximum and a global minimum, i.e., if $f$ is continuous on $[a,b]$, then there are $c,d$ in $[a,b]$ such that $$f(c)\le f(x) \le f(d),$$ for all $x$ in $[a,b]$.
Proof. It follows from the Bolzano-Weierstrass Theorem. $\blacksquare$
Definition. Given a function $y=f(x)$. Then $x=M$ is called the global maximum value of $f$ on interval $[a,b]$ if it is the maximum element of the range of $f$; i.e., $$M\ge f(x) \text{ for all } a\le x \le b;$$ and $y=m$ is called the global minimum value of $f$ on interval $[a,b]$ if it is the minimum element of the range of $f$; i.e., $$m\le f(x) \text{ for all } a\le x \le b.$$ (They are also called absolute maximum and minimum value.) Collectively they are all called global extreme value. Such value of $x$ is called a global maximum point or global minimum point respectively.
Then the global max (or min) value is reached by the function at any of its global max (or min) points. For example, $f(x)=\sin x$ attains its max value of $1$ for infinitely many choices of $x=\pi /2,5\pi /2,...$.
Why are the restriction of the theorem essential?
Example. The function $1/x$ doesn't attain its least upper bound value on $(0,1]$ as it is, in fact, infinite.
The theorem doesn't apply because the interval isn't closed. Secondly, the function $1/x$ doesn't attain its greatest lower bound value, which is $0$, on $[1,\infty)$. The theorem doesn't apply because the interval isn't bounded.
Here $\sup$ isn't attained even though the interval is closed and bounded. The theorem doesn't apply because $f$ is not continuous. $\square$
Note that the reason we need the Extreme Value Theorem is to ensure that the optimization problem we are facing has a solution.
Example (Laffer curve). A typical continuity argument (outside mathematics) is as follows. The exact dependence of the revenue on the income tax rate is unknown. It is, however, natural to assume that both $0\%$ and $100\%$ rates will produce zero revenue.
If we also assume that the dependence is continuous, we conclude that increasing the rate may yield a decreasing revenue. $\square$
Exercise. What other implicit assumption are made in the example? Put the example in the form of a theorem and prove it.
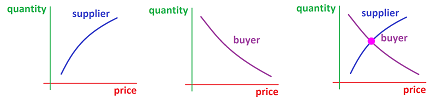
Example (supply and demand). Another continuity argument in economics is as follows. In a typical transaction, the supplier is willing to produce more of the commodity for a higher price. The buyer is prepared to buy more for a lower price. Then the quantity of the commodity is represented by two functions of price. The former is increasing and the latter is decreasing:
If we assume also that the two functions are continuous, we conclude that there must be a price that satisfies both parties. $\square$
Exercise. What other implicit assumption are made in the example? Put the example in the form of a theorem and prove it.
Large-scale behavior and asymptotes
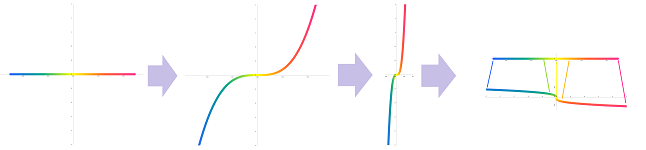
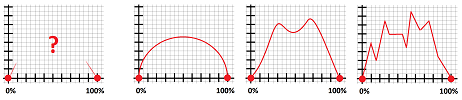
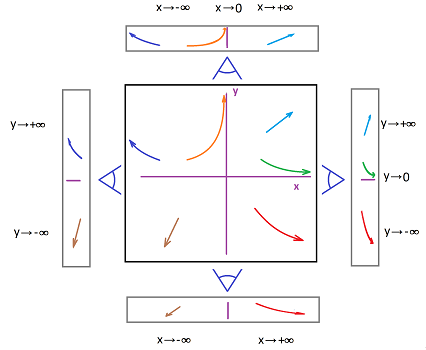
Graphs of most functions are infinite and won't fit into any piece of paper. They have to leave the paper and they do that in a number of different ways:
We just have to look at the $x$- and $y$-coordinates separately to determine the trend of the point $(x,y)$ in the plane. How? We can imagine walking on the curve and looking down on the $x$-axis to record the $x$-coordinates and looking forward or back to see what is happening the $y$-coordinate.
Alternatively, we imagine that the curves drawn on a piece of paper. Then, if we look at it at a sharp angle from the direction of the $x$-axis the change of $x$ becomes almost negligible and we clearly see the behavior of the $y$-coordinate. If we look from the direction of the $y$-axis, only the change of $x$ is significant.
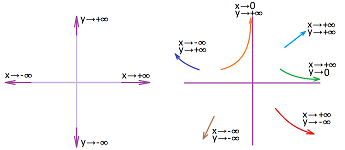
Conversely, what is we have the limit description of the curve, what does it look like? For example, we have:
- if $x\to +\infty$ and $y\to 0^+$, then we have: $(x,y) \searrow$;
- if $x\to 3^+$ and $y\to -\infty$, then we have: $(x,y) \swarrow$; etc.
If the point however approaches the line it can't cross ($y=0$ and $x=3$ in the above examples), the curve starts to become more and more straight and almost(!) merge with that line. The line is then called an asymptote.
Example. The simplest case, however, is the one with no asymptotes: $y=x,\ y=x^2, ...$ at $\pm\infty$, $y=e^x,\ y=\ln x$ at $+\infty$, and many more. $\square$
Definition. Given a function $f$, we say that $f$ goes to infinity if $$f(x_n)\to \pm\infty,$$ for any sequence $x_n\to \pm\infty$ as $n\to \infty$. Then we use the notation: $$f(x) \to \pm\infty \text{ as }x\to \pm\infty,$$ or $$\lim_{x\to\pm\infty}f(x)=\pm\infty.$$
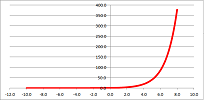
Example. We previously demonstrated the following: $$\lim_{x \to -\infty} e^{x} = 0, \quad \lim_{x \to +\infty} e^{x} = +\infty.$$
$\square$
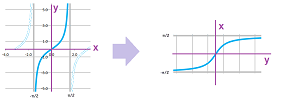
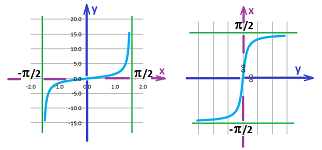
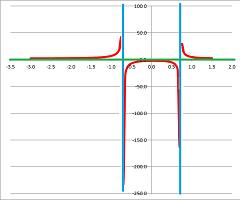
Example. As an illustration of the asymptotic behavior, we will consider the tangent $y=\tan x$ (restricted) and its inverse, arctangent: $$y=\tan x \text{ and } x=\tan^{-1}y,$$ for $-\pi/2 <x < \pi/2$.
The graphs are of course the same with just $x$ and $y$ interchanged.
Let's describe their large-scale behavior with limits. First the tangent: $$\tan x\to-\infty \text{ as } x\to -\pi/2^+ \text{ and } \tan x\to+\infty \text{ as } x\to \pi/2^-.$$ In other words, $$x\to -\pi/2^+,\ y\to-\infty \text{ and } x\to \pi/2^-,\ y\to+\infty.$$ Changing $x$ to be the dependent and $y$ to be the independent variables, we simply re-write the above for the arctangent: $$\tan^{-1} y\to-\pi/2^+ \text{ as } y\to -\infty \text{ and } \tan^{-1} y\to\pi/2^- \text{ as } y\to +\infty.$$ $\square$
Definition. Given a function $y=f(x)$, a line $y=p$ for some real $a$ is called a horizontal asymptote of $f$ if $$\lim_{n\to \infty}f(x_n)=p,$$ for any sequence $x_n\to -\infty$ or for any sequence $x_n\to +\infty$, as $n\to \infty$. Then we use the notation, respectively: $$\lim_{x\to -\infty}f(x)=p \text{ or } \lim_{x\to +\infty}f(x)=p.$$
Definition. A line $x=a$ for some real $a$ is called a vertical asymptote of $f$ if $$\lim_{n\to \infty}f(x)=\pm\infty,$$ for any sequence $x_n\to a^-$ or $x_n\to a^+$ as $n\to \infty$. Then we use the notation, respectively: $$\lim_{x\to a^-}f(x)=\pm\infty \text{ or } \lim_{x\to a^+}f(x)=\pm\infty.$$
Even though the two definitions look very different, they describe the identical behavior of the curve.
We can see the symmetry in the graph of $y=1/x$ and we can see it in the algebra: $$\begin{array}{lll} &x&y\\ \hline \text{horizontal: }& x\to +\infty & y\to 0\\ \text{vertical: }& x\to 0 & y\to +\infty \end{array}$$ We just interchange $x$ and $y$.
This operation is familiar.
Theorem. The vertical asymptotes of a function are the horizontal asymptotes of its inverse and vice versa.
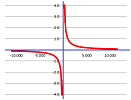
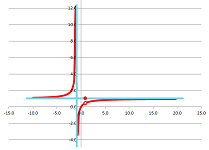
Example. Some functions have both kinds: $y=0$ is the horizontal asymptote (at both ends) and $x=0$ is the vertical asymptote of $y=1/x$. After all, this function is the inverse of itself! In more detail: $$\frac{1}{x}\to 0^- \text{ as }x\to -\infty,\ \frac{1}{x}\to 0^+ \text{ as }x\to +\infty, \frac{1}{x}\to -\infty \text{ as }x\to 0^-,\ \frac{1}{x}\to +\infty \text{ as }x\to 0^+.$$ $\square$
Example (Newton's Law of Gravity). The force of gravity between two objects is
- inversely proportional to the square of the distance between their centers.
In other words, the force is given by the formula: $$F = \frac{C}{r^2},$$ where:
- $C$ is some constant;
- $r$ is the distance between the centers of the mass of the two.
Then, if $r>0$ is variable, we have: $$ \lim_{r \to +\infty} F (r)= 0.$$ This means that the force becomes negligible when the two objects become sufficiently far away from each other. $\square$
Example (Newton's Law of Cooling). The law states that the difference between an object's temperature and the temperature of the atmosphere is declining exponentially. In other words, we have: $$T - T_{0} = Ce^{kx}, \ k<0,\ C>0,$$ where $T$ is the temperature and $T_{0}$ is the ambient temperature. We compute: $$\lim_{t\to +\infty}T(t)=T_0.$$ Therefore there is a horizontal asymptote $y = T_{0}$. The asymptote may be approached by the graph from above or from below:
- a warmer object cooling: $T - T_{0} > 0$ and $T \searrow$;
- a cooler object warming: $T - T_{0} < 0$ and $T \nearrow$.
$\square$
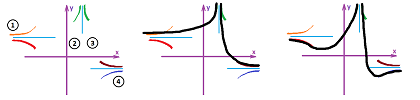
Example. Suppose we are facing the opposite (inverse!) problem: suppose we know the limits, now we need to plot the asymptotes and a possible graph of the function.
Suppose this is what we know about $f$: it is defined for all $x\ne 3$, and $$\lim_{x\to 3}f(x)=+\infty,\ \lim_{x\to -\infty}f(x)=3,\ \lim_{x\to +\infty}f(x)=-2.$$ Let's rewrite those:
- 1. $x\to -\infty,\ y\to 3$;
- 2. $x\to 3^-,\ y\to +\infty$;
- 3. $x\to 3^+,\ y\to +\infty$;
- 4. $x\to +\infty,\ y\to -2$.
We draw rough strokes to represent these facts, left:
The ambiguity about how the graph approaches the asymptotes remains at $-\infty$ and $+\infty$. We connect the initial strokes into a single graph (with two branches). Two possible versions of the graph of $f$ are shown on the right. $\square$
Example. The asymptote may be approached by the graph is the three main ways: $$\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right) = 1, \quad \lim_{x \to +\infty} \left( 2 - \frac{1}{x} \right) = 2, \quad \lim_{x \to +\infty} \left( \frac{1}{x}\cos x \right) = 0.$$
$\square$
Exercise. Use limits to describe the large-scale behavior of the function shown below:
Limits and infinity
Let's summarize the possible outcomes of our computations of limits: $$ \lim = \begin{cases} L & \rightarrow \text{ It's a number. You can do algebra with the limit.} \\ \pm\infty & \rightarrow \text{ You can do some algebra: } \infty + \infty = \infty \text{, but not other: } \infty - \infty = ?\\ \text{DNE} & \rightarrow \text{ Do no algebra with the limit.}\\ 0/0,\ \infty /\infty,\ \infty - \infty & \rightarrow \text{ It's indeterminate. Start over! } \end{cases}$$
Example. Let's fully investigate this function: $$f(x) = \begin{cases} \frac{x^{2} - x}{x^{2} - 1} & \text{ if } x \neq 1; \\ 1 & \text{ if } x = 1. \end{cases}$$ The point where the two formulas might conflict is $x=1$. The function is defined, but does the limit exist? Let's compute: $$\lim_{x\to 1} f(x) = \lim_{x \to 1} \frac{x^{2} - x}{x^{2} - 1}.$$ Plug in $x=1$. $$\frac{1^{1} - 1}{1^{2} - 1} = \frac{0}{0}. \quad \begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}$$ Indeterminate! We conclude that we need to do algebra with the function before turning back to the limit. $$\begin{aligned} \lim_{x \to 1} \frac{x^{2} - x}{x^{2} - 1} & = \lim_{x \to 1} \frac{x(x-1)}{(x-1)(x+1)} \\ & = \lim_{x \to 1} \frac{x}{x+1} \\ &= \frac{1}{1 + 1} = \frac{1}{2}. \end{aligned}$$ The last step is justified by the fact that the function $\frac{x}{x+1}$ is rational and, therefore, continuous at any point of its domain. Now, are the two one-sided limits equal? No: $1 \neq \frac{1}{2}$. That's why the function has a discontinuity at this point (a removable kind).
We can simplify the formula: $$f(x) = \begin{cases} \frac{x}{x+1} & \text{ if } x \neq 1, \\ 1 & \text{ if } x = 1. \end{cases}$$
We find the domain by solving: $x + 1 \neq 0$ and $x \neq 1$. The domain is $(-\infty,-1) \cup(-1,\infty).$
Consider $\frac{x}{x+1}$ at $x=-1$: $$\lim_{x \to -1}\frac{x}{x+1}=\infty.$$ Thus, $x=-1$ is a vertical asymptote.
However, there are still four different ways of how the graph can approach the asymptote. To tell which one, compute the one-sided limits while watching the signs of the numerator and the denominator: $$\begin{aligned} \lim_{x \to -1^{-}} \frac{x}{x+1} \left( = \frac{-}{-} = + \right) & = +\infty ,\\ \lim_{x \to -1^{+}} \frac{x}{x+1} \left( = \frac{-}{+} = - \right) & = -\infty. \end{aligned}$$
Next, the function's behavior at $\infty$: $$\lim_{x \to \infty} f(x) = \lim_{x \to \infty} \frac{x}{x+1} = 1. $$ Thus, $y=1$ is a horizontal asymptote.
Finally, we plot a rough sketch of the graph:
$\square$
Just as before, each property of limits is matched by its analog for limits at infinity.
Theorem (Algebra of Limits of Functions at Infinity). Suppose $f(x)\to F$ and $g(x)\to G$ as $x\to \pm \infty$. Then $$\begin{array}{|ll|ll|} \hline \text{SR: }& f(x)+g(x)\to F+G & \text{CMR: }& c\cdot f(x)\to cF& \text{ for any real }c\\ \text{PR: }& f(x)\cdot g(x)\to FG& \text{QR: }& f(x)/g(x)\to F/G &\text{ provided }G\ne 0\\ \hline \end{array}$$
Theorem (Substitution Rule). $$\lim_{x \to \infty} f(g(x)) = f\left( \lim_{x \to \infty} g(x) \right) $$ if $f$ is continuous at $L = \lim_{x \to \infty} g(x)$.
Example. Compute: $$\begin{array}{lrl} \lim_{x \to -\infty} \left( e^{x} - \frac{1}{x} + 3 \right) &\overset{\text{SR}}{=\! =\! =\! =} & \lim_{x \to -\infty} e^{x} - \lim_{x \to -\infty} \frac{1}{x} + \lim_{x \to -\infty} 3 \\ & = &0 - 0 + 3 \\ & = &3. \end{array}$$ $\square$
Example. Compute: $$\lim_{x \to \infty} \frac{x}{x + 1}. $$ Plugging in $x = \infty$, gives us $$\frac{\infty}{\infty} \quad \begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}$$ Facing an indeterminate expression, we are supposed to do algebra instead. What are we trying to accomplish? We want to get rid of the infinities in the numerator and the denominator. How about we divide both by $x$? $$\begin{array}{lrl} \lim_{x \to \infty} \frac{x}{x + 1} & = &\lim_{x \to \infty} \frac{\frac{x}{x}}{\frac{(x+1)}{x}} \\ &= &\lim_{x \to \infty} \frac{1}{1 + \frac{1}{x}} \\ &\overset{\text{QR}}{=\! =\! =\! =}& \frac{\lim_{x \to \infty} 1}{\lim_{x \to \infty} \left(1 + \frac{1}{x}\right)} \\ &\overset{\text{SR}}{=\! =\! =\! =}& \frac{1}{1 + 0} = 1. \end{array}$$ It worked! $\square$
Example. Evaluate the limit of this function at $\infty$: $$\frac{x^{2}}{x^{2} + 1}$$ Substitution leads to $$\frac{\infty}{\infty}, \quad \begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}$$ which is indeterminate. Let's divide by $x$ as last time. $$\begin{aligned} \frac{x^{2}}{x^{2} + 1} & = \frac{\frac{x^{2}}{x}}{\frac{(x^{2} + 1)}{x}} \\ & = \frac{x}{x + \frac{1}{x}} \to \frac{\infty}{\infty}. \end{aligned}$$ It's still indeterminate! We haven't eliminated the infinities. Let's divide by $x$ again, $$\begin{aligned} \frac{x}{x + \frac{1}{x}} & = \frac{\frac{x}{x}}{\frac{(x + \frac{1}{x})}{x}} \\ &= \frac{1}{1 + \frac{1}{x^{2}}} \\ &\to \frac{1}{1 + 0} \\ &= 1. \end{aligned}$$ Better idea: Divide by $x^{2}$ in the first place. $\square$
How do we evaluate the limit at $\infty$? For a rational function, the leading terms of the two polynomials determine the long term behavior of the numerator and denominator and, therefore, of the whole fraction.
Example. Consider: $$\lim_{x \to \infty} \frac{\overbrace{3x^{3}}^{\text{long-term}} - \overbrace{2x^{2} + x - 8}^{\text{short-term}}}{\underbrace{2x^{2}}_{\text{parabola}} - \underbrace{17x + 5}_{\text{where it is.}}} \to \frac{\infty}{\infty}. $$ This is what determines the long term: $$\frac{3x^{2}}{2x^{2}} = \frac{3}{2}x \to \infty.$$ To make this visible, we divide numerator and denominator by $x^{2}$. $$\begin{aligned} \lim_{x \to \infty} \frac{\frac{(3x^{3} - 2x^{2} + x - 8)}{x^{2}}}{\frac{(2x^{2} - 17x + 5)}{x^{2}}} & = \lim_{x \to \infty} \frac{3x - 2 + \frac{1}{x} - \frac{8}{x^{2}}}{2 - \frac{17}{x} + \frac{5}{x^{2}}} \\ & = \frac{\infty - 2 + 0 - 0}{2 - 0 + 0} \\ & = \infty. \end{aligned}$$ $\square$
- The lesson: To get rid of the indeterminacy, get rid of one of the infinities.
- The plan: Divide both parts of the fraction by $x$ to the degree of the denominator.
Example. Given $$ f(x) = \frac{x^{3} - x}{x^{2} - 6x + 5}. $$ At $\infty$, we have: $$\begin{aligned} \lim_{x \to \infty} \frac{x^{3} - x}{x^{2} - 6x + 5} &= \lim_{x \to \infty} \frac{\frac{x^{3} - x}{x^{2}}}{\frac{x^{2} - 6x + 5}{x^{2}}} \\ & = \lim_{x \to \infty} \frac{x - \frac{1}{x}}{1 - \frac{6}{x} + \frac{5}{x^{2}}} \\ & = \frac{\infty - 0}{1 - 0 - 0} \\ & = \infty. \end{aligned}$$ It's infinite, yes, but which infinity? We need to find the sign. We just find the signs of the leading terms of the numerator and denominator. $$\begin{array}{lll} \lim_{x \to +\infty} (x^{3} - x) = +\infty, & \lim_{x \to -\infty} (x^{3} - x) =-\infty;\\ \lim_{x \to +\infty} (x^{2} - 6x + 5) = +\infty, & \lim_{x \to -\infty} (x^{2} - 6x + 5) = +\infty. \end{array}$$ Conclusion: no horizontal asymptotes.
Now vertical asymptotes. We look at $$\frac{x^{3} - x}{x^{2} - 6x + 5}$$ and search for $0$ of the denominator. Let's factor both: $$\begin{gathered} x^{3} - x = x(x^{2} - 1) = x(x - 1)(x + 1)\\ x^{2} - 6x + 5 = (x-1)(x-5) \end{gathered}$$ We use the quadratic formula: $$\begin{aligned} x & = \frac{6 \pm \sqrt{6^{2} - 4\cdot 5}}{2} = \frac{6 \pm \sqrt{36 \cdot 20}}{2} \\ & = \frac{6 \pm 4}{2} = 5,1. \end{aligned}$$ Now, we have: $$f(x) = \frac{x(x-1)(x+1)}{(x-5)(x-1)} = \frac{x(x+1)}{x-5}$$ for $x \neq 1$ (that's the domain); $$\lim_{x \to 1} f(x) = \frac{1(1+1)}{1-5} = -\frac{1}{2},$$ because $\frac{x(x+1)}{x-5}$ is continuous at $1$. So $x=1$ is not a vertical asymptote. $$\lim_{x \to 5^{-}} \frac{x(x+1)}{x-5} = \frac{30}{0} = \overset{?}{\pm} \infty$$ Therefore, $x=5$ is a vertical asymptote. But which infinity? We need to find the sign. $$\frac{ + \cdot +}{-} = \; -$$ We conclude: $$\lim_{x \to 5^{-}} \frac{x(x+1)}{x-5} = - \infty.$$ Similarly, we find: $$\lim_{x \to 5^{+}} f(x) = +\infty.$$ $\square$
Some facts about limits of sequences can be restated for functions.
First, recall the lesson about the behavior of polynomials at $\infty$:
- only the leading term matters.
Theorem (Limits of polynomials). Suppose we have a polynomial of degree $p$ with the leading coefficient $a_p\ne 0$. Then its limit is: $$\lim_{x\to \pm\infty}(a_px^p+a_{p-1}x^{p-1}+...+ a_1x+a_0)=\begin{cases} \pm\infty &\text{ if } a_p>0;\\ \mp\infty &\text{ if } a_p<0. \end{cases}$$
Then, if we zoom out on the graph of a polynomial, we will see just four possible patterns
A more general result is about rational functions.
Theorem (Limits of rational functions). Suppose we have a rational function represented as a quotient of two polynomials of degrees $p$ and $q$, with the leading coefficients $a_p\ne 0,\ b_q\ne 0$. Then the limit of this function is: $$\lim_{x\to +\infty}\frac{a_px^p+a_{p-1}x^{p-1}+...+ a_1x+a_0}{b_qx^q+b_{q-1}x^{q-1}+...+ b_1x+b_0}=\begin{cases} \infty&\text{ if } p>q;\\ \frac{a_p}{b_p}&\text{ if } p=q;\\ 0&\text{ if } p<q. \end{cases}$$
Exercise. State the above theorem for $x\to -\infty$.
The long-term behavior of a rational function is determined by the leading terms of its numerator and denominator: $$\lim_{x\to\infty}\frac{a_px^p+a_{p-1}x^{p-1}+...+ a_1x+a_0}{b_qx^q+b_{q-1}xx^{q-1}+...+ b_1x+b_0}=\lim_{x\to\infty}\frac{a_px^p}{b_px^q}=\frac{a_p}{b_p}\lim_{x\to\infty}x^{p-q}.$$ The picture is complicated -- in comparison to polynomials -- by that fact that rational functions also have horizontal and vertical asymptotes.
Example. Sometimes we face indeterminate expressions with functions other than rational. Evaluate: $$\lim_{x\to \infty} \left(\sqrt{x^{2} + 1} - x \right). $$ Substitution gives us: $$\infty - \infty, \quad \begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}$$ which is indeterminate. The trick is to multiply and divide by the “conjugate”: $$\sqrt{x^{2} + 1} + x.$$ This is the result: $$\begin{aligned} \lim_{x\to \infty} \frac{\left(\sqrt{x^{2} + 1} - x \right)\left(\sqrt{x^{2} + 1} + x\right)}{\sqrt{x^{2} + 1} + x} & = \lim_{x\to \infty} \frac{(x^{2} + 1) - x^{2}}{\sqrt{x^{2} + 1} + x} \\ & = \lim_{x \to \infty} \frac{1}{\sqrt{x^{2} + 1} + x} \\ & = \frac{1}{\infty} \\ & = 0. \end{aligned}$$ $\square$
Continuity and accuracy
The idea of continuity can be introduced and justified by considering the accuracy of a measurement.
Suppose we have a collection of square tiles of various sizes and we need to find the area $A$ of each of them in order to know how many we need to cover the whole floor.
The answer is, of course, to measure the side, $x$, of each tile and then compute: $$A=x^2.$$ For example, we have: $$x=10\Longrightarrow A=100.$$
But what if the measurement isn't fully accurate; for example, $$x=10 \pm .3.$$ As a result, the computed value of the area of the tile -- what we care about -- will also have some error! Indeed, the area won't be just $A=100$ but $$A=(10 \pm .3)^2 .$$ Therefore, $$\begin{array}{lll} A&=10^2 \pm 2 \cdot 10 \cdot .3 +.3^2 \\ &=100.09 \pm 6. \end{array}$$ The meaning of the result is that the actual area must be somewhere within the interval $(94.09,106.09)$.
Suppose next that we can always improve the accuracy of the measurement of the side of the tile $x$ -- as much as we like. The question is, can we also improve the accuracy of the computed value of $A$. Can we achieve this accuracy to anybody's satisfaction, even if this standard of accuracy might change?
Let's make it specific. Suppose $x=10$. The above computation shows that if the desired accuracy of $A$ is $\pm 5$, we haven't achieved it with the given accuracy of measurement $x$, which is of $\pm .3$. We can easily show, however, that $\pm .2$ would solve the problem: $$\begin{array}{lll} A&=(10 \pm .2)^2=10^2 \pm 2 \cdot 10 \cdot .2 +.2^2 \\ &=100.04 \pm 4. \end{array}$$ It follows that the actual area must be within $4.04$ from $100$.
Let's rephrase this problem in order to solve it for all possible values of the desired accuracy of $A$.
Let's assume that the measurement of the side is $a$ and, therefore, the assumed area $A$ is $a^2$. Now suppose we want the deviation of $A$ form the true area to be some small value $\varepsilon >0$ or better. What deviation $\delta$ of $a$ from $x$ do we need to be able to guarantee that?
Suppose the actual length is $x$ and, therefore, the actual area is $A=x^2$. Then we want to ensure that $A$ is within $\varepsilon$ from $a^2$ by making sure that $x$ is within $\delta$ from $a$. What should $\delta$ be?
To rephrase algebraically, we want to find $\delta$ such that $$|x-a| <\delta \Longrightarrow |x^2-a^2|<\varepsilon.$$
The definition suggested by the above discussion is as follows.
Definition. A real-valued function $f$ is called continuous at $x=a$ if for any $\epsilon >0$ there is $\delta >0$ such that $$|x-a| <\delta \Longrightarrow |f(x)-f(a)|<\varepsilon.$$
Thus the answer to our question is:
- yes, we can always improve the accuracy of the computed value of $A=x^2$ -- to anybody's satisfaction -- by improving the accuracy of the measurement of $x$.
Exercise. Prove that $f(x)=x^2$ is continuous at $x=0,\ x=1,\ x=a$.
Exercise. Carry out this kind of analysis for: a thermometer put in a cup of coffee to find its temperature. Assume that the thermometer gives perfect readings. Hint: it'll take time for it to warm up.
Exercise. What is the relation between $\varepsilon$ and $\delta$ when $f$ is linear?
To further illustrate the idea, let's consider a different situation. Suppose we don't care about the area anymore; we just want to fit these tiles into a strip $10$ inches wide. We take a tile and if it fits, it is used; otherwise, it is discarded.
Then, we still get a measurement $a$ of the side of the tile but our real interest is whether $a$ is less or more than $10$. Just as in the previous example, we don't know the actual length $x$ exactly; it's always within some limits: $5.0 \pm 0.5$ or $a \pm \delta$. Here $\delta$ is the accuracy of measurement of $x$. The algebra is much simpler than before. For example, if the length is measured as $11$, we need the accuracy $\delta=1$ or better to make the determination. It's the same for the length $9$.
But what if the measurement is exactly $10$? Even if we can improve the accuracy, i.e., $\delta$, as long as $\delta > 0$, we can't know whether $x$ is larger or smaller than $10$.
Let's define a function that makes this decision: $$f(x)=\begin{cases} 1 \quad\text{ (pass) } & \text{ if } x \le 10, \\ 0 \quad\text{ (fail) } & \text{ if } x > 10. \end{cases}$$ Suppose we need the accuracy of $y = f(x)$ to be $\varepsilon = 0.5$. Can we achieve this by decreasing $\delta$? In other words, can we find $\delta$ such that $$|x-10|<\delta \Longrightarrow |f(x)-1|<\varepsilon ?$$ Of course not: $$x>10 \Longrightarrow |f(x)-1|=|0-1|=1.$$
Thus, the answer to our question is:
- No, we cannot always improve the accuracy of the computed value of $f(x)$ -- to anybody's satisfaction -- by improving the accuracy of the measurement of $x$.
The reason to be quoted is that $f$ is discontinuous at $x=10$.
Exercise. Carry out this kind of analysis for: the total test score vs. the corresponding letter grade. What if we introduce A-, B+, etc.?
We next pursue this idea of continuity of the dependence of $y$ on $x$, stated as:
- we can ensure the desired accuracy of $y$ by increasing the accuracy of $x$.
We discuss limits first.
The $\varepsilon$-$\delta$ definition of limit
We can define limits and continuity of functions without invoking limits of sequences. Let's start over. We re-write what we want to say about the meaning of the limits in progressively more and more precise terms. $$\begin{array}{l|ll} x&y=f(x)\\ \hline \text{As } x\to a, & \text{we have } y\to L.\\ \text{As } x\text{ approaches } a, & y\text{ approaches } L. \\ \text{As } \text{the distance from }x \text{ to } a \text{ approaches } 0, & \text{the distance from }y \text{ to } L \text{ approaches } 0. \\ \text{As } |x-a|\to 0, & \text{we have } |y-L|\to 0.\\ \text{By making } |x-a| \text{ as smaller and smaller},& \text{we make } |y-L| \text{ as small as needed}.\\ \text{By making } |x-a| \text{ less than some } \delta>0 ,& \text{we make } |y-L| \text{ smaller than any given } \varepsilon>0. \end{array}$$
Definition. The limit of function $f$ at $x=a$ is a number $L$, if exists, such that for any $\varepsilon >0$ there is such a $\delta> 0$ that $$0<|x-a|<\delta \ \Longrightarrow\ |f(x)-L|<\varepsilon.$$
This is the geometric meaning of the definition: if $x$ is within $\delta$ from $a$, then $f(x)$ is supposed to be within $\varepsilon$ from $L$. In other words, this part of the graph fits within the $\varepsilon$-band around the line $y=L$.
This is the “$\varepsilon$-$\delta$ definition” of limit of a function. It matches the definition of limit of a sequence which can now be called the “$\varepsilon$-$N$ definition”.
Theorem. The two definitions of the limit of a function are equivalent.
Proof. $[\varepsilon$-$\delta \Rightarrow \varepsilon$-$N]$ Suppose $x_n\to a$. Suppose now that $\varepsilon>0$ is given. As the definition above is satisfied, there is a $\delta> 0$ that $$0<|x-a|<\delta \ \Longrightarrow\ |f(x)-L|<\varepsilon.$$ On the other hand, we have: $$|x_n-a|<\delta \text{ for all } n>N,$$ for some $N$. Therefore, for all $n>N$, we have $$|f(x_n)-L|<\varepsilon.$$ This means that $f(x_n)\to L$.
$[\varepsilon$-$N \Rightarrow\varepsilon$-$\delta]$ .... $\blacksquare$
As an exercise, let's compute the limit of an arbitrary linear function. The relation between $\delta$ and $\varepsilon$ is predicable:
Theorem. For a linear function $f(x)=mx+b$ with $m\ne 0$, the definition of limit is satisfied for $$\delta = \varepsilon / |m|.$$
Proof. $$\begin{array}{lll} |x-a|<\delta &\Longleftrightarrow\ |x-a|<\varepsilon / |m|\\ &\Longleftrightarrow\ |m| \cdot |x-a|<\varepsilon \\ &\Longleftrightarrow\ |m \cdot (x-a)|<\varepsilon \\ &\Longleftrightarrow\ |mx-ma|<\varepsilon \\ &\Longleftrightarrow\ |(mx+b)-(ma+b)|<\varepsilon \\ &\Longleftrightarrow\ |f(x)-f(a)|<\varepsilon . \end{array}$$ $\blacksquare$
Corollary. $$\lim_{x\to a} (mx+b)=ma+b.$$
Proof. We just need to consider the case $m=0$. The definition is trivially satisfied for $L=b$ and any $\delta$ and $\varepsilon>0$: $$0<|x-a|<\delta \ \Rightarrow\ |f(x)-L|=|b-b|=0<\varepsilon.$$ $\blacksquare$
Example. Prove the limit by using the definition: $$\lim_{x \to -1.5}\frac{9 - 4x^2}{3 + 2x} = 6 .$$
Plugging $x=-1.5$ gives us an indeterminate expression: $$\frac{9 - 4x^2}{3 + 2x}\Bigg|_{x = -1.5} \leadsto \frac{0}{0}\ \begin{array}{|c|}\hline \ \text{ DEAD END }\ \\ \hline\end{array}.$$
We start over. Let's match what we want to prove with the definition: $$\lim_{x \to \underbrace{-1.5}_{a}} \underbrace{\frac{9 - 4x^2}{3 + 2x}}_{f(x)} = \underbrace{6}_{L}.$$
We replace $f(x)$ with a simpler expression, equal for all $x \neq -1.5$: $$ \begin{aligned} \dfrac{9 - 4x^{2}}{3 + 2x} &= \dfrac{3^{2} - (2x)^{2}}{3 + 2x} \\ & = \dfrac{(3 + 2x)(3 - 2x)}{3 + 2x} \\ & = 3 -2x, \end{aligned} $$ for all $x$ for which $3 + 2x \neq 0$, or $x \neq 1.5$
Now, this expression is linear! Then the dependence of $\delta$ on $\varepsilon$ is simple, as we know: $$\delta = \frac{\varepsilon}{2}.$$ Then we need to demonstrate the following: $$ 0 < | x - (-1.5)| < \dfrac{\varepsilon}{2} \overset{?}{\Longrightarrow} |3 - 2x - 6| < \varepsilon$$ Then, we re-write it: $$ \begin{aligned} 0 < | x + 1.5| < \dfrac{\varepsilon}{2} \overset{?}{\Longrightarrow} & |-3 - 2x| < \varepsilon,\\ 0 < | x + 1.5| < \dfrac{\varepsilon}{2} \overset{?}{\Longrightarrow}& | 2x + 3| < \varepsilon,\\ 0 < | x + 1.5| < \dfrac{\varepsilon}{2} \overset{?}{\Longrightarrow}& | x+ 1.5 | < \dfrac{\varepsilon}{2}. \end{aligned} $$ It works! The definition is satisfied. $\square$
Things aren't as simple for non-linear functions.
Example. Let's consider first $f(x)=x^2$ at $a=0$. We expect the limit to be $L=0$. But what is the value of $\delta$ in terms of $\varepsilon$? $$\begin{array}{lll} |f(x)-L|<\varepsilon &\Longleftrightarrow\ |x^2|<\varepsilon\\ &\Longleftrightarrow\ |x|^2<\varepsilon\\ &\Longleftrightarrow\ |x|<\sqrt{\varepsilon} . \end{array}$$ Thus, we have discovered that $\delta=\sqrt{\varepsilon}$ works in the definition. $\square$
Example. However, this is how changing the location from $a=0$ to $a=1$ complicates things: $$\begin{array}{lll} |f(x)-L|<\varepsilon &\Longleftrightarrow\ |x^2-1|<\varepsilon\\ &\Longleftrightarrow\ |(x-1)(x+1)|<\varepsilon\\ &\Longleftrightarrow\ |x-1|<\frac{\varepsilon}{|x+1|}\\ &\Longleftarrow\ |x-1|<\delta<\frac{\varepsilon}{|x+1|} . \end{array}$$ To find such a $\delta$, we have to proceed to estimating of $|x+1|$, just as we did before. The reason for this complication is explained by the fact that the graph of $y=x^2$ curves differently on the left and on the right of $a=1$. $\square$
Example. Let's consider the sign function around $0$: $$f(x) = \operatorname{sign}(x) = \begin{cases} -1& \text{ if } x < 0, \\ 0 & \text{ if } x = 0, \\ 1 & \text{ if } x >0. \end{cases}$$
Our guess is that $\lim_{x \to 0} f(x)$ does not exist but, for now, we will just show that $L = 1$ is not the limit. We need to show that there is no $\delta$ satisfying this condition for some $\varepsilon > 0$. Pick $\varepsilon = 1$. Is there $\delta > 0$ such that: $$ 0 < |x - \overbrace{0}^{a}| < \delta \Rightarrow |\underbrace{\overbrace{\text{sign}(x)}^{f(x)} - \overbrace{1}^{L}| < \varepsilon = 1}_{f(x) \text{ is within } (0,2)}.$$ What $x$ would violate this?
Any $x < 0$ since we have then $f(x) = -1$. The definition fails, so $L = 1$ is not the limit. $\square$
Exercise. Prove that $L=0$ isn't the limit either.
In order to learn how to disprove the existence of limit, let's state the negation of the definition.
Theorem. A number $L$ is not the limit of function $f$ at $x=a$ if there is an $\varepsilon >0$ such that for any $\delta> 0$ and some $x$ we have $$0<|x-a|<\delta \text{ and } |f(x)-L| \ge \varepsilon.$$
Example. Let's prove the non-existence of limit at $a=0$ for the sign function $f(x)=\operatorname{sign}(x)$. Suppose $L\ne 0$ is any number. Let's pick $\varepsilon =|L|/2$. Now suppose $\delta>0$ is arbitrary and suppose for some $x\ne 0$ we have $$0<|x|<\delta \text{ and } |f(x)-L| < \varepsilon = |L|/2.$$ Then, $f(x)$ is of the same sign as $L$. But what does this say about $-x$? We also have: $$0<|-x|<\delta \text{ and, therefore, } |f(-x)-L| < \varepsilon = |L|/2.$$ Then, $f(-x)$ is also of the same sign as $L$. This contradicts the fact that $f(-x)=-f(x)$. $\square$
Let's prove the Composition Rule independently from this new definition. These are the three instances of the definition we face; we need to prove part 3 from parts 1 and 2:
- 1. $y=g(x)\to L$ as $x\to a$, i.e., any $\not\varepsilon\ \gamma>0$ there is such a $\delta> 0$ that
$$0<|x-a|<\delta \ \Longrightarrow\ |g(x)-L|<\not\varepsilon\ \gamma;$$
- 2. $z=f(y)\to M$ as $y\to L$, i.e., any $\varepsilon >0$ there is such a $\not\delta\ \gamma> 0$ that
$$0<|y-L|<\not\delta\ \gamma \ \Longrightarrow\ |f(y)-M|<\varepsilon;$$
- 3. $z=f(g(x))\to M$ as $x\to a$, i.e., any $\varepsilon >0$ there is such a $\delta> 0$ that
$$0<|x-a|<\delta \ \Longrightarrow\ |f(g(x))-M|<\varepsilon.$$ Above we reconcile the parameters, $\varepsilon$ and $\delta$, that appear in each, by matching the three variables: a small deviation of $x$ (how small: within $\delta$) causes a small deviation of $y$ (call it $\gamma$), which in turn causes a small deviation of $z$ (that's $\varepsilon$).
Suppose now $\varepsilon >0$ is given. Then the $\gamma$ found, from this $\varepsilon$, in part 2 is fed into part 1 producing a $\delta$. Combining these two statements together, we have: $$\begin{array}{lll} 0<|x-a|<\delta &\Longrightarrow\ |g(x)-L|<\gamma, &\quad \text{ let } y=g(x)\\ &\Longrightarrow\ |y-L|<\gamma &\Longrightarrow\ |f(y)-M|<\varepsilon \end{array}$$ Part 3 is proven!
Theorem (Composition). Suppose
- 1. $y=g(x)\to L$ as $x\to a$, and
- 2. $z=f(y)\to M$ as $y\to L$.
Then
- 3. $z=(f\circ g)(x)\to M$ as $x\to a$.
Exercise. Prove that if $f$ and $g$ are continuous at $x=a$, the so are $\max\{f,g\}$ and $\min\{f,g\}$.
We have required that if $x$ is within $\delta$ from $a$, then $f(x)$ is within $\varepsilon$ from $L$. We are referring here to intervals -- one containing $a$ and another $L$ -- but not just any; these intervals are centered at these points. This symmetry requirement isn't necessary.
Even when we start with a symmetric interval around $a$, the symmetry around $L$ only appears when the function is linear.
Theorem. The limit of a function $f$ at $x=a$ is $L$ if and only if for any $\varepsilon_1,\ \varepsilon_2 >0$ there are such $\delta_2, \ \delta_2 > 0$ that $$-\delta_1<x-a<\delta_2 \ \Longrightarrow\ -\varepsilon _1 <f(x)-L<\varepsilon _2.$$
The theorems supply an alternative definition of limit, and of continuity.
Exercise. (a) Prove the above theorem. (b) Use the above theorem to prove the Composition Theorem above. (c) Use the above theorem to prove that the inverse of a continuous function is continuous.