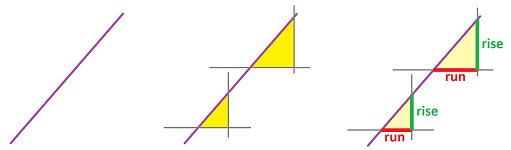
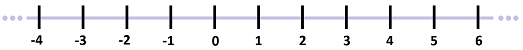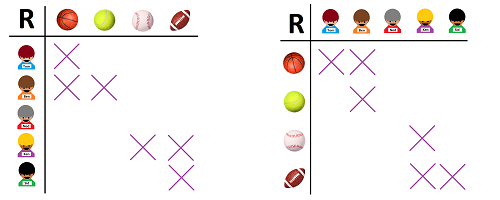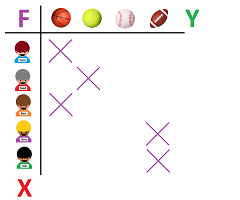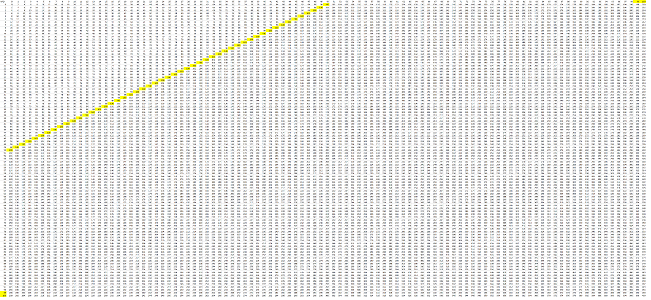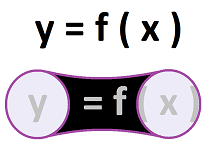This site is being phased out.
Functions
Contents
- 1 Sets and relations
- 2 Functions
- 3 Sequences are numerical functions
- 4 How numerical functions emerge: optimization
- 5 Set building
- 6 The $xy$-plane: where graphs live...
- 7 Linear relations
- 8 Relations vs. functions
- 9 A function as a black box
- 10 Give the function a domain...
- 11 The graph of a function
- 12 Linear functions
- 13 Algebra creates functions
- 14 The arithmetic operations on functions
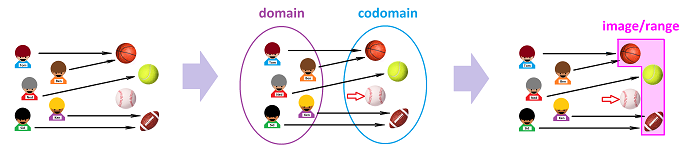
- 15 The image: the range of values of a function
Sets and relations
In mathematics, we refer to any loose collection of objects or entities -- of any nature -- as a set.
For example, is this a circle in a bag of marbles? No, the marbles it is made of aren't connected to each other or to any location.
One shake and the circle is gone!
Example (lists). Sets given explicitly -- as lists -- are simplest ones:
- a roster of students: Adams, Adkins, Arrows, ...;
- a list of numbers: 1,2,3,4, ...;
- a list of planets: Mercury, Venus, Earth, Mars, ...;
- and so on.
The order at which they appear on the list is not a part of the information we care about when we speak of sets. $\square$
Example (“sets”). The idea of set contrasts with such expressions as “a set of silverware” when the word “set” suggests a certain structure: specific types of knives and forks with a specific place in the box. It is the same set, mathematically, whether the items are arranged in a box or piled up on the counter. A set of encyclopedia consists of books that can be arranged alphabetically or chronologically or randomly. $\square$
What creates a set is our knowledge or ability to determine whether an object belongs or does not belong to it.
Example (conditions). A roster of a class produces a set of the students in this class. On the other hand, the female students in the class also form a set even if there is no such list; we can just go down the roster and determine if a student belongs to this new set. Similarly, the students with an A on the last test also -- implicitly -- form a set. $\square$
Example (math). A lot of sets examined early in this book will be sets of numbers. For example, take the set of even numbers; then we know that $2$ belongs to it but $3$ does not. Another example from mathematics is sets of points on the plane: straight lines, triangles, circles and other curves, etc.
We can tell whether a point belongs to the set... $\square$
Example (non-sets). If the condition is vague, we don't have a set: “interesting novels”, “bad paintings”, etc. When the condition is nonsensical, we don't have a set either: “fast trees”, “blue numbers”, etc. $\square$
Exercise. Give your own examples of (a) sets as lists, (b) sets defined via conditions, and (c) non-sets.
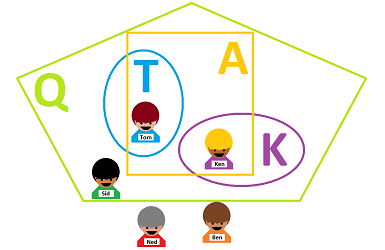
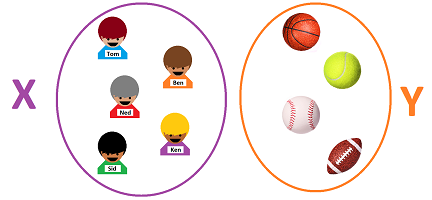
In the rest of this chapter we will use the following example. These five boys form a set:
On the one hand, they are individuals and cannot be interchanged within the set. On the other hand, they are unrelated to each other: we can list them in any order, we can arrange them in a circle, a square, or at random, we can change the distances between them, and so on. It's the same set! The members of a set are called its elements.
A set is then nothing but a list:
- Tom,
- Ken,
- Sid,
- Ned,
- Ben.
Or: “Tom, Ken, Sid, Ned, Ben”, in any order.
Warning: as there is no order, elements of a set aren't to be confused with terms of a sequence.
There is a specific mathematical notation for finite sets; we put the list in braces: $$\begin{array}{lll} &\{\text{ Tom }, \text{ Ken }, \text{ Sid }, \text{ Ned }, \text{ Ben }\}\\ =&\{\text{ Ned }, \text{ Ken }, \text{ Tom }, \text{ Ben }, \text{ Sid }\}\\ =&\{\text{ Ben }, \text{ Ken }, \text{ Sid }, \text{ Tom }, \text{ Ned }\}\\ =&\ ... \end{array}$$ All of these are equally valid representations of the set.
Exercise. How many such representations are there? Hint: in how many ways can you permute these five elements?
Definition. Two sets $X$ and $Y$ are equal if every element of $X$ is also an element of $Y$ and vice versa.
Repetitions aren't allowed! Or, at least, they are to be eliminated: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccc} \{\text{ Tom }, \text{ Ken }, \text{ Sid }, \text{ Ned }, \text{ Ben }, \text{ Ben }\}& \ra{ \text{ remove repetitions! } }&\{\text{ Tom }, \text{ Ken }, \text{ Sid }, \text{ Ned }, \text{ Ben }\}. \end{array}$$
Just as the boys have names, the set also needs one. We can call this set “Team”, or “Boys”, etc. To keep things compact, let's give it a short name, say $X$: $$X=\{\text{ Tom }, \text{ Ken }, \text{ Sid }, \text{ Ned }, \text{ Ben }\}.$$ We say then that Tom (Ken, etc.) is an element of set $X$ as well as:
- Tom belongs to $X$, or
- $X$ contains Tom.
Exercise. Is a sequence a set?
We can form other sets from the same elements. We can combine those five elements into any set with any number of elements as long as there is no repetition; for example, we can create these new sets: $$\begin{array}{lll} T=\{\text{ Tom }\},\quad K= \{\text{ Ken }\},\quad S= \{\text{ Sid }\},\quad N= \{\text{ Ned }\},\quad ...\\ A=\{\text{ Tom }, \text{ Ken }\},\quad B=\{\text{ Sid }, \text{ Ned }\},\quad ...\\ Q=\{\text{ Tom }, \text{ Ken }, \text{ Sid }\},\quad ...\\ \end{array}$$
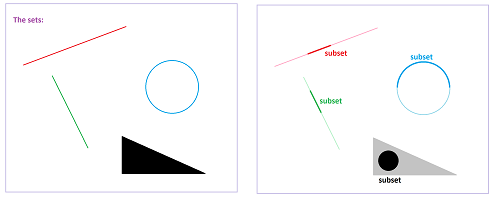
Definition. A set $A$ is called a subset of a set $X$ if every element of $A$ is also an element of $X$.
Exercise. How many subsets of $3$ elements does the set have? Hint: in how many ways can you choose three elements out of five?
We will use the following notation to convey that idea: $$T\subset X,\ K\subset X,\ A\subset X,\ Q\subset X,\ ...$$ The notation resembles the one for numbers: $1<2,\ 3<5$, etc. Indeed, a subset is, in a sense, “smaller” than the set that contains it.
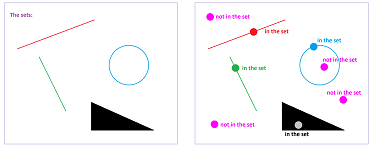
Example (geometry). We see subsets of the geometric figures in the plane:
$\square$
Sets can be infinite...
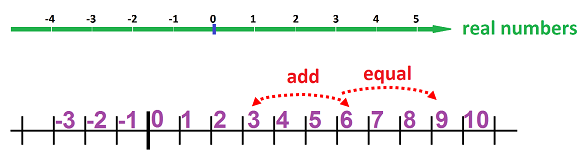
In Chapter 1, we started our study of numbers with the following two sets. We chose to speak of locations spaced over an infinite straight line associated with the integers, denoted by: $${\bf Z}=\{...,-3,-2,-1,0,1,2,3, ...\},$$ or the natural numbers: $${\bf N}=\{0,1,2,3, ...\} .$$
The set of real numbers is denoted by ${\bf R}$. It is visualized as the $x$-axis:
Of course, we know that $${\bf N}\subset {\bf Z}\subset {\bf R}.$$
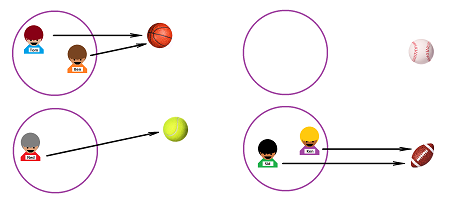
To continue with our example, suppose there is another, unrelated, set, say $Y$, the set of these four balls:
Just as $X$, set $Y$ has no structure. Just as $X$, it's just a list: $$\begin{array}{lll} Y&=\{\text{ basketball }, \text{ tennis }, \text{ baseball }, \text{ football }\}\\ &=\{\text{ football }, \text{ baseball }, \text{ tennis }, \text{ basketball }\}\\ &=\ ... \end{array}$$ We can add to or remove balls from the set creating subsets of $Y$.
Now, let's put the two sets, $X$ and $Y$, next to each other and ask ourselves, are these two sets related to each other somehow?
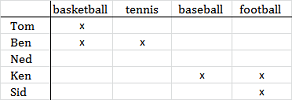
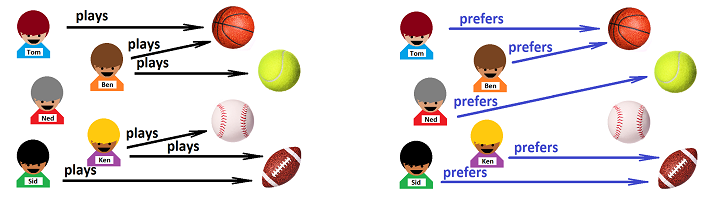
Yes, boys like sports! Let's make this idea specific. Each boy may be interested in a particular sport or he may not. For example, suppose this is what we know:
- Tom likes basketball,
- Ben likes basketball and tennis,
- Ken likes baseball and football, and
- Ben likes football.
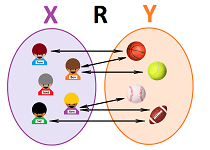
So, an element of set $X$ is related to an element of set $Y$. In order to visualize these relations, let's connect each boy with the corresponding ball by a line segment with arrows at the ends, while the two sets are arranged arbitrarily against each other:
This visualization helps us discover that Ned doesn't like sports at all... As you can see, this is a two-sided correspondence: neither of the two elements at the ends of the line comes first or second. The same applies to the sets: neither of the two sets comes first or second. In fact, we derive this:
- basketball is liked by Tom and Ben,
- tennis is liked by Ben,
- baseball is liked by Ken,
- football is liked by Ken and Sid.
We have a list of pairs:
- Tom & basketball,
- Ben & basketball,
- Ben & tennis,
- Ken & baseball,
- Ken & football,
- Ben & football.
Such a pairing is called a relation between sets $X$ and $Y$.
There may be many different relations between any two sets; let's call this one $R$:
Warning: we don't require every element to have a corresponding element in the other set.
We can also represent the relation by the following diagram: $$\begin{array}{lllll} \text{boy}& & & & &\text{Related!} \\ &\searrow & \text{relation:} & & _\text{Yes}\nearrow& \\ & & \begin{array}{|c|}\hline\quad \text{Does the boy like the ball?} \quad \\ \hline\end{array}\to & \\ &\nearrow & & & ^\text{No}\searrow& \\ \text{ball}& & & & &\text{Not related!} \\ \end{array}$$
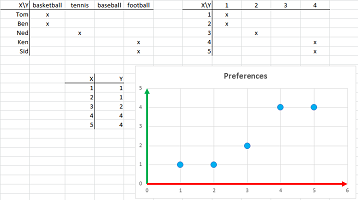
When the sets are lists, relations are tables. Let's make a table for $R$! We put the boys in the first column and the balls in the first row. If the boy likes the sport, we put a mark in the boy's row and the ball's column (left):
Or, we put the boys in the first row and the balls in the first column (right). In other words, we flip the table about its diagonal. These are two visualizations of the same relation! This is what it looks like when we use a spreadsheet instead:
Exercise. Based on the relation $R$ presented above, create a new one called, say, $S$, that relates the boys and the sports they don't like. Give an arrow and a table representations of $S$.
Exercise. Is the “subset relation” in the above example a relation?
Any combination of marks in such a table creates a relation and, conversely, a relation is nothing but a combination of marks in this table.
Throughout the early part of this book, we will concentrate on sets that consist of numbers. Even though the set of numbers does have a structure (Chapter 1), the ideas presented above still apply.
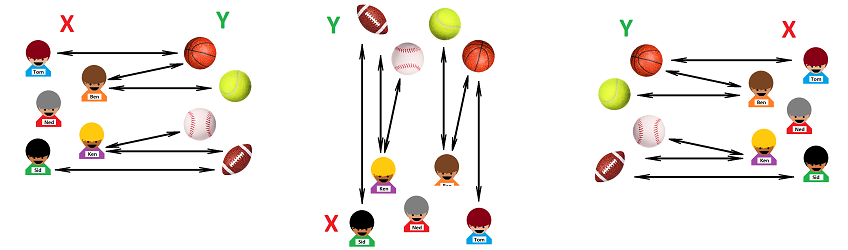
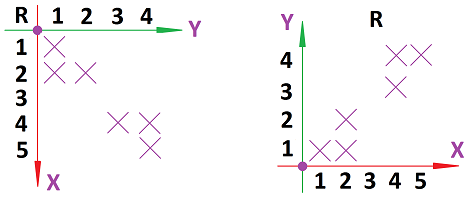
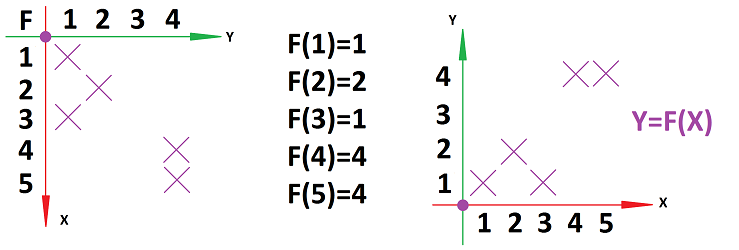
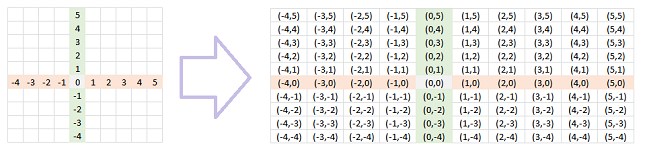
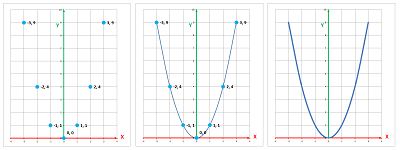
To illustrate these ideas, how about we simply rename the boys as numbers, $1-5$? And we rename the balls as numbers too, $1-4$. The table above takes this form (seen on left):
The axes are labelled to avoid confusion between the two, very different, sets. On right, the table is rotated ($90$ degrees counterclockwise) in order to present it in a more traditional way. This table is then called the graph of the relation. The two sets can still be interchanged.
Exercise. When the rows and the columns are interchanged, is there anything that is preserved?
Exercise. Finish the sentence: “This renaming of the boys is a ...”.
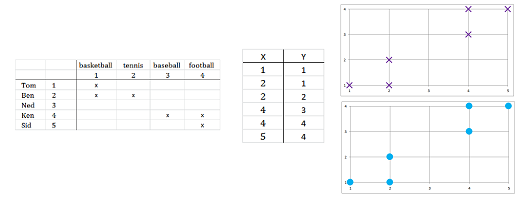
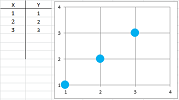
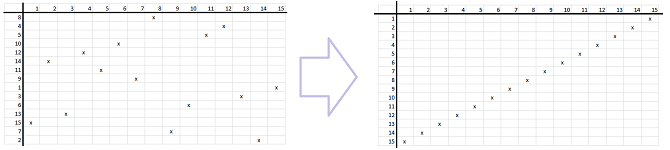
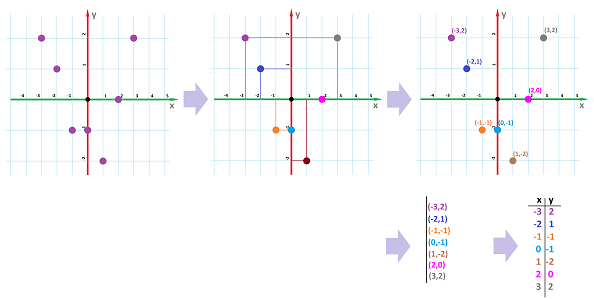
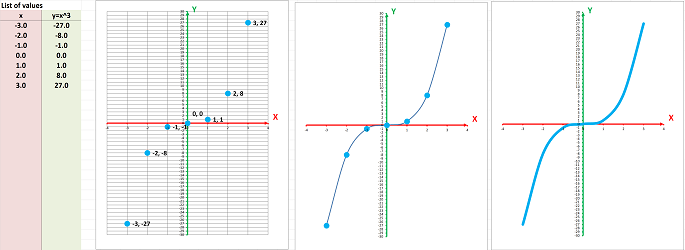
Suppose we have the elements of the sets renamed as numbers (left), then we capture the relation as a list of pairs of elements of $X$ and $Y$ (middle), and, finally, the graph of the relation can be plotted automatically by the spreadsheets. It is called a “scatter chart”:
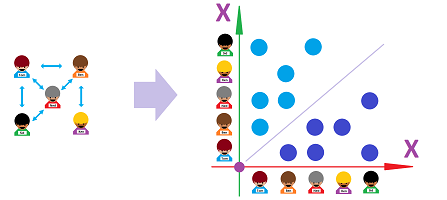
Example (networks). The plot below represents the network of friendship among the boys:
We can still represent this as a relation; we just choose the sets $X$ and $Y$ to be the same. The nature of this kind of relation isn't just two-sided, it's “symmetric”: if Tom is a friend of Ben then Ben is also a friend of Tom and vice versa. That is why each arrow in the diagram on the left is represented by two marks in the graph of the relation on the right. $\square$
Exercise. If the five boys decided to have a ping-pong tournament, what relation does it create on $X$?
Exercise. What kind of relation is produced by family relations?
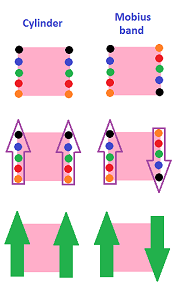
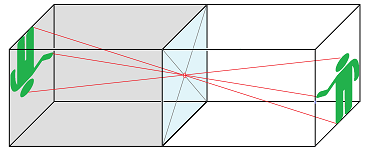
Example (gluing). We can also have relations for the sets on the plane. Suppose this set is a square. Then we can say, for example, that two points are related when then are on the opposite sides of the square. If we glue together each pair of such point, we will create a cylinder:
$\square$
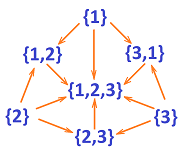
Example (subsets). The diagram below shows the subsets of the set $X=\{1,2,3\}$ and how they relate to each other:
Each arrow points from a set to another that contains it. $\square$
Exercise. Examine the above relation.
Functions
Let's go back to our running example and change the question from
- “What sports has the boy played today?”
to
- “Which sport does the boy prefer to play?”
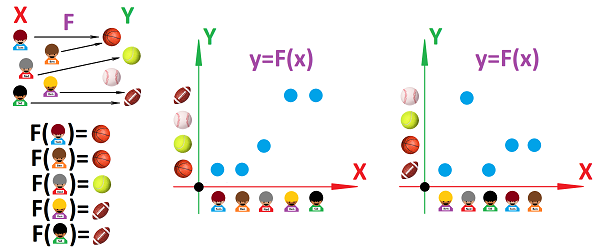
The idea is that everyone has a preference and exactly one, even Ned. This is the transition:
We had to erase one of the two arrows that start at Ben and one of the two arrows that start at Ken and we had to add an arrow for Ned.
In a relation, the two sets involved play equal roles. Instead, we now take the point of view of the boys. We will explore a new relation:
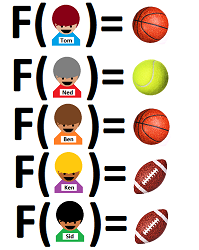
- Tom prefers basketball,
- Ben prefers basketball,
- Ned prefers tennis,
- Ken prefers football,
- Sid prefers football.
We more from our two-ended arrows (or line segments) to regular arrows:
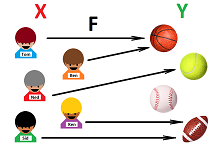
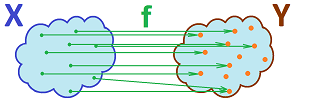
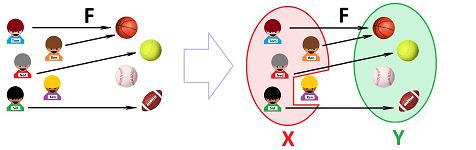
This is a special kind of relation called a function; let's call this one $F$. The two sets aren't treated equally anymore! In fact, we say that $F$ is a function from set $X$ to set $Y$. This is the common notation, which uses an arrow: $$F:X\to Y,$$ or $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccc} X& \ra{ F }& Y .\\ \end{array}$$
Each element of $X$ has only one arrow originating from it. Then, the table of this kind of relation must have exactly one mark in each row:
Our function is a procedure that answers the question: which ball does this boy prefer to play with? In fact, it answers all these questions! Conversely, a function is nothing but these answers... Each arrow clearly identifies the input -- an element of $X$ -- of this procedure by its beginning and the output -- an element of $Y$ -- as its ending. Each arrow corresponds to a row of the table (and vice versa) and is written algebraically:
Thus, a function is nothing but a list of inputs and their outputs! This is the notation: $$F(x)=y,$$ where $x$ belongs to $X$ and $y$ belongs to $Y$. The formula reads: “$F$ of $x$ is $y$”. In other words, we have: $$F(\text{ input })=\text{ output }.$$ Here is another way to write this list: $$\begin{array}{lll} F(\text{ Tom })&=\text{ basketball },\\ F(\text{ Ned })&=\text{ tennis },\\ F(\text{ Ben })&=\text{ basketball },\\ F(\text{ Ken })&=\text{ football },\\ F(\text{ Sid })&=\text{ football }.\\ \end{array}$$ This notation will be by far the most common way of representing functions.
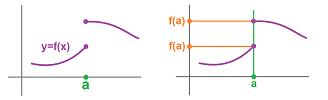
Our function -- in the form of this list or that table -- answers the question: which ball is this boy playing with? However, what if we turn this question around: which boy is playing with this ball? For example, “who is playing with the basketball”? Before answering it, we can give this question a more compact form, the form of an equation: $$F(\text{ boy })=\text{ basketball }.$$ Indeed, we need to find the inputs that, under $F$, produce this output. We answer the question by erasing all irrelevant arrows:
These are a few of possible questions of this kind along with the answers:
- Who is playing with the basketball? Tom and Ben!
- Who is playing with the tennis ball? Ned!
- Who is playing with the baseball? No-one!
- Who is playing with the football? Ken and Sid!
It seems that there are several answers to each of these questions... Or are there? “Tom” and “Ben” aren't two answers; it's one: “Tom and Ben”! Indeed, if we provide one name and not the other, we haven't fully answered the question. We can also write the answer as: $\{$ Tom, Ben $\}$. It's a set!
So, the solution to an equation $f(x)=y$ is always a set (a subset of $X$) and it may contain any number of elements including none.
Throughout the early part of this book, we will concentrate on functions the inputs and the outputs of which are numbers. Even though the set of numbers does have a structure (explained later in this chapter), the ideas presented above still apply.
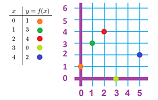
To illustrate these ideas, how about we simply rename the boys as numbers, $1-5$? And we rename the balls as numbers too, $1-4$. The table above takes this form (seen on left):
Exercise. Finish the sentence: “This renaming of the boys (and the balls) is also a ...”.
The values of $F$ have also been re-written (center). We also rotate the table counterclockwise because it is traditional to have the inputs along a horizontal line -- left to right -- and the outputs along a vertical line -- bottom to top. Then the table must have exactly one mark in each column. Every function can be represented by such a table. This table is then called the graph of the function. The arrows are still there:
We can put the data, once again, in a spreadsheet:
There is only one cross in every row!
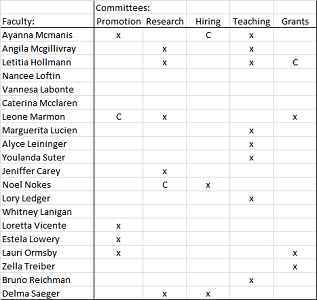
Example. Here is an example of how common spreadsheets are discovered to contain relations and functions. Below, we have a list of faculty members in the first column and a list of faculty committees in the first row. A cross mark indicates what this faculty member sits on the corresponding committee while “C” stands for “chair”.
This is a relation between these sets: $X=\{$ faculty $\}$ and $Y=\{$ committees $\}$. In addition, there is a function $F:Y\to X$ indicating the chair of the committee. $\square$
Exercise. Think of other functions present in the spreadsheet.
Exercise. Suggest functions in the situation when an employer maintains a list of employees with each person identified as a member of one of the groups or project.
Exercise. What functions do you see below?
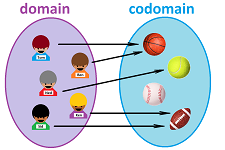
A common way to visualize the concept of set -- especially when the sets cannot be represented by mere lists -- is to draw a shapeless blob in order to suggest the absence of any internal structure or relation between the elements.
A common way to visualize the concept of a function between such sets is to draw arrows.
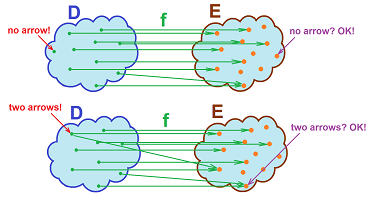
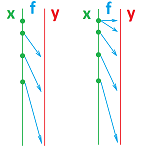
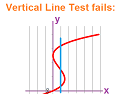
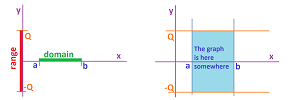
Definition. A function is a rule or procedure $F$ that assigns to any element $x$ in a set $X$, called the input set or the domain of $F$, exactly one element $y$, which is then denoted by: $$y=F(x),$$ in another set $Y$. The latter set is called the output set or the codomain of $F$. The inputs are called, collectively, the independent variable; the outputs are called, collectively, the dependent variable.
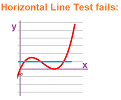
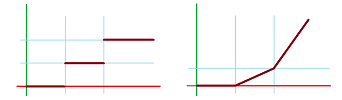
This definition fails for a relation that has too few or too many arrows for a given $x$. Below, we illustrate how the requirement may be violated, in the domain (left):
These are not functions. Meanwhile, we also see what shouldn't be regarded as violations, in the codomain (right).
Both choices for domain and codomain are equally possible.
THEOREM. Suppose $X$ and $Y$ are sets and $R$ is a relation between $X$ and $Y$: $$R:X\leftrightarrow Y.$$ Then (a) relation $R$ represents some function $F$ from $X$ to $Y$, $$F:X\to Y,$$ if and only if for each $x$ in $X$ there is exactly one $y$ in $Y$ such that $x$ and $y$ are related by $R$; and (b) relation $R$ represents some function $G$ from $Y$ to $X$, $$G:Y\to X,$$ if and only if for each $y$ in $Y$ there is exactly one $x$ in $X$ such that $x$ and $y$ are related by $R$.
When our sets are sets of numbers, the relations are often given by formulas. In that case, the above issue is resolved with algebra.
Exercise. What function can you think of from the set $X$ of the boys to the set of basic colors?
Sequences are numerical functions
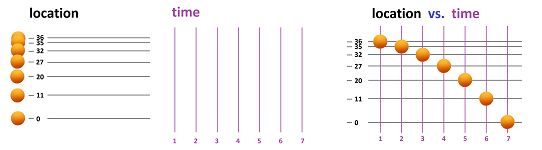
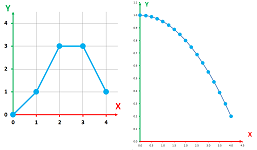
In Chapter 1, we visualized a sequence of position of a falling ball by “separating space and time”. We gave the former a real line and the latter a line of integers:
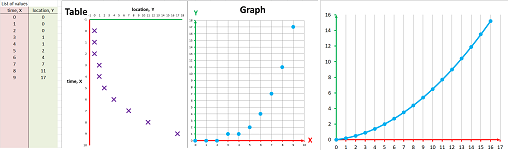
But the latter is just a subset of the former: $$\{1,2,3,4,5,6,7\}\subset {\bf R}.$$ We have, therefore, a function. Furthermore, the sequence is represented as a list of pairs of input and outputs, just as any function: $$\begin{array}{r|ll} \text{time}&\text{location}\\ n&a_n\\ \hline 1&36\\ 2&35\\ 3&32\\ 4&27\\ 5&20\\ 6&11\\ 7&0 \end{array}$$
So,
- sequences are functions with integer inputs and real outputs.
Functions with real inputs and real outputs will be called numerical functions.
Let's compare:
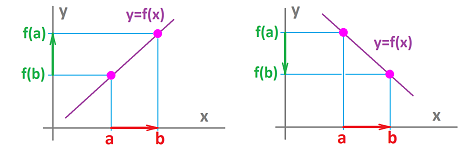
- a numerical function: the input variable is $x$, a real number; the output variable is $y=f(x)$ another real number;
- a sequence: the input variable is $n$, a natural number; the output variable is $y=a_n$ a real number.
We compare the notation too, side by side: $$\begin{array}{|ccccrcccr|} \hline &&&&&\text{ name of the function} \\ &\downarrow &&&&& \downarrow\\ &f\big(&x&\big)&&\text{ vs. }&a&_n\\ &&\uparrow&&&&&\uparrow\\ &&&&&\text{ name of the input variable}\\ \hline &&&&&\text{ value of the input variable}\\ &&\downarrow&&&&&\downarrow\\ &f\big(&3&\big)&=5&\text{ vs. }&a&_3&=5\\ &&&&\uparrow&&&&\uparrow\\ &&&&&\text{ value of the output variable} \\ \hline \end{array}$$
But is this transition -- to more a complex structure -- justified?
If $X$ is the set of time moments and $Y$ is the set of locations on the road, we can see a way to study motion! Indeed, a function $F:X\to Y$ answers a question:
- at every moment of time, where are we?
It is a function because we can't be at two locations at the same time!
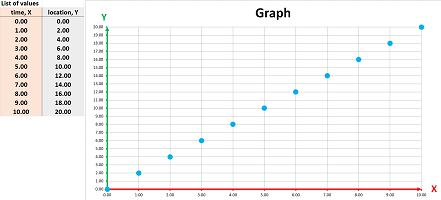
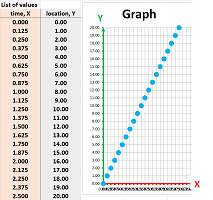
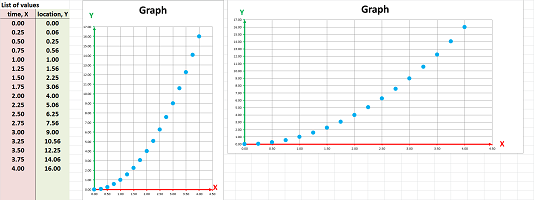
Example (driving). This is the simplest example: suppose we move to the next milestone every minute for $2$ minutes starting at the $0$ location. To make this more precise, we may ask:
- at time $x$, which milestone $y=F(x)$ did we see last?
Then the list of values of $F$ is: $$\begin{array}{l|l} \text{ time, }X& \text{ locations, }Y\\ \hline \text{ first moment }&\text{ first milestone }\\ \text{ second moment }&\text{ second milestone }\\ \text{ third moment }&\text{ third milestone } \end{array}$$ With a sequence, we would choose the domain to be: $$X=\{0,1,2\}.$$ and the codomain to be: $$Y={\bf R}.$$ Then the list becomes: $$\begin{array}{c|c} \text{ time, }X& \text{ locations, }Y\\ \hline 1&1\\ 2&2\\ 3&3 \end{array}\quad\text{ and }\quad\begin{array}{l|cc} \text{ time \ location }&1&2&3\\ \hline 1&\times \\ 2&&\times\\ 3&&&\times \end{array}$$ Finally, this is the graph of $F$:
Driving at a constant speed, i.e., we progress $2$ miles every minute:
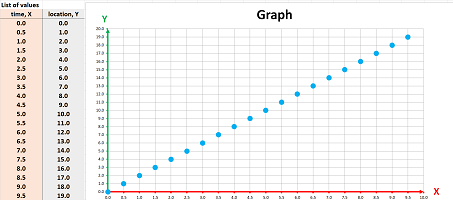
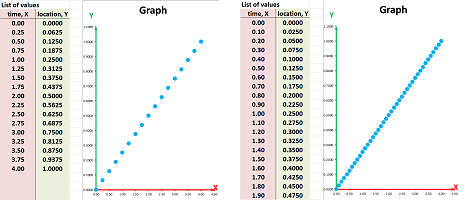
The data gives an impression that we skip milestones! So, in order to capture our motion more thoroughly, we simply introduce half-minute marks:
Is this still a sequence? Yes, if $n$ measures half-minutes. With a function, we simply keep the set of outputs $Y={\bf R}$ and change the set of inputs $X$ from $\{0,1,2,3,4,5, ...,9\}$ to $$X=\{0,.5,1,1.5,2,2.5,3, ...,8.5,9,9.5,10\}.$$ The problem is solved... until we choose to drive even faster. Driving $4$ mile per minute will require the outputs to be $$X=\{0,.25,.5,.75,1,1.25,1.5, ...,9.75,10\}.$$ And so on:
$\square$
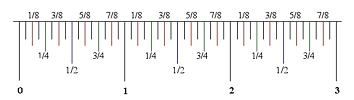
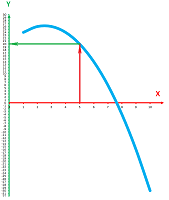
Accommodating finer and finer representations of space or time will require to continue to divide the intervals in half until it starts to look like a ruler:
The functions with the domain in the set of integers are sequences. They represent processes that progress incrementally. While this is applicable to the change of such quantities as population or money, the change of temperature or pressure is commonly assumed to be continuous! We also think of motion as a continuous progress through the physical space. This is why we apply to time the same refinement process we used for space. Then not only the outputs take their values from among all numbers but also the inputs. This way, we can fully represent the locations that we have passed through as we drive.
But how do we visualize such functions? We still represent them as sequences of pairs of numbers -- and then plot their graphs -- but with a clear understanding that some of the inputs are missing.
We insert more inputs as necessary. When there are enough of them, they start to form a curve! Or at least they do when the motion is “continuous” (Chapter 6).
Exercise. A car starts moving east from town A at a constant speed of $60$ miles an hour. Town B is located $10$ miles south of A. Represent the distance from town B to the car as a function of time.
Exercise. A car starts moving east from town A at a constant speed of $60$ miles an hour. At the same time, another car starts moving west from town A at a constant speed of $50$ miles an hour. Represent the distance between the cars as a function of time. What if the second car is moving east too? What if it starts $1$ hour late?
Example (curves). It is common to fill in the gaps in the graphs... with a stroke of a pen or with a click. For example, this is what happens to such a graph:
The result is again a curve!
$\square$
Exercise. Represent a round trip.
By choosing appropriate set $Y$ of outputs, we can model “motion” through quantities other than locations: temperature, pressure, population, money, etc.
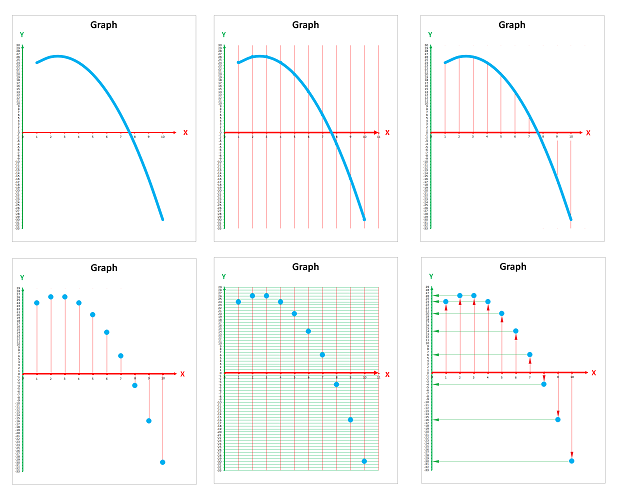
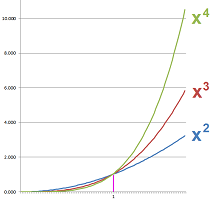
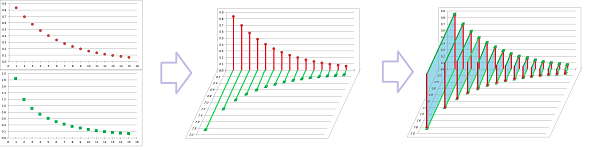
Functions and sequences both can be -- partially or fully -- represented by lists of values. In addition, they can also be defined by formulas. For example, we can match this sequence and this function: $$a_n=n^2\ \text{ and }\ f(x)=x^2.$$ Their tables of values are identical, initially: $$\begin{array}{c|c} n&y=n^2\\ \hline 0&0\\ 1&1\\ 2&4\\ 3&9\\ \vdots&\vdots \end{array}\quad\quad\quad\begin{array}{c|c} x&y=x^2\\ \hline 0&0\\ 1&1\\ 2&4\\ 3&9\\ \vdots&\vdots \end{array}$$ In contrast to the table of the sequence, the table of the function misses more, not just at the end, rows: for $x=.5,\ x=\sqrt{2},$ etc. One can also see the difference if we plot the graphs of both together:
Between any two values of the sequence, the function might have a whole interval of extra values...
Thus, every function $y=f(x)$ creates a sequence $a_n=f(n)$, but not necessarily vice versa. A “counter-example” is provided by $a_n=(-1)^n$.
Exercise. Give examples of other sequences that don't produce functions in this manner.
Exercise. The formula in the recursive definition of a sequence can be seen as a function. What are its domain and codomain?
How numerical functions emerge: optimization
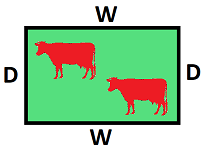
Problem: A farmer with $100$ yards of fencing material wants to build as large a rectangular enclosure as possible for his cattle.
We will initially rely entirely on our common sense and some middle school math.
Recalling some geometry, we realize that “the largest enclosure” means the one with the largest area. Now what are the best dimensions?
(1) Trial and Error. We start to randomly choose possible dimensions $w$ and $d$ of the enclosure and compute their areas with the formula: $$\text{Area }= \text{ width } \cdot \text{ depth }.$$ Then we have:
- $20$ by $20$ gives us the area of $400$ square yards,
- $20$ by $30$ gives us the area of $600$ square yards,
- $20$ by $40$ gives us the area of $800$ square yards...
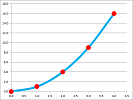
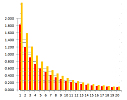
It's getting better and better! But wait... $30$ by $30$ gives us $900$! We need to collect more data. Let's speed up this process with a spreadsheet.
If $w$ stands for the width and $d$ stands for the depth, then $A$ stands for the area: $$A=w\cdot d.$$
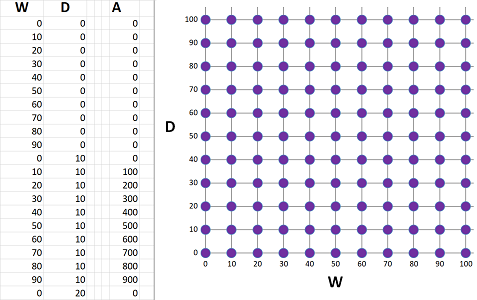
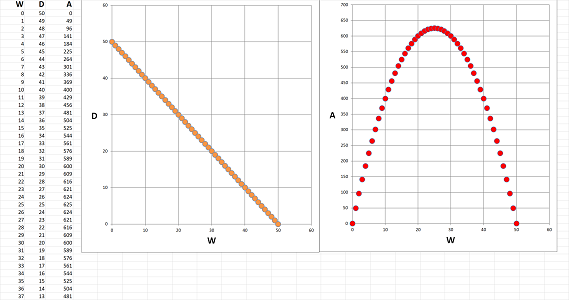
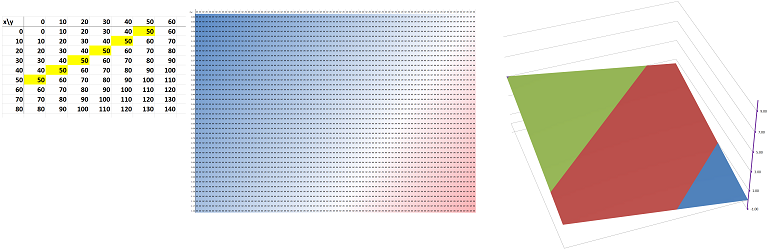
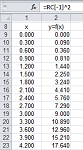
(2) Collecting data in a spreadsheet. We need to list all possible combinations -- every $10$ yards -- of a width, column $W$, and a depth, column $D$. Both values run through these $11$ numbers: $$\text{width }=0,\ 10,\ 20,\ ...,100\ \text{ and depth }=0,\ 10,\ 20,\ ...,100.$$ Together, there are $11\cdot 11=121$ possible combinations. The first challenge is to list all possible pairs of width and depths; the simplest approach is to fix one value of $w$, starting with $0$, and then start varying the value of $d$ until we reach $10$, then we set $w$ equal to $10$ and so on. Once we have them all, we also have all the areas too; we just compute the area in the third column according to the formula: $$\texttt{ =RC[-2]*RC[-1] }.$$ This is the result:
Unfortunately, we can't just look through this column and find the largest number! The reason is that we need to test whether a given combination of width and depth uses exactly $100$ yards of the fencing material. Is there a better way? To investigate, let's plot these pairs (right). Together, they form a $11\times 11$ square of possible combinations with its width and depth corresponding to the width and depth of the enclosure! We conclude that it is better to arrange these in a table than in a list.
(3) Establishing sets. We choose to consider the values in either dimension every $10$ yards via these two sets named after these two quantities: $$W=\{0,\ 10,\ ...,100\} \quad\text{ and }\quad D=\{0,\ 10,\ ...,100\}.$$
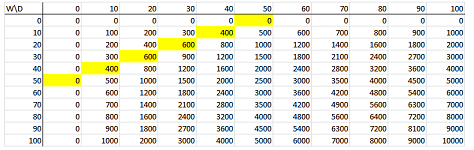
We can then compute the area of the enclosure with these dimensions according to the formula: $$\texttt{ =RC2*R2C }.$$ As a result, the table is filled with these values:
(4) Establishing a relation. A relation between the sets $W$ and $D$ is defined by:
- two numbers $w$ and $d$ are related when they form an enclosure that uses the whole $100$ yards of fencing, i.e., the perimeter $P$ is $100$:
$$P=2( w + d )=100.$$ We see its graph marked -- manually -- in yellow above and these are the only ones that are allowed. The largest areas seem to be between $20\times 30$ and $30\times 20$!
For more accurate results we need more data.
Let's go every single yard: $$W=\{0,\ 1,\ 2,\ ...,100\} \quad\text{ and }\quad D=\{0,\ 1,\ 2,\ ...,100\}.$$ Then the manual data analysis above isn't possible anymore: we have a $101\times 101$ table with $10,201$ pairs.
(5) Graph the relation. We fill the table with the values of the perimeter $P$: $$\texttt{ =2*(RC2+R2C) }.$$ We then highlight -- automatically -- the cells where the value is exactly $100$:
These are the only ones that are allowed, and they form a line.
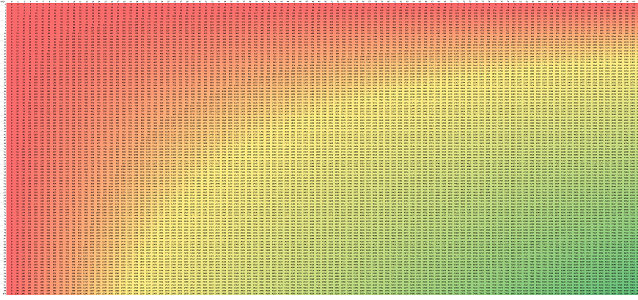
(6) Graph the areas. This time, we simply enlarge the table made for the smaller sets and fill the table with the values of the corresponding areas:
We also color -- automatically -- the cells according to their values: the values grow in the diagonal direction.
(7) Estimate maximum. Matching the two pictures, we discover again that the best result must be somewhere between the two extremes, $0\times 50$ and $50\times 0$, at the two ends of the yellow line. Maybe even somewhere halfway between $20$ and $30$. Could it be $25\times 25$?
There must be a better way... The problem is that selecting the allowable data from the whole table of pairs of $w$ and $d$ is too cumbersome. It would help if we had a direct flow of data from $w$ to $d$ to $A$.
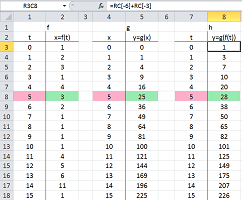
(8) Establishing functions. What if we represent the relation between $W$ and $D$ directly? In other words, what if we express $d$ in terms of $w$? We take our relation $2( w + d )=100$ and solve it for $d$: $$d=50-w.$$ Then there is exactly one $d$ for each $w$! We recognize such an explicit relation between the two sets as a function. This is its list of values ($10$ yards at a time): $$\begin{array}{l|lll} w&d\\ \hline 0&50\\ 10&40\\ 20&30\\ 30&20\\ 40&10\\ 50&0 \end{array}$$ If it's $1$ yard at time, we have $51$ rows and we put those in a new spreadsheet. The first column is for the width $w$ running through: $0,\ 1,\ 2,\ ...,50$. The second is for the depth $d$, evaluated by $$\texttt{ =50-RC[-1] }.$$
(9) Graph the functions. The graph of the depth as a function of the width is a straight line. The areas are also evaluated as before, $$\texttt{ =RC[-2]*RC[-1] },$$ and then plotted for each width:
Since there is exactly one $A$ for each $w$, this is also a function! Its graph is a curve.
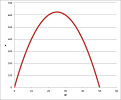
(10) Estimate maximum. Looking at the last plot, $w=25$ seems to be a clear choice with the corresponding area $A=25\cdot 25=625$ square yards.
Exercise. What happens if, instead, we express $w$ in terms of $d$?
Unfortunately, the plot has gaps! What if there is such a width that it gives us the area bigger than $625$?
We can see a new function on this spreadsheet: $A$ depends on $w$ only. What is this function? With more middle school algebra, we make this function explicit: $$A=wd=w(50-w).$$ We can now easily plot $100$ or $100,000$ points at as small increment as we like:
The answer remains the same: $$w=25,\ A=625.$$ But there are still gaps; how can we be sure? The graph of a quadratic function $A=w(50-w)=-w^2+50w$ is a parabola (Chapter 4). The “tip”, called the vertex, lies the half-way between these two points, $0$ and $50$: $$ x = \frac{ 0 + 50 }{ 2 } = 25. $$
Let's review.
We named the quantities that appear in the initial problem and then translated its sentences into algebra. The result was the following optimization problem:
- Find the values of $w$ and $d$ such that $0\le w\le 50$ and $0\le d\le 50$ so that $A=wd$ is the largest, subject to the relation $w+d=50$.
Then using the function $d=50-w$ derived from the relation to eliminate $d$ from the problem by substitution:
- Find the value of $w$ such that $0\le w\le 50$ so that $A=w(50-w)$ is the largest.
Exercise. Solve a modified problem with a river adjacent to the enclosure, which will have, consequently, three sides.
Exercise. Solve a modified problem with a new kind of enclosures required by the problem: semicircles are attached to the rectangles.
We've solved the problem, but our knowledge is much more limited when functions more complicated than quadratic polynomials are involved. Calculus (Chapter 7) will help...
Example (optimization). Find two numbers whose difference is $100$ and the product is a minimum.
Step 1. Deconstruct:
- 1. two numbers, whose
- 2. difference is $100$, and
- 3. the product is a minimum.
Translate:
- 1. introduce the “variables”: $x$ is the first number, $y$ is the second number;
- 2. constraint: $x - y = 100;$
- 3. $P$ is their product: $P=xy$, minimize $P$.
This is a math problem now.
Step 2. Eliminate the extra variables to create a function of single variable to be maximized or minimized. The constraint, an equation connecting the variables, is: $$ x - y = 100.$$ Solve the equation for $y$: $$ y = x - 100 ,$$ and eliminate $y$ from $P$ by substitution: $$ P = xy = x(x - 100). $$
Step 3. Optimize this function: $$P(x) = x^{2} - 100x .$$ The two end-points of the interval are $0$ and $100$, therefore, the “tip” (the vertex) of this parabola corresponds to: $$x = 50.$$
Step 4. Provide the answer using the original language of the problem: substitute $x$ into $y$, $$\begin{aligned} y &= x - 100 \\ &= 50 - 100 \\ &= -50. \end{aligned}$$ Answer: the two numbers are $50$ and $-50$. $\square$
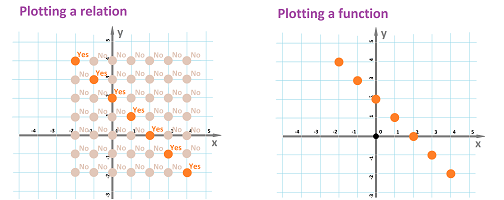
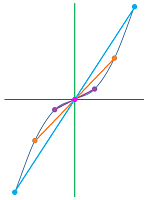
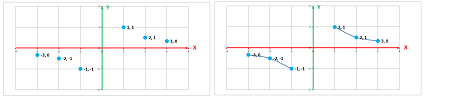
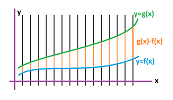
This is the summary of the analysis of the function that represents the preferences of the boys for different games presented earlier in the chapter:
The two graphs represent the same function! They only look different because we have rearranged the domain, $X$, and the codomain, $Y$. Such a move is no longer possible if we turn to numerical functions because numbers have an inherent structure, an order.
We use the tables and the graphs of functions to discover patterns in the data. However, this is only possible when the sets themselves have structure. For example, a deck of cards remains the same deck after it's been shuffled but there is also a hierarchical relation within the deck that makes all the difference to the players.
The simplest example of a set with a structure is a set of locations on a straight road. We choose milestones to be such as set. It is their order that makes it impossible to reshuffle them without losing important information. We will use that to our advantage. We visualize the set of milestones as markings on a straight line, according to their order ($1<2<3<...$):
The exactly same representation is also used for time. Every marking on a line (another line) indicates a moment of time when some repeatable event, such as a bell ring or a clock's hand passing a particular position, occurs.
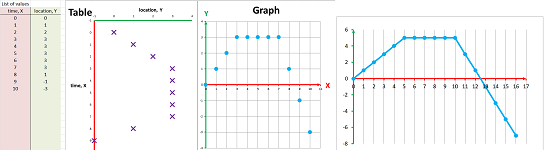
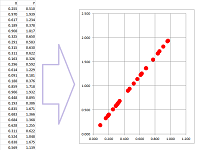
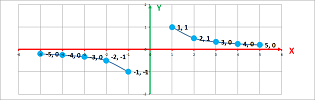
Example. The table of the function on the left has no apparent pattern... until we re-arrange the rows according to this order:
Similarly, a seemingly random list of pairs of numbers, $x$ and $y=F(x)$, produces a straight line when plotted against properly ordered numbers:
$\square$
Set building
All numerical sets in this chapter have been so far subsets of the set of real numbers ${\bf R}$. In particular, numerical sets emerge as domains and codomains of numerical functions. They may also come from solving equations.
Example (equations). Consider these:
- We face the equation $x+2=5$. After some work, we find: $x=3$.
- We face the equation $3x=15$. After some work, we find: $x=5$. Is there more?
- We face the equation $x^2-3x+2=0$. After some work, we find: $x=1$. Is that it?
- We face the equation $x^2+1=0$. After all the work, we can't find any $x$. Should we keep trying?
Here, $x$ is a label that stands for an unspecified number that is meant to satisfy this condition.
First, how do we find those $x$'s? We seek such numbers that, when they replace $x$ in the equation, we see a true statement. Then, it could simply be trial and error. For the first equation, we have:
- Is $x=1$ a solution? Plug it in the equation: $x+2=5$ becomes $(1)+2=5$. False! This is not a solution.
- Is $x=2$ a solution? Plug it in the equation: $x+2=5$ becomes $(2)+2=5$. False! This is not a solution.
- Is $x=3$ a solution? Plug it in the equation: $x+2=5$ becomes $(3)+2=5$. True! This is a solution.
- Should we stop now? Why would we? For all we know, there may be more solutions...
We never say that we have found “the” solution unless we know for sure that there is only one. $\square$
Exercise. Interpret each of these equations as a relation.
Exercise. Solve these equations: $$(a)\ x^2+2x+1=0,\quad (b)\ \frac{x}{x}=0,\quad (c)\ \frac{x}{x}=1.$$
But what does it mean to solve an equation? We have tried to find $x$ that satisfies the equation... But what are we supposed to have at the end of our work?
Let's go back to our running example of boys and balls:
It tells us what game each boy prefers. What about backward? What boys prefer each game?
- What boys prefer basketball? It's not Tom and it's not Ben; it's Tom and Ben.
- What boys prefer tennis? Ned.
- What boys prefer baseball? No-one.
- What boys prefer football? Ken and Sid.
We answer the questions by reversing the arrows.
But each question -- one for each element of the codomain $Y$ -- is also an equation:
- Find $x$ with $F(x)=$ basketball. Tom is a solution and Ben is a solution. Combined, Tom and Ben are the solutions.
- Find $x$ with $F(x)=$ tennis. Ned is the solution.
- Find $x$ with $F(x)=$ baseball. No solutions.
- Find $x$ with $F(x)=$ football. Ken and Sid are the solutions.
This is how we understand this idea:
- A solution of an equation with respect to $x$ is an element that, when put in the place of $x$ in the equation, gives us a true statement.
However, we must present all $x$'s that satisfy the equation. In other words, the answer is a set:
- The solution set of the equation $F(x)=$ basketball is $\{$ Tom, Ben $\}$.
- The solution set of the equation $F(x)=$ tennis is $\{$ Ned $\}$.
- The solution set of the equation $F(x)=$ baseball is empty.
- The solution set of the equation $F(x)=$ football is $\{$ Ken, Sid $\}$.
All of these sets are subsets of the domain $X$. It is called the solution set of the equation.
This is how we understand this idea:
- To solve an equation is to find its solution set.
This is the solution!
Next, these sets can also be presented with the so-called set-building notation: $$\{x:\ \text{ condition for } x\ \}$$ stands for the set of all $x$ that satisfy the condition. What kind of condition? Any condition will do as long as it is specific enough for us to answer the question “does $x$ satisfy it?” unambiguous. The set from which we pick $x$'s one at a time is assumed to be specified.
For example, the equations above are seen as conditions. Then, below, we list their solution sets, shown on left, that can be simplified, shown on right: $$\begin{array}{lll} \{x, \text{ boy }:\ F(x)= \text{ basketball } \} & = \{ \text{ Tom, Ben }\}, \\ \{x, \text{ boy }:\ F(x)= \text{ tennis } \} & = \{ \text{ Ned }\}, \\ \{x, \text{ boy }:\ F(x)= \text{ baseball } \} & = \{ \quad \}, \\ \{x, \text{ boy }:\ F(x)= \text{ football } \} & = \{ \text{ Ken, Sid }\}. \\ \end{array}$$ One can imagine that we simply went over the list of $X$ and test each of its elements. The third one is special.
Definition. A set with no elements is called the empty set and is commonly denoted by $\emptyset$.
Exercise. Simplify the following sets: $$\begin{array}{lll} \{x, \text{ boy }:\ \text{ his shirt is red } \},\\ \{y, \text{ ball }:\ \text{ is preferred by two boys } \},\\ \{y, \text{ ball }:\ \text{ is round } \}. \end{array}$$
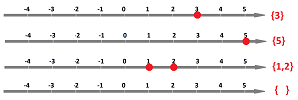
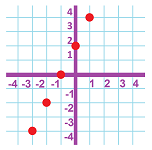
Example (solution sets). Let's take another look at the equations above assuming that the “ambient” set is the set of real numbers: $$\begin{array}{lll} \text{equation: }& \text{answer? }& \text{ solution set: }\\ \hline x+2=5 & x=3 & \{3\} \\ 3x=15 & x=5 & \{5\} \\ x^2-3x+2=0 & x=1 \text{ and...}& \{1,2\} \\ x^2+2x+1=0 & \text{ no }x?& \{\quad\} \\ \end{array}$$ This is how we visualize these four sets:
Here we use the set-building notation again on right and then, one left, we see another, simpler, representation of the set: $$\begin{array}{lll} \{x:\ x+2=5 \}&=\{3\}, \\ \{x:\ 3x=15 \}& =\{5\}, \\ \{x:\ x^2-3x+2=0 \} & = \{1,2\}, \\ \{x:\ x^2+1=0 \}& = \{\quad\}=\emptyset. \\ \end{array}$$ The simplest way to represent a set is, of course, a list. $\square$
Exercise. Solve these equations: $$x=x,\quad 1=1,\quad 1=0.$$
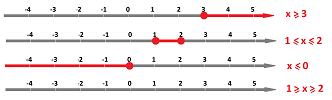
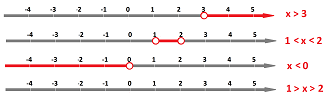
Example (inequalities), The condition in the set-building notation can also be an inequality or two: $$\begin{array}{ll} \{x,\text{ real}:& x\ge 3&\},\\ \{x,\text{ real}:&1\le x< 2&\},\\ \{x,\text{ real}:&x\le 0&\},\\ \{x,\text{ real}:&1\ge x\ge 2&\}. \end{array}$$
These are also subsets of the real number line. In contrast to a ruler, as we zoom in on the real line, we see just as many numbers as before. This is the reason why there is no such thing as the list of all real numbers, even an infinite one! Since we can't test them one by one, visualization becomes especially important. $\square$
When inequalities are involved, the (universal) set-building notation is used along with a more compact interval notation.
We start with sets of real numbers contained between two numbers. For any two real numbers $a<b$, we have: $$\begin{array}{ll} \{x:&a\le x\le b&\}&=&[a,b],&\text{closed interval;}\\ \{x:&a\le x< b&\}&=&[a,b),&\text{half-open or half-closed interval;}\\ \{x:&a< x\le b&\}&=&(a,b],&\text{half-open or half-closed interval;}\\ \{x:&a< x< b&\}&=&(a,b),&\text{open interval}. \end{array}$$ The terminology is in the right column. So,
- the bracket “[”, or “]”, is used in the interval notation when the number adjacent to it is included in the set and
- the parenthesis “(”, or “)”, is used when the number is excluded from the set.
Second, one of the ends may be infinite: $$\begin{array}{ll} \{x:&a \le x < \infty &\}&=&[a,+\infty),&\text{closed interval;}\\ \{x:&a < x < \infty&\} &=&(a,+\infty),&\text{open interval;}\\ \{x:&-\infty < x\le b&\} &=&(-\infty,b],&\text{closed interval;}\\ \{x:&-\infty < x< b&\} &=&(-\infty,b),&\text{open interval}. \end{array}$$ Infinity is always excluded from the interval because...
Warning: infinity is not a number.
Since $x$ is assumed to be a real number, inequalities that involve infinities, such as $-\infty < x$, are redundant.
The whole set of real numbers can also be seen in a similar light: $$\begin{array}{ll} \{x:&-\infty < x< +\infty&\} &=&(-\infty,+\infty)&={\bf R}.\\ \end{array}$$
Definition. These nine types of subsets of the real line are called intervals.
Example (integers). If, on the other hand, we limit ourselves to the integers here, the same inequalities won't produce intervals but lists, some of them infinite, for example: $$\begin{array}{ll} \{x,\text{ integer}:&1\le x\le 4&\}&=&\{1,2,3,4\},&\quad&\{x,\text{ integer}:&1 \le x &\}&=&\{1,2,3,4, ...\},\\ \{x,\text{ integer}:&1\le x< 4&\}&=&\{1,2,3\},&\quad&\{x,\text{ integer}:&1 < x &\} &=&\{2,3,4, ...\},\\ \{x,\text{ integer}:&1< x\le 4&\}&=&\{2,3,4\},&\quad&\{x,\text{ integer}:& x\le 4&\} &=&\{...,1,2,3,4\},\\ \{x,\text{ integer}:&1< x< 4&\}&=&\{2,3\},&\quad&\{x,\text{ integer}:& x< 4&\} &=&\{...,1,2,3\}.\\ \end{array}$$ $\square$
Exercise. Simplify: $$\{x>0:\ \text{ is an integer }\}.$$
Example (infinite point). Infinity is not a number nor a location. It is, therefore, never included in the sets that we consider. One can perceive infinity as, for example, a “point” where a long fence disappears or where two railroad tracks meet on the horizon:
We may attempt to “approach” infinity while staying within the set of numbers (Chapter 5). $\square$
For visualization, we use a little circle to indicate a missing point at the end of an interval:
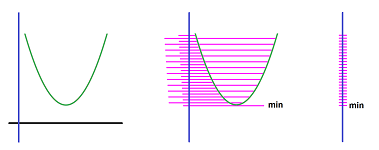
We saw in the last section optimization problems, which require finding the largest possible output of a function. But these outputs form a set! Then, on a simpler level, we just need to understand the largest and smallest elements of sets.
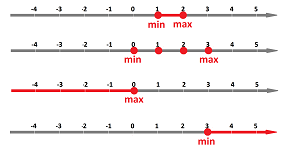
Definition. Suppose $X$ is a set of real numbers. Then the minimum of $X$ is such a number $a$ in $X$ that $$a\le x\text{ for all } x \text{ in } X.$$ The maximum of $X$ is such a number $b$ in $X$ that $$x\ge b\text{ for all } x \text{ in } X.$$ They are denoted by $\min X$ and $\max X$ respectively.
Here's a simple example: $$\min [a,b]=a,\quad \max [a,b]=b.$$
In fact, the two end-points of these two intervals are the max and min of the set.
Exercise. Explain the grammar in the definition, why “the”?
What about these: $$\min (a,b)=?,\quad \max (a,b)=?$$ These aren't $a$ and $b$ because they don't belong to the set anymore. There is no maximum of minimum!
Example. An even simpler case is a list of numbers arranged in increasing order; then the task is easy: $$\min \{-1,3,7,12,16\}=-1,\quad \max \{-1,3,7,12,16\}=16.$$ We just examine the list and pick the largest or the smallest element. However, if the list grows infinite and unbounded, such as: $$X=\{1,2,3,4,5,...\},$$ there is, once again, no maximum! We can't say that the maximum is the infinity because... $\square$
Warning: infinity is not a number.
A set may have no maximum or no minimum! The whole set of real numbers ${\bf R}$ is such a set.
In the example, the best candidate for maximum doesn't belong to the set! Then, the question what is the largest value? may have to wait until we answer is there the largest value? This is how we approach this issue: if $2$ is not the maximum of $X=(1,2)$ then what is it?
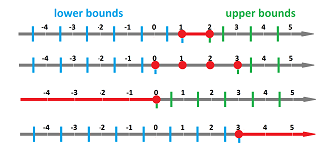
Definition. Suppose $X$ is a set of real numbers. Then a number $A$ (it doesn't have to belong to $X$) is called a lower bound of $X$ if $$A\le x\text{ for all } x \text{ in } X.$$ A number $B$ (it doesn't have to belong to $X$) is called an upper bound of $X$ if $$B\ge x\text{ for all } x \text{ in } X.$$ A set that possesses both lower and upper bounds is called bounded, otherwise unbounded.
Example. Then these are bounded: $$\{-1,3,7,12,16\},\ [a,b],\ (a,b),$$ and these are unbounded: $${\bf R},\ {\bf Z},\ \{1,2,3,4,5,...\}.$$ $\square$
Exercise. Show that if $X$ is bounded, it is a subset of an interval $[A,B]$, where $A$ and $B$ are any of its lower and upper bounds respectively.
Exercise. What are the max, min, and bounds of the empty set? What about ${\bf R}$?
Exercise. Solve the following equations: $$(a)\ x^2+2x+1=0,\quad (b)\ x^2=-1,\quad (c)\ x^2=1,\quad (d)\ \frac{x}{x}=1,\quad (e)\ \frac{x}{x}=0.$$
The $xy$-plane: where graphs live...
A relation or a function deals with two sets of numbers: the domain $X$ and the codomain $Y$. That's why we need two axes. How do we arrange them? We can use the method presented above: putting $X$ and $Y$ side-by-side and connecting them by arrows:
If $X$ is infinite, however, we would need infinitely many arrows. Is there a better way? We already know another approach: table and graphs. Instead of side-by-side, we place $X$ horizontally and $Y$ vertically.
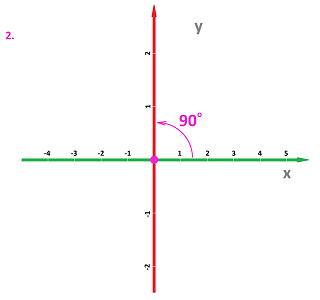
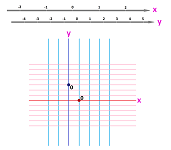
We start with a real line ${\bf R}$, or the $x$-axis, again. That's where the real numbers live and now $X$ and $Y$ are subsets of ${\bf R}$. So, we will need two copies of the real line. We give them special names:
- the $x$-axis and
- the $y$-axis.
Just as the inputs and the outputs of a function have typically nothing to do with each other (such as time vs. space, or space vs. temperature), the two axes may have different unit segments:
That's step 1.
Next, we make a step toward the table we need and arrange the two coordinate axes as follows:
- the $x$-axis is usually horizontal, with the positive direction pointing right, and
- the $y$-axis is usually vertical, with the positive direction pointing up.
Usually, the two axes are put together so that their origins merge. That's step 2.
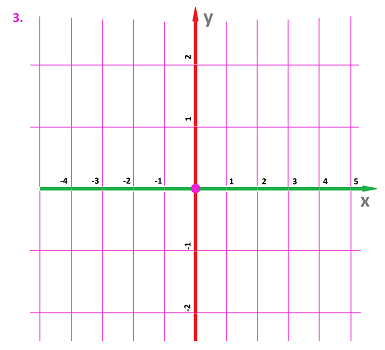
Finally, we use the marks on the axes to draw a rectangular grid.
That's step 3, and we have what we call the Cartesian plane or simply the $xy$-plane. As it is made from a combination of two copies of ${\bf R}$ and is often denoted by ${\bf R}^2$.
The idea that the real line is like a ruler leads to the idea that the $xy$-plane is like ruled paper:
However, we also include the points away from the marks.
Example (graphs). In the context of plotting graphs, it is frequently the case that the relative dimensions of $x$ and $y$ are unimportant; then the $xy$-plane can be resized arbitrarily and disproportionately. The graphs change! The chart in this spreadsheet shows how different the graph of the same function might look:
Such resizing will turn squares into rectangles and circles into ovals:
This fact imposes important limits on how well the graph visualizes the function. The size, of course, doesn't matter. The angles might be telling us nothing; for example, the inclination -- up or down -- of the graph cannot disappear but its steepness can change. We can't, therefore, say that this line is “steep” but only that it is “steeper” than another one plotted on the same coordinate plane.
In this context, it is also often acceptable to have the origins of the two axes misaligned or even absent:
$\square$
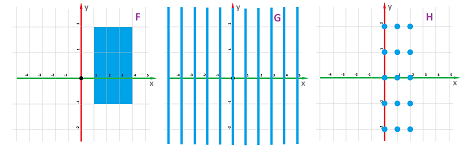
Example. Below, we point out on the plane the locations of the graphs of any three functions with these domains and codomains: $$F:[1,4]\to [-1,2],\quad G:{\bf Z}\to {\bf R},\quad H:\{0,1,2\}\to {\bf Z}.$$
$\square$
The idea of the Cartesian coordinate system is similar to the one for the real line but this time there are two axes and two coordinates. We use the above set-up to produce a correspondence: $$\begin{array}{|c|}\hline \quad \text{location } P\ \longleftrightarrow\ \text{ a pair of numbers } (x,y) ,\quad \\ \hline\end{array}$$ that works in both directions.
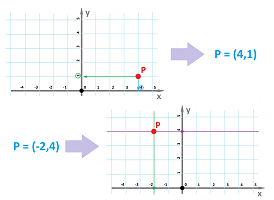
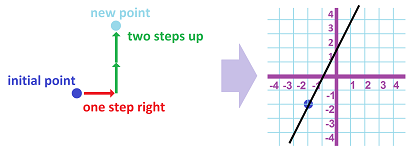
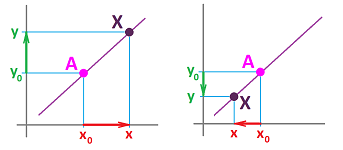
For example, suppose $P$ is a location on the plane. We then draw a vertical line through $P$ until it intersects the $x$-axis. The mark, $x$, of the location where they cross is the $x$-coordinate of $P$. We next draw a horizontal line through $P$ until it intersects the $y$-axis. The mark, $y$, of the location where they cross is the $y$-coordinate of $P$. On the flip side, suppose $x$ and $y$ are numbers. First, we find the mark $x$ on the $x$-axis and draw a vertical line through this point. Second, we find the mark $y$ on the $y$-axis and draw a horizontal line through this point. The intersection of these two lines is the corresponding location $P$ on the plane.
The notation is as follows: $$\big(\quad x-\text{coordinate}\quad, \quad y-\text{coordinate}\quad\big).$$ Thus, every point on the $xy$-plane is, or can be, labelled with a pair of numbers:
Warning: the notation $(a,b)$ is, unfortunately, the same for a point on the $xy$-plane with coordinates $a$ and $b$ and for an open interval from $a$ to $b$.
Once the coordinate system is in place, it is acceptable to think of locations as pairs of numbers and vice versa. In fact, we can write: $$P=(x,y).$$
It is important to realize that what we are dealing with is a set too! It is the set of all pairs of real numbers: $${\bf R}^2=\{(x,y):\ x\text{ real},\ y\text{ real }\}.$$ The $xy$-plane is just a visualization of this set. Below we consider some of its simplest subsets.
Example (lines). One can think of the $xy$-plane as a stack of lines, vertical or horizontal, each of which is just a copy of one of the axes:
We can use this idea to reveal the internal structure of the coordinate plane.
- (a) If $L$ is a line parallel to the $x$-axis, then all points on $L$ have the same $y$-coordinate. Conversely, if a set $L$ of points on the $xy$-plane consists of all points with the same $y$-coordinate, $L$ is a line parallel to the $x$-axis.
- (b) If $L$ is a line parallel to the $y$-axis, then all points on $L$ have the same $x$-coordinate. Conversely, if a set $L$ of points on the $xy$-plane consists of all points with the same $x$-coordinate, $L$ is a line parallel to the $y$-axis.
Then, we have a compact way to represent these two lines:
- horizontal: $y=3$, and
- vertical: $x=2$.
$\square$
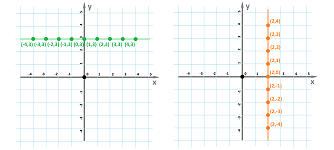
The most important subsets of the plane will be initially the graphs of relations and functions. For example, a sequence of numbers produces a sequence of points on the plane:
Linear relations
Recall that a relation between two sets is any pairing of their elements. This time, the sets are sets of numbers and the condition to be checked is an equation: $$\begin{array}{lllll} \text{sets:}& &\text{elements:}& & & & &\text{} \\ X\subset{\bf R} & \to & x& & & & \text{Related!} \\ &&&\searrow & \text{relation:} & _\text{Yes}\nearrow& \\ &&& & \begin{array}{|c|}\hline\quad x+y=2? \quad \\ \hline\end{array}\to & \\ &&&\nearrow & & ^\text{No}\searrow& \\ Y\subset{\bf R} & \to &y& & & & \text{Not related!} \\ \end{array}$$ So, a numerical relation processes a pair of numbers $x$ and $y$ and tells: related or not related, Yes or No.
Warning: Just because both sets are numbers (for example, $X={\bf R}$ and $Y={\bf R}$), we shouldn't think of the relation as one of a set with itself.
Example (enclosure). This is how we visualized a relation earlier in this chapter. Recall how, in the case of the farmer, his enclosure has width $x$ and height $y$ and there are related -- because of the amount of material for the fence available -- by a relation: $$x+y=50.$$ To speed up the analysis, we pre-computed all values of $x+y$ for all eligible $x$ and $y$. The result is a table filled by means of the following spreadsheet formula: $$\texttt{ =RC2+R2C }.$$ It was easy in a small table to color the cells with value of $x+y$ equal to $50$ (left); they form a line:
We furthermore colored a very large array of cells (middle): the color of the $(x,y)$ cell is determined by the value of $x+y$. The linear pattern still seems conceivable. The value of $x+y$ can also be visualized as the elevation at that location on the plane (right). $\square$
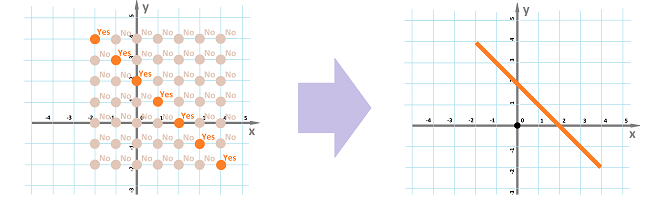
In general, plotting the graph of a numerical relation means processing a pair of numbers $(x,y)$, one at a time, and producing an output, which is: related or not related, Yes or No, a point or no point. For example: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &&& & & &\text{outcome:} \\ &&& & & &\text{plot point } (x,y) \\ \text{plane:} & &\text{pair:} & & \text{relation:} & _\text{Yes}\nearrow& \\ {\bf R}^2&\to&(x,y) & \to & \begin{array}{|c|}\hline\quad x+y=2? \quad \\ \hline\end{array}\to & \\ &&& & & ^\text{No}\searrow& \\ &&& & & &\text{don't plot anything} \\ \end{array}$$ We can try to do this by hand, one at a time: $$(0,0)\to\text{ No!}\quad(1,0)\to\text{ No!}\quad(1,1)\to\text{ Yes!}\ ...$$ It takes a lot of tries to produce a picture that reveals a pattern (left):
On right, we show our conjecture about the graph of the relation; it looks like a straight line!
Exercise. Show that the equation $2x+2y=4$ represents the same relation!
We saw in the last section two examples of relations the graphs of which are lines:
- the relation $y=c$ produces a horizontal line because point $(x,y)$ is to be plotted as long as $y=c$ (there is no restriction on $x$);
- the relation $x=a$ produces a vertical line because point $(x,y)$ is to be plotted as long as $x=a$ (there is no restriction on $y$).
In summary, suppose $R$ is a relation between two sets $X$ and $Y$ of real numbers. Then the graph of $R$ is the set of all points on the $xy$-plane such that $x$ and $y$ are related by $R$. This relation is, typically, an equation, and, in this case, “most” of the points on the plane won't satisfy it. Those that do will likely to form a curve.
We start with the simplest, and the most common, kind.
THEOREM. The graph of any linear relation, i.e., $$Ax+By=C,$$ with either $A$ or $B$ not equal to zero, is a straight line.
Exercise. What is the graph when $A=B=0$? Hint: there are two cases.
It is called an implicit equation of the line. When we represent the line by a function (next section), the equation becomes explicit.
The ideas of linear algebra have a very humble beginning.
Example (linear equation). Suppose we have a type of coffee that costs $\$3$ per pound. How much do we get for $\$60$?
The setup is the following. Let $x$ be the weight of the coffee. Since the total price is $60$, we have a linear equation: $$3x=60.$$ We solve it: $$x=\frac{60}{3}=20.$$ $\square$
The operations are very simple, and the complexity comes from elsewhere: the number of variables.
Example (mixtures). Suppose we have the Kenyan coffee that costs $\$2$ per pound and the Colombian coffee that costs $\$3$ per pound. How much of each do you need to have $6$ pounds of blend with the total price of $\$14$?
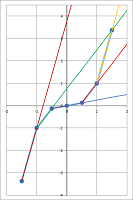
The setup is the following. Let $x$ be the weight of the Kenyan coffee and let $y$ be the weight of Colombian coffee. Since the total weight is $6$, we have a linear relation between $x$ and $y$: $$x+y=6.$$ Since total price of the blend is $\$ 14$, we have another linear relation between $x$ and $y$: $$2x+3y = 14.$$ The graphs of the relations are these lines:
Then, for a combination of weights $x$ and $y$ to satisfy both of the requirements, the point $(x,y)$ has to belong to both of the lines! The solution, therefore, is the point that they have in common, called their intersection (Chapter 3). This point can be guessed to be $(x,y)=(4,2)$. This can be confirmed by substituting the two numbers $x=4,\ y=2$ into the two relations.
An algebraic solution is as follows. From the first equation, we derive: $y=6-x$. Then substitute into the second equation: $2x+3(6-x)=14$. Solve the new equation: $-x=-4$, or $x=4$. Substitute this back into the first equation: $(4)+y=6$, then $y=2$.
Such a problem is called a system of linear equations (Chapter 23): $$\begin{cases} x&+y &= 6 ,\\ 2x&+3y &= 14. \end{cases}$$ We can collect the data in tables as follows: $$\begin{array}{|ccc|} \hline 1\cdot x&+1\cdot y &= 6 \\ \hline 2\cdot x&+3\cdot y &= 14\\ \hline \end{array}\leadsto \begin{array}{|c|c|c|c|c|c|c|} \hline 1&\cdot& x&+&1&\cdot& y &=& 6 \\ 2&\cdot& x&+&3&\cdot &y &=& 14\\ \hline \end{array}\leadsto\left[ \begin{array}{cc|c} 1&1&6 \\ 2&3&14\\ \end{array}\right].$$ The $2$-by-$2$ part on the left of the resulting table is made of the coefficients of $x$ and $y$ in the equations. It is called a matrix. $\square$
Exercise. Set up a system of linear equations -- but do not solve it -- for the following problem: “An investment portfolio worth $\$1,000,000$ is to be formed from the shares of: Microsoft - $\$5$ per share and Apple - $\$7$ per share. If you need to have twice as many shares of Microsoft than Apple, what are the numbers?”
Exercise. Set up, do not solve, the system of linear equations for the following problem: “One serving of tomato soup contains $100$ Cal and $18$ g of carbohydrates. One slice of whole bread contains $70$ Cal and $13$ g of carbohydrates. How many servings of each should be required to obtain $230$ Cal and $42$ g of carbohydrates?”
Exercise. Solve the system of linear equations: $$\begin{cases} x-y&=2,\\ x+2y&=1. \end{cases}$$
Exercise. Solve the system of linear equations and geometrically represent its solution: $$\begin{cases} x-2y&=1,\\ x+2y&=-1. \end{cases}$$
Exercise. Geometrically represent this system of linear equations: $$\begin{cases} x-2y&=1,\\ x+2y&=-1. \end{cases}$$
Exercise. What if there is a third type of coffee in the example, say, $\$ 4$ per pound?
Relations vs. functions
It is crucial that graphs are sets too; they are subsets of ${\bf R}^2$. In fact, we can still use the set-building notation: $$\{(x,y): \ \text{condition on } x,\ y\}.$$ This condition, just as before, is often an equation; for example, $$\{(x,y): \ x^2+y^2=1\}.$$ Because of the indirect nature of the definition of this set, plotting the graph of a numerical relation is cumbersome: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &&& & & &\text{outcome:} \\ &&& & & &\text{plot point } (x,y) \\ \text{plane:} & &\text{pair:} & & \text{relation:} & _\text{Yes}\nearrow& \\ {\bf R}^2&\to&(x,y) & \to & \begin{array}{|c|}\hline\quad x+y=2? \quad \\ \hline\end{array}\to & \\ &&& & & ^\text{No}\searrow& \\ &&& & & &\text{don't plot anything} \\ \end{array}$$
What else can we do?
Example (lines). This is how we visualized a relation earlier in this chapter. We pre-computed all values of $x+y$:
- each value of $x+y$ is placed at the location $(x,y)$.
We filled a spreadsheet with these values and then we examined the patterns. We discovered them to be linear:
But it was a conjecture... $\square$
We proved that the graph of any linear relation, i.e., $$Ax+By=C,$$ with either $A$ or $B$ not equal to zero, is a straight line. It is called an implicit equation of the line. When we represent the line by a function (below), the equation becomes explicit; all we need is to solve for $x$ or for $y$.
THEOREM. A linear relation between the sets $X={\bf R}$ and $Y={\bf R}$, $$Ax+By=C,$$ may be represented by a function, called a linear function, as follows,
- (a) a function $F:X \to Y$, when $B\ne 0$, given by:
$$y=F(x)=-\frac{A}{B}x+\frac{C}{B};$$ and
- (b) a function $G:Y\to X$, when $A\ne 0$, given by:
$$x=G(y)=-\frac{B}{A}y+\frac{C}{A}.$$
Indeed, every function is a relations but not every relation is a function, but sometimes it is a function... or two!
Example. In the relation $x+y=20$ above, we have $A=1$ and $B=1$, so we can do both: $$y=-x+20\ \text{ and }\ x=-y+20.$$ In the relation $y=3$, we have $A=0$ and $B=1$; this is the former case and the function is constant: $$F(x)=3.$$ In the relation $x=2$, we have $A=1$ and $B=0$; this is the latter case and the function is constant: $$G(y)=2.$$ $\square$
Exercise. Find all linear functions is these linear relations: $3x-2y=2$, $2x=3$, $-y=7$.
Exercise. Prove the theorem.
Exercise. What lines are not included in case (a)? case (b)?
Transitioning to functions makes the plotting task much easier.
Indeed, the $49$ computations are reduced to just $7$: $$\begin{array}{r|r} x&y=-x+2\\ \hline -2&4\\ -1&3\\ 0&2\\ 1&1\\ 2&0\\ 3&-1\\ 4&-2 \end{array}$$
In general, instead of having to run through a whole plane of $(x,y)$'s -- for relations, we only need to run through a line of $x$'s -- for functions. We also observe that, since there can be only one point of the graph of a function above each $x$, the graph of a function must be one-point thick, just like a curve...
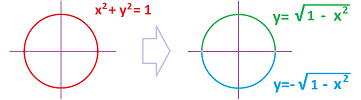
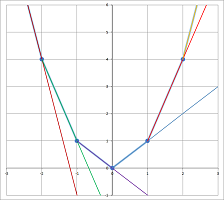
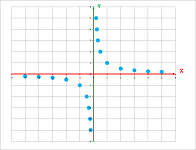
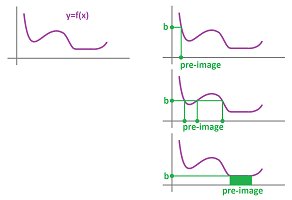
Example (circles). Let's consider a more complex relation: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} & & & & &\text{output:} \\ & & & & &\text{plot point } (x,y) \\ \text{input:} & & \text{relation:} & & _\text{Yes}\nearrow& \\ (x,y) & \mapsto & \begin{array}{|c|}\hline\quad x^2+y^2=1? \quad \\ \hline\end{array}\to & \\ & & & & ^\text{No}\searrow& \\ & & & & &\text{don't plot anything} \\ \end{array}$$ We quickly run through a few: $$(0,0)\to \text{No!}\quad (1,0)\to \text{Yes!}\quad(1,1)\to \text{No!}\quad(0,1)\to \text{Yes!}\quad...$$ Let's arrange the initial results in a $2\times 2$ square around the origin: $$\text{locations: }\begin{array}{|lll|} \hline (-1,1)&(0,1)&(1,1)\\ (-1,0)&(0,0)&(1,0)\\ (-1,-1)&(0,-1)&(1,-1)\\ \hline \end{array},\quad\text{relation: } \begin{array}{|ccc|} \hline \text{No}&\text{Yes}&\text{No}\\ \text{Yes}&\text{No}&\text{Yes}\\ \text{No}&\text{Yes}&\text{No}\\ \hline \end{array},\quad\text{graph: } \begin{array}{|ccc|} \hline \circ&\bullet&\circ\\ \bullet&\circ&\bullet\\ \circ&\bullet&\circ\\ \hline \end{array}$$ Is this a curves? We seem need many more values to get an idea! Unfortunately, when we try to go $.5$ at a time, $$x=-1.5,\ -.5,\ .5,\ 1.5 \ \text{ and }\ y=-1.5,\ -.5,\ .5,\ 1.5,$$ we just produce No's exclusively.
We try another approach to visualize the graph of a relation. Just as with the linear relations in the last section, we consider many relations at the same time: $$x^2+y^2=k,$$ with variable $k$'s. We create a table of the values of this expression in a spreadsheet with the formula: $$\texttt{ =RC1^2+R1C^2}.$$ We then color the cells:
The small values of $k$ are in blue and the large are in red. Our interest is $k=1$ and, therefore, the points in blue are too close to the origin and those in red are too far. The circular pattern is also clear. The pattern seems to be made from concentric circle with the radius varying with $k$:
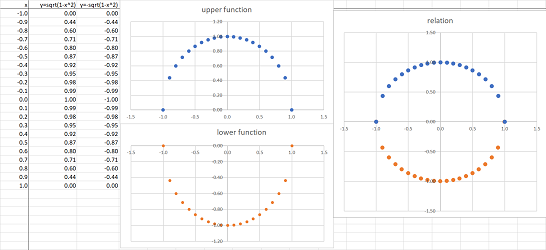
To justify the last conclusion, let's ask, is there a function that represents this relation? Let's solve for $y$. We have: $$y=\pm\sqrt{1-x^2}.$$ But this is not a function; indeed, input $x=0$ produces two outputs, $y=1$ and $y=-1$. But what does this equation represent? This is just a new relation! We have replaced the original relation,
- $x$ and $y$ are related when $x^2+y^2=1$,
with the following relation:
- $x$ and $y$ are related when $y=\pm\sqrt{1-x^2}$.
It is just a new representation of the original relation.
Here is another way to write it:
- $x$ and $y$ are related when $y=\sqrt{1-x^2}$ or $y=-\sqrt{1-x^2}$.
How does this help? An examination reveals that we have two separate functions. We can then produce a table of values for each for a large number of $x$'s between $-1$ and $1$. And we can plot their graphs from this data, separately:
Either graph is an arc and together they form a circle:
$\square$
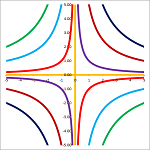
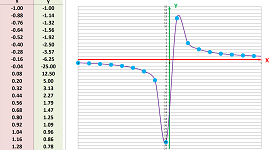
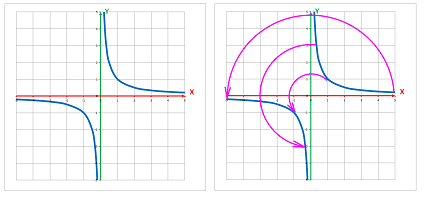
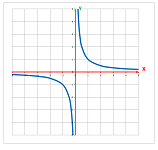
Example (hyperbolas). We color the cells of an array according to the values of $$xy=k.$$
This is what the graphs of these the relations look like plotted for various $k$'s; they are curves called hyperbolas (Chapter 4):
They are the graphs of the functions that come from solving the equation for $y$ or $x$: $$y=\frac{k}{x}\ \text{ and }\ x=\frac{k}{y}.$$ $\square$
Exercise. Each hyperbola seems to consist of two branches. Justify this observation.
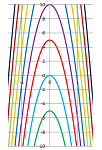
Example (parabolas). We color the cells of an array according to the values of $$y-x^2=k$$ plotted for various $k$'s:
This is what the graphs of these the relations look like plotted for various $k$'s; they are curves called parabolas (Chapter 4):
They are the graphs of the functions that come from solving the equation for $y$: $$y=x^2+k.$$ $\square$
Exercise. What if we solve for $y$ instead?
Exercise. Visualize the relation $2x^2+y^2=3$.
Even with a computer, trying to find every point on the whole $(x,y)$-plane that satisfies a given relation is like looking for a needle in a haystack. In contrast, functions produce the “allowed” pairs $(x,y)$ automatically, without needing to test each of them. Simply plug in a value, $x$, and the function will give you its mate, $y$.
Remember, all functions are relations but not all relations are functions:
This means that what we have said about relations will apply to functions, but we will be able to say much more about the latter...
A function as a black box
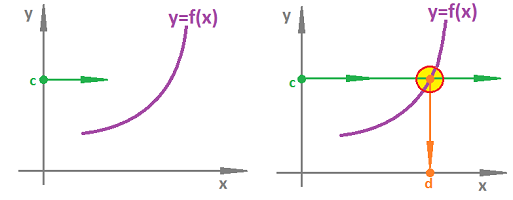
Functions are explicit relations. Indeed, the two variables are still related to each other, but this relation is now unequal: the output is dependent this is a function. That is why we say that the input is the independent variable while the output is the dependent variable.
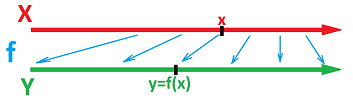
A function is a black box: something comes in and something comes out as a result. Like this: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\blacksquare\blacksquare\blacksquare \\ \hline\end{array} & \mapsto & \text{output} \end{array}.$$ The only rule is that the same input produces the same output. For example, a vending machine will provide you with the item the code of which you have entered (if sufficient funds are inserted).
In the case of numerical functions, both are numbers. The black box metaphor suggests that while some computation happens inside the box, what it is exactly may be unknown: $$\begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ \text{income} & \mapsto & \begin{array}{|c|}\hline\quad \text{IRS} \quad \\ \hline\end{array} & \mapsto & \text{tax bill}\ . \end{array}$$ How things happen might be even unimportant; what's important is the rule a function has to follow: one $y$ for each $x$. For example, if you don't know how this function is computed, you can ask someone to do it for you: $$\begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ x & \mapsto & \begin{array}{|c|}\hline\quad \cos \quad \\ \hline\end{array} & \mapsto & y \text{}&. \end{array}$$
If we are able to peek inside, we might see something very complex or something very simple: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ multiply by }3 \\ \hline\end{array} & \mapsto & \text{output }\ . \end{array}$$
A function is what a function does! It may be simply a sequence of instructions
Example (flowcharts). For example, for a given input $x$, we do the following consecutively:
- add $3$,
- multiply by $2$,
- square.
Such a procedure can be conveniently visualized as a “flowchart”:
For example, if the input is $x=1$ then we acquire three more numbers in this order: $$1\ \to\ 1+3=4\ \to\ 4\cdot 2=8 \ \to\ 8^2=64.$$ It can also be called an algorithmic representation.
Here is the algebra of what is going on inside of each of the boxes: $$\begin{array}{ccc} x & \mapsto & \begin{array}{|c|}\hline\quad x+3 \quad \\ \hline\end{array} & \mapsto & y & \mapsto & \begin{array}{|c|}\hline\quad y\cdot 2 \quad \\ \hline\end{array} & \mapsto & z & \mapsto & \begin{array}{|c|}\hline\quad z^2 \quad \\ \hline\end{array} & \mapsto & u \end{array}.$$ We have introduced intermediate variables for reference. Note how the names of the variables match, so that we can proceed to the next step. A sequence of algebraic steps of this process is as follows: $$\begin{array}{lll} x&\to&x+3&=&y\\ &&&\to & y\cdot 2&=&z\\ &&&&&\to&z^2&=&u. \end{array}$$ $\square$
Exercise. Describe the function that computes the sales tax of $5\%$.
Exercise. Describe the function that computes the discount of $10\%$.
Warning: such a sequence of commands might have forks in order to represent more complex functions.
Thus, we represent a function diagrammatically as a box that processes the input and produces the output: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ x & \mapsto & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y \end{array}.$$ Here, $f$ is the name of the function (in fact, “$f$” stands for “function”). In this example, the function is unspecified. We make it specific by describing how it works. Some specific function are given specific names made of letters and symbols, such as these:
- $\sqrt{(\quad)}$ for the square root,
- $\exp (\quad )$ or $e^{(\quad)}$ for the exponential function,
- $\sin (\quad ) $ for the sine, etc.
Numerical functions come from many sources and can be expressed in different forms:
- a list of instructions (an algorithm),
- an algebraic formula,
- a list of pairs of inputs and outputs,
- a graph,
- a transformation.
We will be transitioning from one to the next as needed with the exception of the last item which is postponed until the next chapter.
An algorithm is commonly a list of instructions given to a computer, i.e., a program. It may be advantageous to have a function to be handled by a person to be given in the form of a formula. The person may appreciate a more compact form that allows to notice patterns, simplify, and further manipulate the function.
An algebraic representation is exemplified by $y = x^2$. In order to properly introduce this as a function, we give it a name, say $f$, and write: $$f(x)=x^2.$$ Let's examine this notation. The letters used in the left-hand side are all names! $$\begin{array}{r|ccc} &y&=&f&( &x&)&=&x^2\\ &\uparrow&&\uparrow&&\uparrow&&&\uparrow\\ \text{name: }&\text{dependent }&&\text{function }&&\text{independent }&&&\text{independent}\\ &\text{variable }&&\text{ }&&\text{variable }&&&\text{variable} \end{array}$$ The names are mostly arbitrary. They have to vary when there is more than just one function involved, for example: $$\begin{array}{r|ccc} &z&=&g&( &t&)&=&t+5\\ &\uparrow&&\uparrow&&\uparrow&&&\uparrow\\ \text{name: }&\text{dependent }&&\text{function }&&\text{independent }&&&\text{independent}\\ &\text{variable }&&\text{ }&&\text{variable }&&&\text{variable} \end{array}$$
Warning: it is often acceptable (or even preferable) to omit the name of the function and concentrate on the variables, as we did in the above example.
Thus, the independent variable is the input and the dependent variable is the output. When the independent variable is specified, so is the dependent variable, via the substitution: $$\begin{array}{ccc} f&( &3&)&=&3^2\\ \uparrow&&\uparrow&&&\uparrow\\ \text{function }&&\text{input }&&&\text{output } \end{array}$$ We can think of this notation as a “black funnel”:
Here $x$ enters through the funnel and then -- after processing -- $y$ appears from the other end. We can also replace $x$ in the formula with a blank box as an entry gate: $$\begin{array}{ccc} f&( &\square &)&=&\square ^2\\ &&\uparrow&&&\uparrow\\ &&\text{ insert input }&&&\text{insert input} \end{array}$$
Example (plug in). For a more complex function, there may be several boxes, but the idea remains the same: insert the input value in all of these boxes. For example, this function: $$f\left(x \right)=\frac{2x^2-3x+7}{x^3+2x+1},$$ can be understood and evaluated via this diagram: $$f\left( \square \right)=\frac{2\square^2-3\square+7}{\square^3+2\square+1}.$$ For example, we just insert $3$ at each of these windows: $$f\left( \begin{array}{|c|}\hline\ 3 \ \\ \hline\end{array} \right)=\frac{2\begin{array}{|c|}\hline\ 3 \ \\ \hline\end{array}^2-3\begin{array}{|c|}\hline\ 3 \ \\ \hline\end{array}+7}{\begin{array}{|c|}\hline\ 3 \ \\ \hline\end{array}^3+2\begin{array}{|c|}\hline\ 3 \ \\ \hline\end{array}+1}.$$ It is as if the opening of the funnel is split and the value of $x$ is copied to several tubes that feed this value to these locations within the formula. $\square$
Warning: when substituting, use parentheses generously!
Example (substitute). If you substitute mindlessly expressions that are more complex, errors are inevitable. For example, consider the same function as above but evaluate it at $x=-2$. “Plugging in” might produce this gibberish: $$f\left(-2 \right)=\frac{2-2^2-3-2+7}{-2^3+2-2+1}.$$ One may consider a slightly different diagram: $$f \begin{array}{|c|}\hline\ (x) \ \\ \hline\end{array} =\frac{2\begin{array}{|c|}\hline\ (x) \ \\ \hline\end{array}^2-3\begin{array}{|c|}\hline\ (x) \ \\ \hline\end{array}+7}{\begin{array}{|c|}\hline\ (x) \ \\ \hline\end{array}^3+2\begin{array}{|c|}\hline\ (x) \ \\ \hline\end{array}+1}.$$ In other words, we don't substitute $x$ but $(x)$, just as the function notation suggests. Then, we have $$f\left(-2 \right)=\frac{2(-2)^2-3(-2)+7}{(-2)^3+2(-2)+1}.$$ We can have more complex substitutions: $$f\left(t+5 \right)=\frac{2(t+5)^2-3(t+5)+7}{(t+5)^3+2(t+5)+1}.$$ $\square$
Exercise. Provide a formula for the new function $f(z^2)$ made from the function $f$ above.
Example (sequence of steps). We can also take the function from the beginning of the section; it requires several stages: $$y=x+3,\quad z=y\cdot 2,\quad u=z^2,$$ can be written as: $$\square\ \to\ \square+3\ \to\ \square\cdot 2\ \to\ \square^2\ \to\quad \square . $$ We compute it for input $x=2$ consecutively: $$2\ \to\ 2+3=5\ \to\ 5\cdot 2=10\ \to\ 10^2\ \to\ 100. $$ $\square$
Example (decomposition). Consider this formula: $$f(x)=\sqrt{x^2-3}+5.$$ To represent this function as a list of instructions, we just read the formula starting with $x$: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ square } \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ subtract }3 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ take square root}\\ \hline\end{array} \mapsto & \begin{array}{|c|}\hline\text{ add }5 \\ \hline\end{array} & \mapsto & \text{output } \end{array}.$$ $\square$
Exercise. Represent this function as a list of instructions: $$f(x)=\big( \sqrt{x}+2\big)^3.$$
Example (formulas). Conversely, a diagram can be converted to a single formula. Let's take a flowchart from an example above and substitute along the arrows eliminating the intermediate variables one by one: $$\begin{array}{lll} x&\to&x+3&=&y\\ &&&&\downarrow\\ &&&&y\cdot 2&=&z\\ &&&&&&\downarrow\\ &&&&&&z^2&=&u, \end{array}\quad\begin{array}{lll} x&\to&\\ &&\\ &&(x+3)\cdot 2&=&z\\ &&&&\downarrow\\ &&&&z^2&=&u, \end{array}\quad\begin{array}{lll} x&\to&&&\\ &\\ &\\ &&&\\ &&\to&\big((x+3)\cdot 2\big)^2&=&u. \end{array}$$ In other words, our function is given by: $$u=f(x)=\big((x+3)\cdot 2\big)^2.$$ Note that to recover the operations from the formula, we just read it from inside out: $$\begin{array}{ccc} x\\ x+3\\ (x+3)\\ (x+3)\cdot 2\\ \big((x+3)\cdot 2\big)\\ \big((x+3)\cdot 2\big)^2 \end{array}$$ $\square$
Exercise. Find a formula for the following function: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ divide by }2 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ take its reciprocal } \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ subtract } 1\\ \hline\end{array} \mapsto & \text{output } \end{array}.$$
A function can also be represented by a list of pairs of inputs and outputs. This list is a table with two columns, for $x$ and $y$: $$\begin{array}{l|ll} x&y=f(x)\\ \hline 0&1\\ 1&3\\ 2&4\\ 3&0\\ 4&2\\ ...&... \end{array}$$ This is a numerical representation as the list contains only numbers. Any list like this would do as long as there are no repetitions in the $x$-column!
To create larger lists, one uses a spreadsheet. Each value in the $y$-column is computed from the corresponding value in the $x$-column via some algebraic formula:
For example, for $y=x^2$, we have in the $y$-column the following spreadsheet formula: $$\texttt{ =RC[-1]^2 } .$$ It refers to the value located in: same row, previous column.
Furthermore, it is possible that a function is pure data and there is no formula! Indeed, these may be made-up numbers such as the ones in the table above. One can also imagine that the table has come from a measuring device (say, a thermometer) that takes readings at equal intervals of time.
Even though the data in the list represents the same function as above, as we can see, there are gaps in the data. We can't tell, for example, what $1.5^2$ is or what $100^2$ is. Thus, our algebraic representation is complete, but the numerical representation given by the list is not. However, this list does represent a function, with smaller domain than the original.
The advantage of numerical representation is that it has been calculated for you so that you can see patterns; for example, with $x$ increasing we see that
- $y$ is also increasing;
- $y$ also grows faster and faster.
If the last observation is hard to see in the data, we either produce more data -- such compute the difference -- or visualize it.
We can use the list data to plot points, which leads us to the graphical representation. We just repeat the definition we had for relations.
Definition. The graph of a numerical function $y=f(x)$ is the set of points in the $xy$-plane that satisfy $y=f(x)$. In other words, it is the following set: $$\{(x,y):\ y=f(x)\}.$$
For example, we can plot the above data; just the points that have been provided:
Warning: we speak of “a graph”, or “graphs”, when we deal with the graph of some function.
Example (plotting). A spreadsheet software comes with graphic capabilities. It will plot all points you have in the list:
It can also automatically add a curve connecting these points. $\square$
Warning: the first one is the truth; the rest is a guess...
Note that when $x$ and $y$ represent two variables that have nothing to do with each other -- such as time and location -- neither do the two axes. In that case, neither the unit lengths nor the locations of the origins have to match:
A transformation takes the domain $X$, a subset of the real line, transforms it -- shift, stretch, flip, etc. -- and places the result on the codomain $Y$. It is discussed in the next chapter.
An algorithm is a verbal representation of a function. It may contain no explicit algebra. Instead, it tells us how to get a certain output given any input. For example,
- Question: How do we get from $x$ to $y$?
- Answer: Let $y$ be equal to the square of $x$.
This representation also gives us compete information about the function.
Example (diagram). Describe what this function does: $$f(x)=\dfrac{x^{2} + 1}{x^{2} -1},$$ verbally:
- Step 1: multiply $x$ by itself, call it $y$;
- Step 2: add 1 to $y$, call it $z$;
- Step 3: subtract 1 from $y$, call it $u$;
- Step 4: divide $z$ by $u$.
There is fork in the diagram: $$\begin{array}{lllll} & & & & y+1=z \\ & & & \nearrow&& \searrow \\ x & \to &x^2=y \to &&&&z/u=w \\ & & & \searrow && \nearrow \\ & & & &y-1 =u \\ \end{array}$$ $\square$
A (numerical) function is a rule or procedure $f$ that assigns to any number $x$ in a set $X$, called the set of inputs or the domain, one number $y$ in another set of real numbers $Y$, called the set of outputs or the codomain of $f$.
In other words,
- 1. each $x$ in $X$ has a counterpart in $Y$, and
- 2. there is only one such counterpart.
This rule can be violated when there are too few or too many arrows for a given $x$:
Then this is not a function. It is OK, however, to have too few or too many arrows for a given $y $!
Next, let's revisit the rule -- how to get $y$ from $x$ -- that defines a function. It must satisfy:
- there is only one $y$ for each $x$.
Let's illustrate how the rule might visibly fail for each of these four representations of $f$.
Example (algebraic). In the following, very common, way to present a formula, there are two outputs for the same input (unless $x=0$): $$y=\pm x.$$ $\square$
Example (numerical). In the following list of values, the inputs aren't ordered. It is, therefore, possible that the list might contain two rows with the same $x$-values and different $y$-values: $$\begin{array}{rlr|lll} &&x&y\\ \hline &&...&...\\ &&0&22\\ &\nearrow&...&...&\nwarrow\\ \text{same!}&&...&...&&\text{different!}\\ &\searrow&...&...&\swarrow\\ &&0&55\\ &&...&... \end{array}$$ $\square$
Example (algorithmic). In this list of commands, one is either ambiguous or it produces multiple outputs:
- Step 1: ...
- ...
- Step 50: add today's date to the output of step 49.
- ...
- Step 100: ...
$\square$
Exercise. Suggest your own examples of how formulas, lists, and algorithms can fail to give us a function.
Example (graphical). The following graph has two points -- outputs -- above $x=a$:
$\square$
For the graphical representation, all it takes is a glance.
THEOREM (Vertical Line Test). A relation is a function of $x$ if and only if every vertical line crosses the graph at one point or none.
Corollary (Horizontal Line Test). A relation is a function of $y$ if and only if every horizontal line crosses the graph at one point or none.
Example (relations). Let's apply these tests. A direct examination of the graphs of the relations from the last section produces the following results. First,
- $Ax+By=C$ is a function of $x$ unless $B=0$ and is a function of $y$ unless $A=0$.
We have a variety of straight lines:
Second,
- $x^2+y^2=k$ is not a function (of $x$ or $y$).
We have concentric circles for all $k>0$:
Third,
- $xy=k$ is a function of $x$ or $y$;
We have hyperbolas for all $k\ne 0$:
Fourth,
- $x^2-y=k$ is a function of $x$ but not of $y$.
We have shifted parabolas for all $k$:
$\square$
Exercise. Describe the graphs of the relations in the cases missing in the above example:
- $Ax+By=C$ with $B=0$ or $A=0$;
- $x^2+y^2=k$ with $k\le 0$;
- $xy=k$ with $k= 0$.
Give the function a domain...
Recall that a function $F:X\to Y$ is defined as a correspondence between two sets, its domain $X$ and its codomain $Y$.
A function, therefore, is not a function unless these three items have been specified:
- a domain $X$,
- a codomain $Y$, and
- a correspondence $F$.
Now, what if $F$ is specified but $X$ and $Y$ are not?
In our running example, we may have a collection of arrows, from a boy to a ball. We need to specify $X$ and $Y$ and in such a way that we have a function, i.e.,
- there is exactly one $y$ for each $x$.
The choices may be obvious when the function is visualized:
As you can see, Ken has no preferred ball (no arrows) and, therefore, cannot be a part of the domain $X$. Baseball isn't chosen by anyone (no arrows) and can, but doesn't have to, be excluded from the codomain $Y$.
Example (enclosure). Choosing a domain is often a matter of convenience and common sense. For example, recall the problem from the beginning of the chapter about a farmer with $100$ yards of fencing material who wants to build as large a rectangular enclosure as possible for his cattle:
As this was a word problem, it was entirely up to us to decide what quantities, variables, sets, and functions to choose for our solution. We used our common sense. Recall that the area of the enclosure was expressed in terms of its width by the formula: $$A=W(50-W).$$ Any number $W$ can be processed through this formula. However, we made the implicit choice of the domain: $$X=[0,50].$$ Why? The negative widths simply don't make sense! Meanwhile, the widths above $50$ produce negative depths. We could have also excluded $W=0$ and $W=50$ (on the same grounds), but that would have removed the end-points of the graph that we plotted:
So, we chose to concentrate on those that can be legitimate solutions to the problem at hand. In the absence of such a test, we seek another approach. $\square$
When we concentrate on numerical functions, we may have nothing but a formula. Then, we need to make some decisions about the other two attributes.
First, the codomain. The simplest choice is the set of all real numbers. Its advantage is that it is the largest possible and it applies to all functions. So, unless specified otherwise, every numerical function is: $$f:X\to {\bf R}.$$
Now, the domain.
Imagine that our function is a list of instructions (an algorithm) and it is used to create a computer program. In this case, $x$, the input, passes through a black box and out comes $y$. But if our algorithm requires the computer to divide by $x$ and we give it $x=0$ as an input, it might do exactly that and there will be trouble:
So, if we have a function and the domain isn't specified, it's an oversight.
Let's consider different ways to represent a function...
We then need to choose a set of allowable inputs for the function that we already have. Algebraically, we plug various $x$'s into the formula and see if it works.
Example (division). Let $$ f(x) = \frac{1}{x} .$$ It works for all positive and all negative numbers... but let's try $x = 0$. The function fails because $\dfrac{1}{0}$ is undefined. Since $\dfrac{1}{x}$ is defined for all $x \neq 0$, we can choose the domain to be all these numbers: $$X=\{x:\ x\ne 0\}.$$ We can present the result, if necessary, in the interval notation: $$X=\{x:\ x<0\ \texttt{ OR }\ x>0\}=( - \infty, 0 ) \cup ( 0, +\infty). $$ Now, what if we take just one of them, $$X = (0, \infty )?$$ It is also a valid choice for domain. Any set that excludes $0$ will do: $$\{...,-2,-1,1,2,...\},\ [1,2],\ (-1,0),\ ...$$ So, whatever the choice of $X$ is we have a function $f:X\to {\bf R}$. $\square$
Example (from list). If the function is given by a list of inputs and corresponding outputs, the domain can be simply the set of all entries in the first column.
Here we have a function, $f:\{0,1,2,3,4,5\}\to {\bf R}$. $\square$
Example (from graph). If the function is given by its graph and nothing else, the domain is found by following each point on the graph to the $x$-axis in this manner:
It's especially easy when the graph is made of disconnected points:
We can imagine that the blue points were suspended in the air -- as the graph -- and then dropped on the ground -- producing the domain point on the $x$-axis. Here the domain is $X=\{1,1.5,2,2.5,3,3.5\}$.
When the graph is a curve, we see it as a rope being lowered down on the $x$-axis:
$\square$
What is the advantage of one domain over another? The size. A smaller domain is a constraint on what we can do with the function and we, therefore, choose the “largest possible domain”. A more precise way to describe this choice is as a certain set.
Definition. The implied domain (or the natural domain) of a formula is the set of all inputs for which the formula makes sense.
To find it, we need to look at the formula and answer the question, what can go wrong?
Example (from formula). Let $$f(x) = \frac{x^{2} + 1}{x^{2} - 1};$$ find the implied domain. We need to ensure that the input $x$ doesn't produce a $0$ in the denominator. We have the domain presented in the set-building notation: $$X=\{x:\ x^{2} - 1\ne 0\}.$$ The problem is solved in part. The second stage could be to simplify and visualize this set. To find those $x$'s that are not in the domain, we need to solve the equation: $$x^{2} - 1 = 0.$$ It follows that $x^{2} = 1$. Thus $x = -1$ and $x = + 1$. The function is defined by all values except $\pm 1$. Then, we have simplified the representation of the implied domain: $$X=\{x:\ x\ne \pm 1\}.$$ Furthermore, in the interval notation, it is the union of these three intervals: $$X = ( \infty, -1 ) \cup (-1 , 1) \cup ( 1, \infty).$$ $\square$
So, while technically a function isn't a function without a domain, a formula carries with it its own domain!
All algebraic operations are fine: any two numbers can be added, or subtracted, or multiplied, but division has an exception. What else can go wrong? Square roots of negative numbers are undefined (because the square of two negative numbers is always positive).
Example (root). Consider $$f(x)=\sqrt{x-1}.$$ To find its domain, we need to make sure that the input of the square root isn't negative. What we don't want to have is written simply as: $$x-1< 0.$$ Solving this inequality gives us: $$x< 1.$$ If in the previous example we took the solution set of an equation and excluded it from the domain, we now do that with the solution set of this inequality. Therefore, the implied domain is: $$X=\{x:\ x\ge 1\}=[1,\infty).$$ $\square$
In summary, when we face a formula, it is implied that this is a function with the following:
- the domain is the implied domain of the formula and
- the codomain is all real numbers.
There are only a couple of “problematic” algebraic operations, for now:
- division (possibly by $0$),
- even degree roots (of possibly negative numbers).
The problem of finding the domain is solved by the following methods, respectively,
- set the denominator equal to $0$ and solve the equation,
- set the expression under the radical less than zero and solve the inequality.
In either case, we produce the solution set that is then excluded from the set of real numbers. The result is the domain. How these two problems are solved is further discussed in Chapters 3 and 4 respectively.
Exercise. Show that the appearance of a division or a square root in the formula of the function doesn't always cause the domain to lose points: $$f(x)=\frac{1}{x^2+1},\quad g(x)=\sqrt{x^2+1}.$$
Exercise. Find the implied domain of the function given by the formula: $$f(x)=\sqrt{1+x}+\sqrt{1-x}.$$
Example (from algorithm). What if the function is given by a list of instructions? For example, let's find the domain of the following function: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ multiply by }2 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ add }2 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ take the reciprocal }\\ \hline\end{array} \mapsto & \begin{array}{|c|}\hline\text{ subtract }55 \\ \hline\end{array} & \mapsto &...& \text{output } \end{array}.$$ Step 3 is the problem! Through trial and error, we can discover that input $x=-1$ causes an “explosion”: $$\begin{array}{lll} -1 & \mapsto & (-1)\cdot 2=-2 & \mapsto & (-1)+2=0 & \mapsto & \frac{1}{0}= \bigotimes & \\ \end{array}$$ Let's make sure that there are no others... The input of step 3 can't be $0$. But how do we make sure that this won't happen? First, the input of step 3 is the output of step 2. Therefore, its output can't be $0$. How do we ensure that? The input of step 2 can't be $-2$! Second, the output of step 1 can't be $-2$ and, therefore, its input can't be $-1$. This is the only number we don't allow as an input of the whole function. In other words, we trace back $z=0$ -- solving equations along the way -- to the corresponding value of $x$: $$\begin{array}{lll} x & \mapsto & x\cdot 2=y & \mapsto & y+2=z & \mapsto & \frac{1}{z}=u& \mapsto & u-55=w & \mapsto &...\\ \hline x & \mapsto & x\cdot 2=y & \mapsto & y+2=z & \mapsto & z= 0\ \bigotimes& \\ x & \mapsto & x\cdot 2=y & \mapsto & y+2=z= 0 \ \bigotimes \\ x & \mapsto & x\cdot 2=y= -2 \ \bigotimes \\ x = -1 \ \bigotimes \end{array}$$ So, the implied domain is: $$X=\{x:\ x\ne -1\}.$$ Note that the operations that come after division in step 3 won't change our decision about excluding $x=-1$ from the domain but might produce more exclusions. $\square$
Exercise. What is the next (and the last) operation is the square root? Find the implied domain of the function.
Exercise. Find the implied domain of the function: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ take the square root } \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ add }3 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ take the reciprocal }\\ \hline\end{array} \mapsto \text{output } \end{array}.$$
Exercise. Find the implied domain of the function: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ multiply by }3 \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ take the square root } \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\text{ divide by }2\\ \hline\end{array} \mapsto & \begin{array}{|c|}\hline\text{ divide by }0 \\ \hline\end{array} & \mapsto & \text{output } \end{array}.$$
The graph of a function
A function may be given to us in the form of a list, a formula, or a list of instructions. Those deal with the function one input at a time. This is why one will find it hard to discern patterns that may be hidden in the function:
Graphs provide a way to have a bird's eye view of the function.
Recall that the graph of a relation is the set of points in the $xy$-plane that satisfy the relation. In the case of a function then, the graph of a function $y=f(x)$ is the set of points in the $xy$-plane that satisfy $y=f(x)$. In other words, it is the set of all possible points on the plane in the form $(x,f(x))$: $$\text{graph of }f\ = \ \{(x,y):\ y=f(x)\}.$$
Graphs is the most visual method of representing functions.
Example (from list). Suppose we have a function represented by a list of pairs of values. We can use the list data to plot points, which leads us to its graphical representation. The list and the first graph below have been seen before. We simply treat each of the rows of the list as the two coordinates of a point on the $xy$-plane:
The domain of the function is just these five values of $x$. Furthermore, we may try to extrapolate the data to the whole interval. The first graph is data; the rest are just guesses. $\square$
Exercise. Guess the shape of the curve that these dots might represent:
Example (from formula). What if the function is given by a formula, say, $y=f(x)=x^2$? We still have to build a list! We make a table with two columns, for $x$ and $y$, and then fill it using the formula one row at a time: $$\begin{array}{l|ll} x&y=x^2\\ \hline 0&0\\ 1&1\\ 2&4\\ 3&9\\ 4&16\\ \end{array}$$ With a list ready, we then plot the point just as before (left):
Note that there are gaps in the data; we can't tell, for example, what $1.5^2$ is. The data also don't go far enough; we can't tell what $100^2$ is. Thus, our algebraic representation -- the formula -- is complete but the numerical representation given by the list is not. The graph is, therefore, also just a partial representation! We can guess what happens between the points or we can let the spreadsheet do it and automatically add a curve connecting the points (right). $\square$
Exercise. Plot the graph of the function given by the list of instructions: 1. add $3$, 2. divide by $2$, 3. square the outcome.
Example (continuum). If it is known that our function is just a snapshot of a “continuous” process, such as motion, we may have to collect more information in order to make this clear:
We, for example, look at the odometer every minute instead of every hour, or every second, etc. The infinite divisibility of the real line allows us to produce collections of points on the plane with denser and denser pattern. We imagine that at the end of this process we will have an actual curve. This is not a kind of curve that is made of marbles placed close together but a rope... $\square$
Warning: The graph of a function isn't a function; it is only a visualization of its function.
In summary, this is how graphs appear: $$\begin{array}{ccc} && & & \begin{array}{|c|}\hline\quad \text{formula} \quad \\ \hline\end{array} \\ && & && \searrow \\ && && \updownarrow &&\begin{array}{|c|}\hline\quad \text{list} \quad \\ \hline\end{array} &\longleftrightarrow&\begin{array}{|c|}\hline\quad \text{graph} \quad \\ \hline\end{array} \\ && & && \nearrow \\ && & &\begin{array}{|c|}\hline\quad \text{instructions} \quad \\ \hline\end{array} \\ \end{array}$$ The double arrows are reversible.
How can we reverse the direction of the last arrow? How can we find the list of values of the function if we only have its graph? It's feasible when the graph is small.
Example (to list). We go from point to point and find the coordinates of each. Then we put these pairs of points one under the other in a list:
The domain of the new function is automatically constructed in the first column of the list. $\square$
Exercise. Create a list pf $10$ values from this graph:
Of course, if we start with a list, plot the graph, then the list built from the graph, as above, is the original list! However, we can't hope to recover an infinitely long list nor a formula.
Warning: even though we should normally refer to it as “the graph of a function”, we may informally refer to a curve that passes the Vertical Line Test as “a graph”.
Can we ever treat a graph as a function?
Let's recall the idea of function as a black box that processes the input and produces the output: $$\begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ x & \mapsto & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y \end{array}$$ $$\begin{array}{ccc} f&( &3&)&=&3^2\\ \uparrow&&\uparrow&&&\uparrow\\ \text{function }&&\text{input }&&&\text{output} \end{array}$$ Now, suppose we have a graph and nothing else. There is a function here somewhere but where in the graph is that black box? In other words, can we find the arrows from $x$'s to $y$'s that we used to illustrate functions in the beginning of the chapter?
Suppose a graph is given to us on a piece of paper. Let's build a black box for the function, $f$, it represents. For each $x$, we need to find $y$ using nothing but the graph. How?
We just reverse the process of building the graph from a list of values. This is what we do for a single input:
For as many locations on the $x$-axis as possible, we draw a red vertical line until it crosses the graph. From that point we draw a green horizontal line until it crosses the $y$-axis. This is the totality of inputs and outputs connected by arrows:
These arrows give us a visualization our newly-built function. We can, furthermore, represent this function as a list of instructions with the output of each step becoming the input of the next step:
- 1. $x$ is an input, a number;
- 2. plot the point with that coordinate on the $x$-axis of the $xy$-plane;
- 3. draw through that point a vertical line in the $xy$-plane;
- 4. find the point of intersection of that line with the graph;
- 5. draw through that point a horizontal line in the $xy$-plane;
- 6. find the point of intersection of that line with the $y$-axis;
- 7. find the coordinate of that point;
- 8. this number, $y=f(x)$, is the output.
Just as in the last section, we can examine the list to find what can go wrong with the procedure. There are two possibilities:
- too few $y$'s for a given $x$ (none), and
- too many $y$'s for a given $x$ (two or more).
The only step that may cause trouble is #4.
First, what if there is no intersection? If there is no point in common of the vertical line -- the input of this step -- and the graph, then there is no such point -- the output of this step. As a result, the function breaks down (just as $f(x)=1/x$ breaks down if the input is $x=0$). This means that that $x$ is in not in the domain of our function! We can see this happening with the graph above for the values of $x$ that are too small or too large. So, the implied domain of this function is $$\text{ domain }= \{x:\ \text{ there is a point on the graph with its }x\text{-coordinate equal to }x\}.$$
Second, what is there are more than one such points of intersection. Then the Vertical Line Test is violated and this is simply not a function!
Exercise. Write a list of instructions of how to obtain a list of values from a graph.
Graphs, usually, have these two important features.
Definition. Suppose $y=f(x)$ is a numerical function. Then the $y$-intercept of $f$ is the number $y$ that satisfies: $f(0)=y$.
There can be only one (or none depending on the domain) of these. Finding it amounts to a simple substitution.
In other words, this is the $y$-coordinate of the point where the graph crosses the $y$-axis.
Definition. Suppose $y=f(x)$ is a numerical function. Then an $x$-intercept of $f$ is any number $x$ that satisfies: $f(x)=0$.
There may be many (or none) of these. Finding them amounts to solving this equation.
In other words, these are the $x$-coordinates of the points where the graph crosses the $x$-axis.
Exercise. Find the $x$- and $y$-intercepts for the graphs in this section.
Linear functions
The dependence of $x$ on $y$ in a numerical function can be very simple.
However, the simplest kind of function is such that its output does not change with the input! This is a constant function, i.e., it is given by a formula: $$f(x)=k\text{ for all } x,$$ for some predetermined number $k$. Its implied domain is, of course, $X=(-\infty,\infty)$. Its computation is non-existent; for example, when $k=3$, we have: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ produce }3 \\ \hline\end{array} & \mapsto & \text{output } \end{array}.$$ As you can see, the input is thrown away. This is the list of values of this function: $$\begin{array}{l|ll} x&y=f(x)\\ \hline 0&3\\ 1&3\\ 2&3\\ 3&3\\ 4&3\\ ...&... \end{array}$$ Plotting a few of these points reveal that the graph is a horizontal line:
Indeed, the relation is $y=3$.
The next simplest function is the one that does nothing to the input; i.e., it is given by a formula: $$f(x)=x.$$ Its implied domain is, of course, $X=(-\infty,\infty)$. Its computation is trivial: $$\begin{array}{ccc} \text{input} & \mapsto & \begin{array}{|c|}\hline\text{ pass it } \\ \hline\end{array} & \mapsto & \text{output } \end{array}.$$ This time, the input isn't thrown away but there was still no algebra needed. This is its list of values: $$\begin{array}{l|ll} x&y=f(x)\\ \hline 0&0\\ 1&1\\ 2&2\\ 3&3\\ 4&4\\ ...&... \end{array}$$ Plotting a few of these points reveal that the graph is the $45$ degree line:
Indeed, the relation is $y=x$.
Warning: if we say that $y$ is $x$, then the $xy$-plane should have the same units for the two axes.
Exercise. Plot the function that represents the location as it depends on time if the speed is one foot per second.
So far, no algebra! Linear polynomials are the next level of complexity...
Definition. A linear function is a numerical function given by this formula: $$f(x) = m\cdot x +b ,$$ for some predetermined numbers $m$ and $b$. When $m\ne 0$, such a function is called a linear polynomial.
So, the simplest algebra has appeared: addition/subtraction and multiplication by a constant number. They are visible in its flow-chart: $$\begin{array}{ccc} f:& x & \mapsto \begin{array}{|c|}\hline\quad \text{ multiply by }m \quad \\ \hline\end{array} & \mapsto & \begin{array}{|c|}\hline\quad \text{ add }b \quad \\ \hline\end{array} & \mapsto & y. \end{array}$$
The formula is commonly called the slope-intercept form of the linear function: $$\begin{array}{lll} f(x) = & m&\cdot &x & +&b \\ & \uparrow &&&& \uparrow \\ & \text{slope} &&&& y\text{-intercept} \end{array}$$
The latter is indeed the $y$-intercept of the function: $$f(0) = m\cdot 0 +b=b.$$
The former is understood as follows. Suppose we have two points in a specified order, say, $A$ then $B$. As we imagine moving from $A$ to $B$, the slope is defined by: $$\text{slope } =m=\frac{\text{rise}}{\text{run}}=\frac{\text{change of }y}{\text{change of }x}.$$
Exercise. Can the rise be zero? Can the run?
The geometric meaning of the numerator and denominator is seen below:
Here we have:
- run $=\ 8-2=6$, and
- rise $=\ 10-1=9$, therefore,
- slope $= \frac{9}{6}=\frac{3}{2}=1.5$.
“Rise” and “run” in this context aren't meant to substitute for “lengths of these segments” or “distances between those points”. In contrast to plain geometry, one or both of them can be negative! In particular, the slope remains unchanged if we reverse the order of the two points: $B$ first, $A$ second:
Indeed:
- run $=\ 2-8=-6$, and
- rise $=\ 1-10=-9$, therefore,
- slope $= \frac{-9}{-6}=\frac{3}{2}=1.5$.
Definition. Suppose we have two distinct points on a straight line in a specified order, say, $$A=(x_0,y_0)\ \text{ and }\ B=(x_1,y_1);$$ then the slope of the line they determine is defined by the formula: $$m=\frac{\text{change from }y_0 \text{ to } y_1}{\text{change from }x_0 \text{ to } x_1}=\frac{y_1 -y_0}{x_1 -x_0}.$$
THEOREM. The slope from $A$ to $B$ is equal to the slope from $B$ to $A$.
Proof. If we reverse the order of the two points -- $B$ first, $A$ second -- both numerator and denominator simply flip their signs: $$\text{change from }y_1 \text{ to } y_0=-(\text{change from }y_0 \text{ to } y_1)$$ and $$\text{change from }x_1 \text{ to } x_0=-(\text{change from }x_0 \text{ to } x_1).$$ But if the numerator and denominator of a fraction flip their signs, the fraction remains intact: $(-a)/(-b)=a/b$. We have for the slope: $$\frac{y_0 -y_1}{x_0 -x_1}=\frac{-(y_1-y_0)}{-(x_1 -x_0)}=\frac{y_1 -y_0}{x_1 -x_0}=m.$$ $\blacksquare$
While a positive slope appears when the rise and the sun have the same sign, a negative slope appears when the signs are opposite:
THEOREM. Any two points chosen on a straight line produce the same slope.
Exercise. Prove the theorem. Hint: similar triangles.
What does the slope tell about the linear function it represents?
Below we arrange all linear functions according to their slopes (as if the $y$-intercept is the same):
It's as if increasing the slope rotates the line counterclockwise. This diagram will be very useful even when we deal with non-linear functions.
Exercise. How far can we rotate?
Warning: comparing the line with $m=1$ and the line with $m=-2$ suggests that the word “steepness” as a substitute for slope should be used with caution.
We can assign an angle to each of these lines, of course. The approach via the slopes, however, is simpler! The slope of $m$ means that, as we follow the line, we make a step of $1$ unit to the right and then $m$ units up (it translates into a down step when $m<0$).
Warning: the slope is meaningless without axes as a frame of reference.
Exercise. What happens to the slope of a line drawn on a piece of paper for different choices of the axes?
It is also easy to observe that:
- if $m > 0$, then the outputs $y=f(x)$ are increasing as the inputs $x$ are increasing;
- if $m < 0$, then the outputs $y=f(x)$ are decreasing as the inputs $x$ are increasing;
- if $m = 0$, then the outputs $y=f(x)$ remain the same as the inputs $x$ are increasing; i.e., $f$ is a constant function.
Warning: even though straight lines remain straight lines if we resize the plot, the values of their slopes lose their geometric meaning.
Exercise. Arrange all linear polynomials with the same slope according to their $y$-intercepts.
The slope gives us the direction of the line. That's how the slope-intercept formula, $y=mx+b$, works: we start at the $y$-intercept, $(0,b)$, and the proceed in the direction provided by the slope, $m$. In the same manner, we can start at any point. Suppose a point is given, say, $A=(x_0,y_0)$. From there, we go as described above: $1$ unit right (the run) and $m$ units up (the rise).
Example (plotting). Let's plot the straight line with slope $m=2$ through the point $A=(-2,-2)$. From $A$, we make one step right and two steps up. We have a new point, say $B$, with coordinates $B=(-1,0)$.
With a ruler, we draw a line through $A$ and $B$. $\square$
Exercise. Plot the straight line with slope $m=-2$ through the point $A=(-1,-1)$. Make up your own parameters and plot the line. Repeat.
Exercise. What is the equation of the line through the points $A=(-1,2)$ and $B=(2,1)$?
Suppose, again, a point is given, $A=(x_0,y_0)$, and the slope is known to be $m$. From $A$, we go $1$ unit right and $m$ units up, repeated as many times as necessary: $$(x_0,y_0)\ \leadsto\ (x_0+1,y_0+m)\ \leadsto\ (x_0+2,y_0+2m)\ \leadsto\ (x_0+3,y_0+3m)\ \leadsto\ ...$$ We can move left too: $$(x_0,y_0)\ \leadsto\ (x_0-1,y_0-m)\ \leadsto\ (x_0-2,y_0-2m)\ \leadsto\ (x_0-3,y_0-3m)\ \leadsto\ ...$$ We have a sequence of points forming a line:
Suppose we have a specified point $(x_0,y_0)$ on our line. Let's consider an arbitrary point $X=(x,y)$ on the line.
The run is $x-x_0$ and the rise is $y-y_0$. Therefore, the slope is: $$m=\frac{y-y_0}{x-x_0}.$$ Here $x$ cannot be equal to $x_0$. Instead, we rewrite this formula in such a way that we produce a new form of a linear equation called the point-slope form.
THEOREM (Point-slope form). A line with slope $m$ passing through point $(x_0,y_0)$ is given by: $$\begin{array}{|c|}\hline\quad y-y_0 = m\cdot (x -x_0).\quad \\ \hline\end{array}$$
This equation represents a linear relation!
Exercise. What is the difference between the two relations: $$y-y_0 = m\cdot (x -x_0) \ \text{ and }\ m=\frac{y-y_0}{x-x_0}\ ?$$
Even though we can solve for $y$ any time we want, this form is often preferable over the slope-intercept form because in it the rise and the run are still visible: $$\begin{array}{ccc} \text{rise}&&\text{slope}&&\text{run}\\ (y-y_0) &= & m&\cdot &(x -x_0)& \\ \end{array}$$ The coordinates of a fixed point $A=(x_0,y_0)$ and a variable point $X=(x,y)$ on the graph are visible too: $$\begin{array}{ccc} \text{point }X&&&& &&\text{point }X\\ \downarrow&&&& &&\ \ \downarrow\ \\ y&-&y_0 &= & m&\cdot &(x& -&x_0)& \\ &&\uparrow&& &&&&\uparrow\ \\ &&\text{point }A&& &&&&\text{point }A& \end{array}$$
Exercise. Find the $y$-intercept from the point-slope form.
Example (plotting). What is the slope of the line that follows this path: we make $p$ steps right and $q$ step up as we follow the line:
Then the equation becomes: $$p(y-y_0) =q(x -x_0).$$ The slope is $m=q/p$. $\square$
Example (velocity). Furthermore, the slope is the characteristic of a linear function that tells us how fast the output is changing relative to the change of the input. An important illustration of this idea we saw early in this chapter when these were time and location respectively; then the slope is the velocity. The examples also showed how the velocity may change incrementally and cause the location to change linearly interval by interval:
In fact, we might be able to zoom in on a curve and see the same pattern... In light of Chapter 1, we see here two, very short, sequences: $$x_0,\ x_1\ \text{ and }\ y_0,\ y_1.$$ The slope is then the ratio of their differences: $$m=\frac{\text{difference of }y_n}{\text{difference of }x_n}=\frac{y_1 -y_0}{x_1 -x_0}=\frac{\Delta y}{\Delta x}.$$ This expression is called the difference quotient. It gives us the velocity when $y_n$ is location and $x_n$ is time. We face another, non-geometric, interpretation of the slope, one that will be important throughout calculus, the rate of change of the function. $\square$
Exercise. Suppose both the domain and the codomain of a linear function are the integers (as in the picture above). What can you say about the slope in this case?
Algebra creates functions
More complex algebra produces functions with more complex patterns that we will need to discover.
We introduce new algebra into functions building: multiplication of the input of the function by itself.
First, the square function: $$f(x)=x^2.$$
What is the difference between multiplication in $3\cdot x$ and in $x\cdot x$? To begin with, the former is about tripling a quantity of any nature, while the latter may be about the area of a square $x\times x$. Second, computing the latter requires -- in contrast to most previous examples of functions -- making a copy of the input first: $$\begin{array}{ccc} x & \mapsto & \begin{array}{|c|}\hline & \begin{array}{ccc} x&\mapsto &\begin{array}{|c|}\hline\quad \text{ pass it } \quad \\ \hline\end{array} \\ &&\downarrow\\ x&\mapsto &\begin{array}{|c|}\hline\quad \text{ multiply by }x \quad \\ \hline\end{array} & \mapsto&y \\ \end{array}\\ \hline \end{array} & \mapsto & y \end{array}.$$
Now the attributes of this function.
First, without division or roots, the domain is everything: $(-\infty, +\infty )$. The second observation is that the values cannot be negative.
Further, let's have a small table of values: $$\begin{array}{r|c} x&y=f(x)=x^2\\ \hline -3&9\\ -2&4\\ -1&1\\ 0&0\\ 1&1\\ 2&4\\ 3&9\\ \end{array}$$ We notice right away that the values (outputs) of $f$ first decrease, up to $x=0$, and then increase. That can't happen to a linear function!
We also notice something else that distinguishes this function from all linear functions except the constant function:
- different inputs can produce same outputs.
For example: $$(-1)^2=1^2.$$
There are many of these. In fact, a pattern starts to emerge: $$\text{different inputs }\left\{\begin{array}{c} -3\ 9\\ \left\{\begin{array}{c} -2\ 4\\ \left\{\begin{array}{c} -1\ 1\\ \ \ 0\ 0\\ \ \ 1\ 1\\ \end{array}\right\}\\ \ \ 2\ 4\\ \end{array}\right\}\\ \ \ 3\ 9\\ \end{array}\right\}\text{ same output }$$ They are paired up! There seems to be a large-scale symmetry among the values: they start to repeat themselves -- in reverse order -- after we pass $x=0$. The symmetry becomes vivid once we plot these seven points:
When we connect the points to create a curve, we see that its left branch is a mirror image of its right branch.
As an alternative to a mirror, we can fold the sheet of paper with the $xy$-plane on it in half along the $y$-axis and make one branch of the curve land on top of the other:
Exercise. Suggest examples of objects with a mirror symmetry.
This graph is a parabola.
Exercise. Repeat the above analysis for (a) $f(x)=x^2+1$, (b) $g(x)=-x^2$, (c) $h(x)=-x^2+1$.
Example (motion). Why do we connect these points in this manner? Because we try to avoid these two “undesirable” features in the graph:
- gaps and breaks,
- corners and cusps.
If we are to model motion, our function might represent the location as a function of time. Then these two features are to be avoided because they represent certain implausible events:
- the former would represent an abrupt or even instant change of position and
- the latter a sudden or even instant change of velocity or direction.
It is, however, not unusual for man-made functions to change incrementally. The two issues are addressed in Chapters 5 and 6 respectively. $\square$
Another thing we notice that distinguishes this function from linear functions is the slope. It is, in fact, “slopes”; they are different at different locations!
Indeed,
- the slope from $(0,0)$ to $(1,1)$ is $\frac{1-0}{1-0}=1$, but
- the slope from $(1,1)$ to $(2,4)$ is $\frac{4-1}{2-1}=3.$
There is no single straight line on the graph!
Exercise. What pattern do the slopes exhibit?
With these observation having been made, we know what to look for in every function to come up.
Second, the cubic function: $$f(x)=x^3.$$
While the square function above may be about the area of a square $x\times x$, the this one may be about the volume of a cube $x\times x\times x$.
The domain is everything: $(-\infty ,+\infty )$, again. In contrast, the values can be negative: $$\begin{array}{r|c} x&y=f(x)=x^2\\ \hline -3&-27\\ -2&-8\\ -1&-1\\ 0&0\\ 1&1\\ 2&8\\ 3&27\\ \end{array}$$ We notice right away that the values (outputs) of $f$ increase throughout! That's different from the square function.
We also notice something else that distinguishes this function from the last: different inputs don't produce same outputs ($(-1)^3\ne 1^3$) but there is another pattern: $$\text{different inputs }\left\{\begin{array}{c} -3\ -27\\ \left\{\begin{array}{c} -2\ -8\\ \left\{\begin{array}{c} -1\ -1\\ \ \ 0\quad 0\\ \ \ 1\quad 1\\ \end{array}\right\}\\ \ \ 2\quad 8\\ \end{array}\right\}\\ \ \ 3\quad 27\\ \end{array}\right\}\text{ same output but with opposite sign}$$ They are paired up as before but differently. There seems to be a large-scale symmetry among the values: they start to repeat themselves -- in reverse order with opposite signs -- after we pass $x=0$. The symmetry becomes vivid once we plot these seven points:
In contrast, the left branch is not a mirror image of its right branch! It there another symmetry? Yes, it is called the central symmetry:
The idea of this transformation can be traced back to the “camera obscura”:
There are many objects with this symmetry; for example, some double-edge swords have it and some don't:
Exercise. Suggest examples of other objects with a central symmetry.
Exercise. Repeat the above analysis for (a) $f(x)=x^3+1$, (b) $g(x)=-x^3$, (c) $h(x)=-x^3+1$.
Once again, the slopes are different in different locations!
Indeed,
- the slope from $(0,0)$ to $(1,1)$ is $\frac{1-0}{1-0}=1$, but
- the slope from $(1,1)$ to $(2,8)$ is $\frac{8-1}{2-1}=7.$
Exercise. What pattern do the slopes exhibit?
Warning: in contrast to a geometric progression, the multiplication in a power function is repeated a fixed number of times.
As building blocks for future, more complex functions (Chapter 4), we introduce a whole sequence of (positive) power functions: $$ \underbrace{x^{0} = 1}_{\text{constant}},\ \underbrace{x}_{\text{linear}},\ \underbrace{x^{2}}_{\text{quadratic}},\ \underbrace{x^{3}}_{\text{cubic}},\ ...\ ,\ \underbrace{x^{n}}_{n\text{th degree}},\ ... $$ Beyond the first few, we use the power of $x$, called the degree, to identify these functions. But first, let's see how they are computed: $$\begin{array}{ccc} x^4:& x & \mapsto & \begin{array}{|c|}\hline &\begin{array}{ccc} x&\mapsto &\begin{array}{|c|}\hline\quad \text{ pass it } \quad \\ \hline\end{array} \\ &&\downarrow\\ x&\mapsto &\begin{array}{|c|}\hline\quad \text{ multiply by }x \quad \\ \hline\end{array} \\&&\downarrow\\ x&\mapsto &\begin{array}{|c|}\hline\quad \text{ multiply by }x \quad \\ \hline\end{array} \\&&\downarrow\\ x&\mapsto &\begin{array}{|c|}\hline\quad \text{ multiply by }x \quad \\ \hline\end{array} & \mapsto&y \\ \end{array}\\ \hline \end{array} & \mapsto & y \end{array}.$$
The same questions are asked and answered about these new functions: the domains are all real numbers, etc.
The magnitude of the degree affects the shape of the graph:
The higher the degree, the slower the graph grows from $x=0$ and the faster it rises from $x=1$. They all meet at $(0,0)$ and $(1,1)$.
We can see a pattern below:
One might be tempted to say that all the graphs in the first row -- these are the even powers -- “look like” parabolas.
Warning: the graph of $y=x^4$ is not a parabola.
We recognize that $x^4,\ x^4,\ ...$ have flatter bottoms (relative to the growth that follows). When the power is odd, the graphs “look like” that of $x^3$ but flatter around $0$. Thus, the parity of degree, i.e., even vs. odd, significantly affects the shape of the graph:
- the graphs of the even degree powers have mirror symmetry about the $y$-axis, while
- the graphs of the odd degree powers have central symmetry about the origin.
Understandably, functions with the former kind of symmetry are called “even” and the latter “odd”. These functions are discussed in Chapter 4.
Also,
- the outputs of the even degree powers go down and then up, while
- the outputs of the odd degree powers go only up.
Exercise. Sketch what you think $y=x^5$ and $y=x^6$ look like.
No division until now!
Next, the reciprocal function: $$f(x)=\frac{1}{x}.$$ We see the difference right away. We can't divide by $0$ and, therefore, the domain is: $$\{x:\ x\ne 0\}=(-\infty,0)\cup(0,+\infty).$$ Because of the hole in the domain, the graph consists of two branches.
A few values: $$\begin{array}{r|c} x&y=f(x)=1/x \\ \hline -3&-1/3\\ -2&-1/2\\ -1&-1\\ \hline \hline 1&1\\ 2&1/2\\ 3&1/3\\ \hline \end{array}$$ We notice right away that the values (outputs) of $f$ decrease throughout either of the two halves of the domain!
Just as with $x^3$, different inputs cannot produce same outputs but there is another pattern: $$\text{different inputs }\left\{\begin{array}{c} -3\ -1/3\\ \left\{\begin{array}{c} -2\ -1/2\\ \left\{\begin{array}{c} -1\ -1\\ \ \ \quad \\ \ \ \ 1\quad 1\\ \end{array}\right\}\\ \ \ \ 2\quad 1/2\\ \end{array}\right\}\\ \ \ \ 3\quad 1/3\\ \end{array}\right\}\text{ outputs with opposite signs}$$ The symmetry is visible in the graph:
However, the pattern of behavior to the right and to the left of these points isn't entirely clear yet. Adding a couple at either end shows that the graph starts to approach the $x$-axis, seems to almost merge with it but never actually reach it:
We say that $y=0$ (the $x$-axis) is a “horizontal asymptote” of the graph.
But what is going on closer to the hole in the domain, $0$? Let's insert points in the middle: $$\begin{array}{l|ccc} x&-3&-2&-1&-1/2&-1/3&-1/4&-1/5&\circ &1/5&1/4&1/3&1/2&1&2&3\\ \hline y=1/x&-1/3&-1/2&-1&-2&-3&-4&-5&&5&4&3&2&1&1/2&1/3 \end{array}$$ The result shows that the graph starts to approach the $y$-axis, seems to almost merge with it but never actually reach it:
We say that $x=0$ (the $y$-axis) is a “vertical asymptote” of the graph. This curve is a hyperbola.
Relying on a computer to “connects the dots” might cause errors:
Again, the symmetry is a central symmetry (also a rotation $180$ degrees around the origin):
Exercise. The graph has also a mirror symmetry; point it out.
Exercise. Take another look at the last exercise.
As there are more and more functions, we can't devote as much time and attention to each and every one of them. Often, we will get only a bird's eye view of classes of functions...
In light of Chapter 1, in addition to the positive power functions, we now have the negative power functions, as the reciprocals of the power functions: $$x^{-1}=\frac{1}{x^1},\ x^{-2}=\frac{1}{x^2},\ x^{-3}=\frac{1}{x^3},\ ....,\ x^{-n}=\frac{1}{x^n},... $$ They are easy to compute if we have the former functions available. For example, this is how one computes $1/x^3$: $$\begin{array}{ccc} x&\mapsto &\begin{array}{|c|}\hline\quad \text{cube it} \quad \\ \hline\end{array}&\mapsto &\begin{array}{|c|}\hline\quad \text{ take its reciprocal} \quad \\ \hline\end{array} & \mapsto&y. \end{array}$$
The main difference from the positive powers is in the domains as $0$ must be excluded. The domains of all of these functions are the same: $$\{x:\ x\ne 0\}=(-\infty,0)\cup(0,+\infty).$$
Instead of just recognizing patterns in a behavior of a single function, we try to see them in a whole group of functions. For example, the magnitude of the degree affects the shape of the graph:
The higher the degree, the faster the graph drops from $x=0$ and the slower it declines from $x=1$. They all meet at $(1,1)$.
We recognize that as we move along the sequence of functions $1/x^3,\ 1/x^4,\ ...$, the graphs are getting flatter and flatter: almost vertical or almost horizontal! When the power is odd, the graphs “look like” that of $1/x$ but closer to the $x$- and $y$-axes. Once again, the parity of degree significantly affects the shape of the graph:
- the graphs of the even degree powers have mirror symmetry about the $y$-axis, while
- the graphs of the odd degree powers have central symmetry about the origin.
Also,
- the outputs of the even degree powers go up and then down, while
- the outputs of the odd degree powers go only down, within either of the two halves of the domain.
Warning: we can't simply say that the values of an odd degree negative power function decrease, not across the hole in the domain.
Exercise. Sketch what you think $y=1/x^5$ and $y=1/x^6$ look like.
These properties and features of functions are so important that we will continue to look for them in every function that comes up. Conversely, the simple functions presented in this section are the go-to examples of the features we have discovered.
The arithmetic operations on functions
At the next level, we will study functions as a group.
We will find inspiration in who we have handled the real numbers recently. We put them together in the real number line, which provides us with a bird's-eye view of them all:
We also recognize that these entities are interacting with each other producing offspring via arithmetic: $$3+6=9,\ 5\cdot 7=35, \text{ etc.}$$ Understanding this activity requires understanding that the beginning and the end of such a computation are just two different representations of the same number: $$1+1\ =\ 2\cdot 1\ =\ 2.$$ There is a single location for all these expressions on the real number line!
It is much more challenging to give such a bird's-eye view for functions! For example, this is what a visualization of all linear functions might look like:
For each of the four arithmetic operations on numbers -- addition, subtraction, multiplication, and division -- there is an operation on (numerical) functions.
But first we need to a clear understanding of what it means for two functions to be the same. For example, are these the same: $$x+x\ \text{ and }\ 2x?$$ Of course! But what about these: $$\frac{2x^2+2x}{2}\ \text{ and }\ x^2+x,$$ or those: $$\frac{2x^2+2x}{x}\ \text{ and }\ 2x+2?$$ To find out, we can just test the formulas by plugging input values and watching the outputs. In the former case, the results will be the same but in the latter plugging in $x=0$ will produce division by $0$ for the first function in the pair but not for the second. It is clear then that two functions can't be the same unless their domains are equal too (as sets).
Definition. Two functions $f$ and $g$ are called equal, or the same, if they have the same domain and $$f(x)=g(x)\quad \text{ for every }x\text{ in the domain;}$$ we also say that this is the same function.
These are our answers to the above questions. Are these two functions the same: $$f(x)=\frac{2x^2+2x}{2}\ \text{ and }\ g(x)=x^2+x?$$ Yes, because $$\frac{2x^2+2x}{2}=x^2+x \ \text{ for all every } x.$$ It is crucial that the implied domains -- for all every $x$ -- of the two functions are the same.
We then use the simple notation: $$f=g.$$
Are these two functions the same: $$f(x)=\frac{2x^2+2x}{x}\ \text{ and }\ g(x)=2x+2?$$ No, because the implied domain of the former doesn't include $0$ while that of the latter does. Even though the difference is in a single value!
We then use the simple notation: $$f\ne g.$$
As you can see, once we discover that the domains don't match, we are done. However, choosing another domain will fix the problem: $$f(x)=\frac{2x^2+2x}{x}\ \text{ and }\ g(x)=2x+2 \ \text{ are the same function on the domain } x\ne 0.$$ As another relevant example, these are two different functions:
- $x^2$ with domain $(-\infty, \infty)$;
- $x^2$ with domain $[0, \infty)$.
Exercise. Consider: $$\frac{x}{x^2}\ \text{ vs. }\ \frac{1}{x}.$$
Exercise. Suggest your own examples of functions that differ by a single value.
A statement presented in the definition, such as $$\frac{2x^2+2x}{2}=x^2+x \ \text{ for every real } x,$$ is called an identity. The last part is often assumed and omitted from computations. The following statement is also an identity: $$\frac{2x^2+2x}{x} =2x+2\ \text{ for every real } x\ne 0.$$ However, the last part serves as the caveat and cannot be omitted! In other words, an identity is just a statement about two functions being “identically” equal, i.e., indistinguishable, within the specified domain.
This idea of transitioning from a function to its twin is the basis of algebraic manipulations -- informally called “simplifications” or “cancellations” -- we are often use.
Now, the outputs of numerical functions are numbers. Therefore, any arithmetic operation -- addition, subtraction, multiplication, and division -- on numbers can now be applied to functions, one input at a time.
The definitions of these new functions are simple.
Definition. Given two functions $f$ and $g$, the sum $f+g$ of $f$ and $g$ is a function defined by: $$(f+g)(x)=f(x)+g(x),$$ for all $x$ in both of the domains of $f$ and $g$ .
Note how the two plus signs in the formula are different: the first one is a part of the name of the new function while the second is the actual sign of summation of two real numbers. This is the “deconstruction” of the notation: $$\begin{array}{lll} &&\text{names of the first and second functions}\\ &&\downarrow\qquad\quad\downarrow\\ \big(\ f+g\ \big)\ (x)&=&f(x)+ g\ (x)\quad\ .\\ \qquad\uparrow&&\quad\uparrow\quad\uparrow\quad\uparrow\\ \text{name of the new function}&&\text{operation on numbers} \end{array}$$ Furthermore, we have now an operation on functions: $f+g$ is a new function.
Example. The sum of $$g(x)=x^2\ \text{ and }\ f(x)=x+2$$ is $$(g+ f)(x)=g(x)+f(x)=\big( x^2 \big) +\big( x+2 \big).$$ Whether this is to be simplified or not, a new function has been built. $\square$
This is an illustration of the meaning of the sum of two functions:
One can see how the values are added location by location.
We represent a function $f$ diagrammatically as a black box that processes the input and produces the output: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ x & \mapsto & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y \end{array} $$ Now, what if we have another function $g$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccc} \text{input} & & \text{function} & & \text{output} \\ t & \mapsto & \begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \mapsto & u \end{array} $$ How do we represent their sum $f+g$? To represent it as a single function, we need to “wire” their diagrams together side by side: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccc} x & \mapsto & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y& \\ ||&&&&\updownarrow\\ t & \mapsto & \begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \mapsto & u \end{array}$$ But it's only possible when the input of $f$ coincides with the input of $g$. We may have to rename the variable of $g$. We replace $t$ with $x$. For the outputs, only when units are involved, we must make sure that they match so that we can add them. Then we have a diagram of a new function: $$\begin{array}{ccc} f+g:& x & \mapsto & \begin{array}{|c|}\hline &x& \begin{array}{lllll} \nearrow &x &\mapsto &\begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y & \searrow\\ \\ \searrow &x &\mapsto &\begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \mapsto & u & \nearrow\\ \end{array}& \begin{array}{|c|}\hline\text{ add } \\ \hline\end{array}\mapsto & z\\ \hline\end{array} & \mapsto & z \end{array}$$ We see how the input variable $x$ is copied into the two functions, processed by them in parallel, and finally the two outputs are added together to produce a single output. The result can be seen as just another black box: $$ \begin{array}{ccc} & x & \mapsto & \begin{array}{|c|}\hline \quad f+g \quad \\ \hline\end{array} & \mapsto & y \end{array}$$
With all of the algebraic operations, we sometimes want to “reverse” them. By doing so, we decompose the given function into two (or more) simpler parts that can then be studied separately.
Example. Represent $z = h(x) = x^{2} + \sqrt[3]{x}$ as the sum of two functions: $$ x \mapsto y=x^{2}\ \text{ and }\ x \mapsto y=\sqrt[3]{x} . $$ $\square$
Subtraction also gives us an operation on functions.
Definition. Given two functions $f$ and $g$, the difference $g-f$ of $f$ and $g$ is a function defined by: $$(g-f)(x)=g(x)-f(x),$$ for all $x$ in both of the domains of $f$ and $g$ (i.e., in their intersection).
Before we get to multiplication of functions, there a simpler but very important version of this operation.
Definition. Given a function $f$, the constant multiple $cf$ of $f$, for some real number $c$, is a function defined by: $$(cf)(x)=cf(x),$$ for all $x$ in the domain of $f$.
In the following illustration of the meaning of a constant multiple of a function one can see how its values are multiplied by $1.3$ one location at a time:
There may be more than two functions involved in these operations or they can be combined.
Example. Sum combined with differences: $$h(x)=2x^3-\frac{5}{x} +3x-4.$$ The function is also seen as the sum of constant multiples, called a “linear combination”: $$h(x)=2\cdot\left( x^3 \right)+(-5)\cdot\frac{1}{x} +3\cdot x+(-4)\cdot 1.$$ $\square$
Example. When the two functions are represented by their tables of values, the sum etc. can be easily computed. It is simple as we simply go row by row adding the values.
Suppose we need to add these two functions: $$\begin{array}{c|cc} x&y=f(x)\\ \hline 0&1\\ 1&2\\ 2&3\\ 3&0\\ 4&1 \end{array}\quad + \quad \begin{array}{c|cc} x&y=g(x)\\ \hline 0&5\\ 1&-1\\ 2&2\\ 3&3\\ 4&0 \end{array}\quad=\quad?$$ We simply add the output of the two functions for the same input. First row: $$f:0\mapsto 1\quad g:0\mapsto 5\quad \Longrightarrow\ h:0\mapsto 1+5=6.$$ Second row: $$f:1\mapsto 2\quad g:1\mapsto -1\quad \Longrightarrow\ h:1\mapsto 2+(-1)=1.$$ And so on. This is the whole solution: $$\begin{array}{c|cc} x&y=f(x)\\ \hline 0&1\\ 1&2\\ 2&3\\ 3&0\\ 4&1 \end{array}\quad + \quad \begin{array}{c|cc} x&y=g(x)\\ \hline 0&5\\ 1&-1\\ 2&2\\ 3&3\\ 4&0 \end{array}\quad =\quad \begin{array}{c|l} x&y=f(x)+g(x)\\ \hline 0&1+5=6\\ 1&2+(-1)=1\\ 2&3+2=5\\ 3&0+3=3\\ 4&1+0=1 \end{array}$$
$\square$
Example. This how the sum of two functions is computed with a spreadsheet:
The formula is very simple: $$\texttt{=RC[-6]+RC[-3]}.$$ $\square$
There are two more operations, multiplication and division.
Definition. Given two functions $f$ and $g$, the product $f\cdot g$ of $f$ and $g$ is a function defined by: $$(f\cdot g)(x)=f(x)\cdot g(x),$$ for all $x$ in both of the domains of $f$ and $g$ (i.e., in their intersection).
For each value of $x$, we use the pair $f(x)$ and $g(x)$ the sides of a rectangle. Then the product $f(x)\cdot g(x)$ is seen as the area of this rectangle:
If we think of $x$ as time, we can see the function is a short clip:
Definition. Given two functions $f$ and $g$, the quotient $f/ g$ of $f$ and $g$ is a function defined by: $$(f/ g)(x)=f(x)/g(x),$$ for all $x$ in both of the domains of $f$ and $g$ and for $g(x)\ne 0$ (i.e., in the intersection of these three sets).
For each value of $x$, we use the pair $f(x)$ and $g(x)$ as the sides of a right triangle. They are horizontal and vertical, respectively, the run and the rise. Then the quotient $f(x)/g(x)$ is the slope of this line:
Note: the implied domains of these new functions are to be determined.
Exercise. Explain the difference between these two functions: $$\sqrt{\frac{x-1}{x+1}}\ \text{ and }\ \frac{\sqrt{x-1}}{\sqrt{x+1}}.$$
All four algebraic operations produce new functions in the same manner: $$\begin{array}{ccc} x & \mapsto & \begin{array}{|c|}\hline &x& \begin{array}{lllll} \nearrow &x &\mapsto &\begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \mapsto & y & \searrow\\ \\ \searrow &x &\mapsto &\begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \mapsto & u & \nearrow\\ \end{array}& \begin{array}{|c|}\hline\quad +\ -\ \cdot\ \div \quad \\ \hline\end{array} \mapsto & z \\ \hline \end{array} & \mapsto & z \end{array}$$
Compositions are the most important operations on functions (Chapter 3).
The image: the range of values of a function
Let's go back to the set $X$ of boys, the set of balls $Y$, and the “I prefer” function $F$ from $X$ to $Y$. A simple question we may ask about it is, what do they like as a group? It has a simple answer, a list: basketball, tennis, and football. We just have to look at the arrow and record those elements of $Y$ that have an arrow arriving at it. This set, $$V=\{ \text{ basketball, tennis, football }\}\subset Y,$$ is a subset of the codomain $Y$ and represents all possible values of $F$.
In other words, this is the range of values of the function. It can be, but is not in this case, the whole codomain.
Definition. The image, or the range, of a function $F:X\to Y$ is the set of all of its values, i.e., $$\{y:\ F(x)=y \text{ for some }x\}.$$
Note that if we keep the values but change the original codomain of $F$ to its range $V$, we have a new, and different, function $G:X\to V$.
Now numerical functions... You get an idea about the range by simply looking at the $y$-column of the tables of values of the function (just as looking at the $x$-column gives you an idea about the domain). However, finding the set explicitly requires some algebra.
Linear polynomials are easy: $$y=mx+b \ \Longrightarrow\ x=\frac{y-b}{m},$$ for $m\ne 0$. So, there is an $x$ for every $y$. We have proven the following.
THEOREM. The range of a linear polynomial $y=mx+b$ is the set of real numbers, $V={\bf R}$, unless the slope is zero, $m=0$ (constant); in that case, the range is a single point, $V=\{b\}$.
Example. Can we make the same argument for $f(x)=x^2$? Of course not: squares can't be negative! What about the rest of $y$'s? $$y\ge 0 \ \Longrightarrow\ y=\left(\sqrt{y}\right)^2.$$ Therefore, the range of $x^2$ is $$\{y:\ y\ge 0\}=[0,+\infty).$$ What about $x^3$? It works for any $y$: $$y=\left(\sqrt[3]{y}\right)^3.$$ Why such a difference? In addition to the algebra above, we will appreciate the difference between the two functions by examining their graphs, especially if we thicken them and shrink the $xy$-plane:
So, the “spread” of the graph vertically gives us the range (the “spread” of the graph horizontally gives us the domain). This is how the range of $y=x^2$ is seen as a ray in the $y$-axis:
$\square$
Generally, to find the range of a numerical function the graph of which is supplied, we draw a horizontal line through every point on the graph and note where it crosses the $y$-axis. Conversely, we try to find a counterpart for each $y$ going backwards:
Example. The example of $y=1/x$ is a bit more complex. What $y$ can come from this formula? To answer, find $x$: $$y=1/x\ \Longrightarrow\ x=1/y \ \Longrightarrow\ y\ne 0.$$ In other words, the equation $1/x=0$ has no solution. We come to the same conclusion be examining the graph and discovering that it cannot touch the $x$-axis:
Therefore, the range is $$\{y:\ y\ne 0\}=(-\infty,0)\cup (0,+\infty).$$ The solution and the range are exactly the same for the rest of the reciprocals of powers... $\square$
So, these graphs cannot touch or cross the $x$-axis and that is the same as to say that $0$ isn't in the range. In the meantime, their graphs cannot touch or cross the $y$-axis and that is the same as to say that $0$ isn't in the domain. That's the analogy -- and the symmetry -- of the problems of the domain and the range (not codomain). It is the symmetry of the $x$- and the $y$-axes in the $xy$-plane.
Any set (in the $y$-axis) can be the range of some function. For example, this function's range is a bounded interval:
Definition. If the range of a function is bounded, the function is called bounded, otherwise unbounded.
The linear polynomials are unbounded (except for the constant ones) and so are all quadratic polynomials. These are some ways a function can exhibit unbounded behavior:
If the domain and the range are intervals, the graph of the function is contained in the rectangle with these sides:
Example. It is often the case that the domain is an interval and the codomain is typically chosen to be $Y={\bf R}$. So is the range:
However, the range may skip values when there are breaks in the graph:
This issue is discussed in Chapter 5. $\square$
Another question we can ask about boys and balls is, who likes basketball? or baseball, etc.? We just look at the arrow, or arrows, that arrives to this ball and note where it comes from. The result is a subset of $X$.
Definition. The preimage of an element $b$ in a set $Y$ under a function $F:X\to Y$ is the set of all $x$ the value of which is $b$, i.e., $$\{x:\ F(x)=b\}.$$
In other words, we are solving equations again.
If we carry out this computation for every ball and discover that the preimage of baseball is the empty set. This is always the case with outputs outside the range!
The picture below illustrates how to find the preimage of a point of a numerical function.
Some answers we already know:
- the preimages under a constant function are empty with an exception of a single value the preimage of which is the whole $x$-axis;
- the preimages under linear (non-constant) polynomials are single points;
- the preimages under even powers are two-point sets for positive $y$'s, a single point for $y=0$, and empty for negative $y$'s;
- the preimages under odd powers are single points.
Exercise. Prove the above statements.
Exercise. What are the preimages of the reciprocals of the powers?
Exercise. The segments of straight lines below are graphs of three functions. Find the domains and the ranges of these functions: