Forms in Euclidean spaces

Continuous and discrete forms

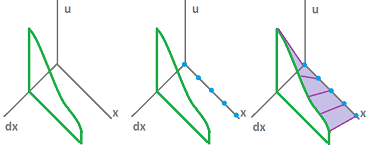
The simplest example of a differential form is a $1$-form over the real line: $$\varphi=f(x) \cdot dx,$$ where $f$ is a function of $x\in {\bf R}$ multiplied by the second variable called $dx\in {\bf R}$.

Let's plot its graph:

• first we plot the curve (green) which is the restriction of our function $\varphi$ to a fixed value of $dx$;
• then we observe that $\varphi$ is $0$ if $dx=0$ and plot those points on the $x$ -axis (blue);
• finally we connect these dots to the curve with straight lines (purple).

The construction we took from calculus also follows our definition of a continuous differential form for ${\bf R}$ over $R={\bf R}$ as a collection $\varphi$ of linear maps: $$\varphi_A:T_A({\bf R}) \to R,\ A\in {\bf R},$$ because $T_A({\bf R})={\bf R}$. The ring of coefficients $R$ can be arbitrary.

Exercise. Provide an illustration for the graph of a $1$-form in ${\bf R}^2$.

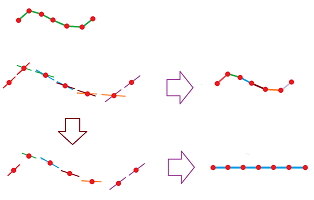
Now, let's consider its discrete counterpart. A discrete $1$-form for the real line is, by definition, a collection $\phi$ of linear maps on tangent spaces: $$\phi_A:T_A({\mathbb R})\to R,\ A\in {\bf Z}={\mathbb R}^{(0)},$$ where $R$ is an arbitrary ring of coefficients. Consider its value for $$\phi(A,AB)=\phi_A(AB),$$ where $A\in {\bf Z}$ and $B=A-1$ or $A+1$.

In order to simplify things, we utilize what we know about the algebra of directions on ${\bf R}$: the direction from $n$ to $n+1$ is the opposite to the direction from $n$ to $n-1$, written as follows: $$(n,[n,n+1]) \sim -(n,[n,n-1]).$$ Furthermore, we glue the tangent spaces together to form the bundle: the direction from $n$ to $n+1$ is the opposite to the direction from $n+1$ to $n$, written as follows: $$(n,[n,n+1]) \sim -(n+1,[n+1,n]).$$ The construction is illustrated below with the output at the lower right:

It is a straight segment. We can compare the output of the construction we used previously, i.e., only the second equivalence relation is applied. It is a topological curve.

The two relations put together show that this is the same variable, which gives us one of the two directions at any location $n$. Let's call this variable $dx$. Since the form is linear with respect to this variable, we have, again, $$\phi=f(n) \cdot dx.$$

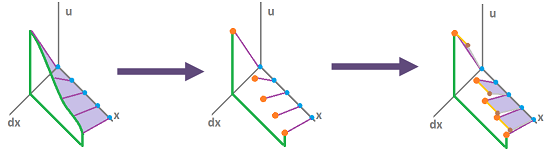
The relation between the two forms for $n=k=1$ is clear. The discrete form is simply the restriction of the continuous form to the set of integers, for the first argument: $$\phi(n,dx):=\varphi(n,dx),\ n\in {\bf Z}.$$ This operation may be called sampling.

Conversely, a discrete $1$-form can be extended to each of the $1$-cells, resulting in a continuous $1$-form.

Note that an illustration of forms over such rings as ${\bf Z}, {\bf Z}_p$ would be the same but with the straight lines dashed.

Recall that the space of continuous $k$-forms is denoted by $\Omega^k({\bf R}^n)$ and the space of discrete forms is $T^k({\mathbb R}^n)$.

Exercise. Prove that the restriction and extension described above define linear maps between $\Omega^1$ and $T^1$.

In this sense, we have $$T^1({\mathbb R}) \subset \Omega^1({\bf R}).$$

The above argument applies to show that in $3$-space the direction variables are independent from the location variables $x$, $y$, and $z$. We call them $dx$, $dy$, and $dz$. They are elements of $R$. Thus, all $1$-forms, continuous on ${\bf R}^3$ or discrete on ${\mathbb R}^3$, can be represented as: $$\varphi = f dx + g dy + h dz,$$ where $f,g,h$ are functions of $(x,y,z)$. The only difference is that in the former case, we have: $$(x,y,z)\in {\bf R}^3,$$ while in the latter case, we have $$(x,y,z)\in {\bf Z}^3.$$ Both approaches rely on the algebra of the Euclidean space.

Let's summarize the picture for ${\bf R}^3$ and ${\bf R}^2$. In these spaces, forms are made up of functions of $x$, $y$, $z$, as well as $dx$, $dy$, and $dz$ appearing linearly, as follows: $$\begin{array}{c|c|cc} \deg \varphi & {\bf R}^2,{\mathbb R}^2 & {\bf R}^3,{\mathbb R}^3\\ \hline 0 &f & f\\ 1 & f dx + g dy & f dx + g dy + h dz \\ 2 & f dx \hspace{1pt} dy & f dx \hspace{1pt} dy + g dy \hspace{1pt} dz + h dz \hspace{1pt} dx\\ 3& 0 & f dx \hspace{1pt} dy \hspace{1pt} dz\\ 4& 0 & 0 \end{array}$$ The zeros come from the fact that $$\Lambda^3({\bf R}^2)=\Lambda^4({\bf R}^3)=0.$$

Such a representation can be seen as the dot product of

• the vector of functions of the location variables and
• the vector of the direction variables.

For example, $$\varphi=< (f,g,h) , (dx,dy,dz) > = fdx + gdy + hdz.$$ Following this idea we can write for dimension $n$: $$\varphi=< V, dX >,$$ where

• $V$ is a vector function of $(x^1,x^2,...,x^n)$ (i.e., a vector field) and
• $dX=(dx^1,dx^2,...,dx^n)$.

Exercise. Find a dot product representation for $2$-forms.

Exercise. Devise a sampling procedure to show that $$T^k({\mathbb R}^n) \subset \Omega^k({\bf R}^n),\ n=2,3.$$

Exercise. Show that the function $d:f\mapsto fdx$ defines linear maps on spaces of forms.

Euclidean cell complexes

Previously, we defined the tangent spaces and the tangent bundle of the Euclidean space ${\bf R}^n$ and well as its cubical counterpart ${\mathbb R}^n$. We now consider other cell representations of ${\bf R}^n$. In addition, calculus would be incomplete unless we are able to limit it to an open subset $U$ of ${\bf R}^n$.

For ${\bf R}^n$, such a generalization is easy since any $A\in U$ has a neighborhood isomorphic to ${\bf R}^n$. What about ${\mathbb R}^n$?

The idea is as follows. Suppose cell complex $K$ is realized in ${\bf R}^n$. Then the tangent space $T_A(K)$ at vertex $A$ consists, as before, of the edges adjacent to $A$, i.e., the $1$-star $St(A)$. However, this time the algebra of $T_A(K)$ doesn't come from the $R$-module $C_1(K)$ of $1$-chains but from the algebra of ${\bf R}^n$.

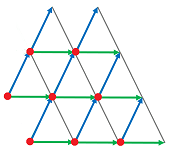
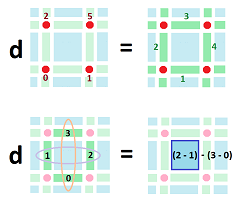
Let's review. The complex ${\mathbb R}^n$ comes with a standard orientation of all edges -- along the coordinate axes of ${\bf R}^n$. We use an algebraic relation between the edges that start at each vertex as the opposite directions are represented by two different edges. As shown below, in ${\mathbb R}^2$ we have $[k,k+1]\times \{m\}=-[k,k-1]\times \{m\}$, etc.

Then, for each vertex $A$ in ${\mathbb R}^n$, the tangent space at $A$ is the span in $C_1({\mathbb R}^n)$ of the set of the edges that originate from $A$ and are aligned with the coordinate axes of ${\bf R}^n$: $$T_A({\mathbb R}^n):=< \{AB \in {\mathbb R}^n: A \le B\} > \subset C_1({\mathbb R}^n).$$ There are $n$ of them and we have $$T_A({\mathbb R}^n) \cong R^n.$$

Thus, we allow infinite cell complexes! However, below we assume that all complexes are locally finite: each vertex has only finite number of adjacent edges.

Exercise. Show that “locally finite” implies that each edge has only a finite number of adjacent faces, etc.

Proposition. The boundary operator one a locally finite complex is well defined and satisfies the double boundary identity: $$\partial\partial =0.$$

Exercise. Prove the proposition. Hint: chains are finite.

Now, let's consider various representations of the Euclidean space as a realization of a locally finite cell complex.

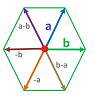
Example. Suppose ${\bf R}^2$ is represented as a realization of the cell complex of the regular triangular grid. What algebra does its tangent spaces inherit?

There are six edges per vertex:

However, it suffices to choose just two and the rest are their linear combinations: $$T_A(K) :=<a,b> \cong R^2,$$ whether $R={\bf R}$ or $R={\bf Z}$.

$\square$

Let's make a few observations. Choosing any $n$ linearly independent edges adjacent to $A$ will always generate the tangent space $T_A(K)$, but only provided $R={\bf R}$. On the other hand, we can think of an irregular mesh for which $R={\bf Z}$ is inapplicable. For example, for any two chosen edges $a,b$, a third edge might not be an integral linear combination of $a,b$. Furthermore, if there are $k$ edges adjacent to $A$, then $R={\bf Z}_p$ is inapplicable unless $p>k$. Consequently, $R={\bf Z}_2$ work only when there is a single edge at every vertex $A$, i.e., never.

Exercise. If ${\bf R}^2$ is represented as a realization of the cell complex of the regular hexagonal grid, what algebra do its tangent spaces inherit? Define the tangent spaces and prove the analogue of the proposition above. What difference does the choice of ring $R$ make? Consider other grids on ${\bf R}^2$.

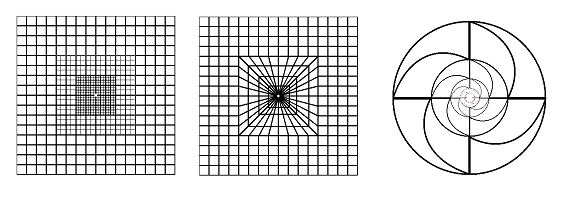
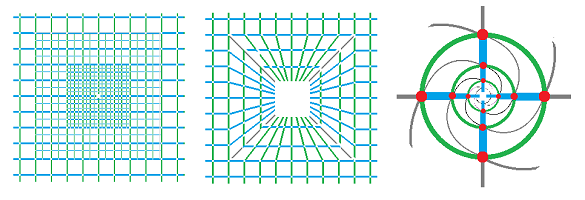
Now, what if we are to represent an open subset $U$ of ${\bf R}^n$ as a realization of a cell complex? Since such a set isn't compact, we still need an infinite complex. For example, if $U:={\bf R}^2 \setminus \{0\}$ is the punctured plane, there are many choices:

The first is made of squares but it's not a cubical complex; the second is but its edges aren't all aligned with the axes; the third is a triangulation but its edges are curved. Just as above, we can define the tangent spaces following the algebra of the ambient Euclidean space.

Every edge $a$ in $St_K(A)$ is represented by a parametric curve: $$p:[0,1]\to |K|,\ p(0)=A, p([0,1])=a,$$ which is regular: $p$ is continuously differentiable and $p'\ne 0$. Then, just as in the continuous case, we associate to the edge $a$ a vector in ${\bf R}^n$ given by $p'(0)$. This map, $$D:St_K(A)\to {\bf R}^n,$$ supplies the star with algebra of edges.

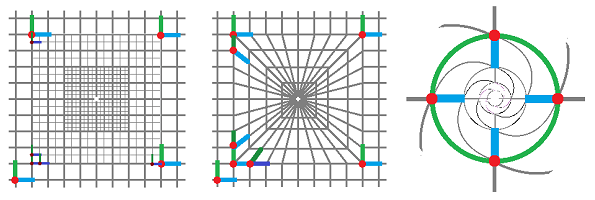
Some of the bases of the tangent spaces are shown below:

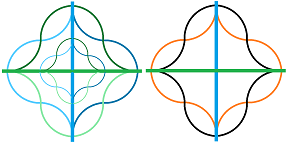
A cell complex representation of an open disk:

Next we apply the equivalence relation of balance, $$(A,AB)\sim -(B,BA),$$ to the disjoint union of the tangent spaces to create the tangent bundle of complex $K$: $$T(K):=\bigsqcup T_A(K) /_\sim.$$

Definition. A locally finite cell complex is called Euclidean of dimension $n$ if

• its realization is an open subset of ${\bf R}^n$;
• its tangent spaces are isomorphic to $R^n$;
• its tangent spaces have compatible bases: if $AB$ is the $i$th element of the basis of $T_A(K)$, then $-BA$ is the $i$th element of $T_B(K)$.

Then these elements of $T(K)$ are denoted by $dx_i$.

One can see the $dx$ in blue and $dy$ is green below:

The following are more complicated cases of the punctured plane:

Another one:

Algebra of forms

Let's review. Continuous and discrete $1$-forms in the $2$-space are functions of

• $x$, $y$, and
• $dx$, $dy$,

that are linear on $dx$, $dy$. They are represented by the formula in the last subsection: $$\varphi = f dx + g dy.$$

What are their algebraic properties?

Consider replacing $dx$ and $dy$ in $\varphi$ by $dx + dx'$ and $dy + dy'$. Then, $$f (dx + dx') + g(dy + dy') = (f dx + g dy) + (f dx' + g dy'),$$ where the coefficients are functions of $x,y$. That's additivity.

Let $\alpha \in R$ and consider replacing $dx$ with $\alpha dx$ and $dy$ with $\alpha dy$ in $\varphi$. In this case we get $$f(\alpha dx) + g(\alpha dy) = \alpha f dx + \alpha g dy = \alpha(f dx + g dy).$$ That's homogeneity.

What about $2$-forms? Given $\varphi = f dx \hspace{1pt} dy$, lif we try to verify additivity, we compute $f (dx + dx')(dy + dy')$. We get too many terms; no match! If we try to verify homogeneity, we compute $f (\alpha dx)(\alpha dy) = \alpha^2 f dx \hspace{1pt} dy$, we have no match! Conclusion: the $2$-forms aren't linear! In some sense, however, they are linear: linear on $dx$ and, separately, linear on $dy$. That's multilinearity.

Recall that forms are also supposed to be anti-symmetric. In particular, for $2$-forms, this means the equivalence of these forms: $$dx \hspace{1pt} dy = -dy \hspace{1pt} dx.$$ It also follows that $$dx \hspace{1pt} dx= dy \hspace{1pt} dy=0.$$

Exercise. Explain why $dx \hspace{1pt} dx$ and $dy \hspace{1pt} dy$ don't appear in the representation of $2$-forms. Hint: it's not because they are equal to zero.

Indeed, differential forms are multilinear antisymmetric functions parametrized by location in an $n$-manifold $X$ or a complex $K$.

The two types we have considered:

• Euclidean forms: $\Omega^k({\bf R}^n)$, and
• cubical forms/cochains: $C^k({\mathbb R}^n)$.

are modules under the usual addition and scalar multiplication of functions.

Exercise. Verify that the multilinearity and the antisymmetry are preserved under these operations.

We can also see the formula $$\varphi = f dx + g dy$$ as a representation of an arbitrary $1$-form as a linear combinations of $dx,dy$. We do not think, of course, of those as variables anymore but as two “basic” forms.

In $3$-space, we have:

• location variables: $x,y,z$;
• direction variables: $v_x,v_y,v_z$, and possibly $v'_x,v'_y,v'_z$ etc.

What are the $0$-forms? They are just functions.

What about $1$-forms? To understand the meaning of $dx$ and $dy$ in ${\bf R}^2$, we observe that they are $1$-forms: $$dx,dy:{\bf R}^2 \times R^2 \to R,$$ or, in the discrete case, $$dx,dy:{\bf Z}^2 \times R^2 \to R,$$ given by $$dx(x,y,v_x,v_y)=v_x,$$ $$dy(x,y,v_x,v_y)=v_y.$$ What makes these especially simple is that their values are independent of location.

Now, what about the rest of $1$-forms? They are to be found all as $$\varphi^1=fdx+gdy,$$ where $f=f(x,y),g=g(x,y)$ are just functions. Then, $$\varphi^1(x,y,v_x,v_y)=f(x,y) \cdot v_x+g(x,y) \cdot v_y.$$ It is common to omit $(x,y)$ throughout.

Exercise. Evaluate $x^2dx^1$ at $(3,2,1)$ in the direction of $(1,2,3)$.

We have previously defined the wedge product of forms. In particular, we have: $$dx\wedge dy:=dx \hspace{1pt} dy.$$ The wedge product operator $$\wedge : \Omega^1 \times \Omega^1 \to \Omega^{2},$$ is linear on either of the two components. Then, $$\varphi^1\wedge\psi^1=(Adx+Bdy)\wedge(Cdx+Ddy)$$ $$=(AD-BC)dxdy=\det \left[ \begin{array}{ccc} A & B \\ C & D \end{array} \right] dxdy. $$

Proposition. For dimension $3$, the bases of the spaces of differential forms of each degree are:

• $\Omega ^0({\bf R}^3),\ C^0({\mathbb R}^3) : \{1\}$;
• $\Omega ^1({\bf R}^3),\ C^1({\mathbb R}^3) : \{dx,dy,dz\}$;
• $\Omega ^2({\bf R}^3),\ C^2({\mathbb R}^3) : \{dxdy,dydz,dxdz\}$;
• $\Omega ^3({\bf R}^3),\ C^3({\mathbb R}^3) : \{dxdydz\}$;
• $\Omega ^k({\bf R}^3)=C^k({\mathbb R}^3) =0$ for $k>3$.

Exercise. Prove the proposition.

Exercise. Express the wedge products of the basic forms in terms of the higher order basic forms and give the matrix of this operator.

Previously we proved the following.

Theorem. The wedge product is associative.

Theorem. The wedge product is skew-commutative. Suppose $\varphi \in \Omega^k$ and $\psi \in \Omega^m$. Then $$\varphi \wedge \psi = (-1)^{km}\psi \wedge \varphi.$$

We refer to the forms $$dx,dy,dz, dx \wedge dy,...$$ as the basic forms. As all forms appear to be “linear combinations” of these, such a term makes sense. However, the coefficients in these linear combinations are functions and we can't think of these forms as a basis of $\Omega ^k(X)$ -- as an $R$-module. However, it is often beneficial to look at $\Omega ^k(X)$ as a module over the ring of functions $f:X\to R$: $$\varphi=\sum_i f_i dX_i,$$ where $dX_i$ are some basic forms of degree $k$.

Exercise. Explain why, if we adopt this point of view, the function $d:f\mapsto fdx$ isn't a linear operator anymore.

The exterior derivative of forms

What may be the meaning of the derivative of a differential form?

What we are used to is that the derivative of a function is also a function. This time we will rely on the hierarchy of forms and declare that:

• a function is a $k$-forms but its derivative is a $(k+1)$-form.

We arrive to this conclusion from the well-known relationship: $$df = f'(x)dx,$$ which is saying that the exterior derivative of the $0$-form $f$ is the $1$-form $f'(x)dx$. In dimension $3$, the exterior derivative of a $0$-form $f$ is a $1$-form given by $$df = f_x dx + f_y dy + f_z dz,$$ where $f_x$, $f_y$, and $f_z$ are the partial derivatives of $f$.

Meanwhile, the exterior derivative of a cubical form $f$ of degree $0$ in $3$-space is given by the same formula except the partial derivatives are simply the differences of values: $$f_x(n,\cdot,\cdot)= f(n+1,\cdot,\cdot)-f(n,\cdot,\cdot), ...$$

Since we already know the meaning of the exterior derivative of $0$-forms, we also know the exterior derivatives of the coefficient functions of any form. Now we define the exterior derivative, computationally, for the general case. The idea comes from the example above.

Definition: Suppose a $k$-form $\varphi$ is a linear combination of the basi $k$-forms. Then the exterior derivative of $\varphi$ is a $(k+1)$-form $d \varphi $ obtained from this linear combination by replacing each coefficient function $f$ with $df\wedge$.

The definition equally applies to both Euclidean and cubical forms. For the former, we will verify that the definition produces results that match the integral theorems of calculus. For the latter, we will confirm that the results match the standard definition of the exterior derivative as the dual of the boundary operator.

Now, for a $1$-form in $3$-space $$\varphi = F dx + G dy + H dz,$$ we compute omitting $\wedge$: $$\begin{align*} d \varphi &= (F_x dx + F_y dy + F_z dz)dx+(G_x dx + G_y dy + G_z dz)dy+(H_x dx + H_y dy + H_z dz)dz \\ &= (F_y dy \hspace{1pt} dx + F_z dz \hspace{1pt} dx) + (G_x dx \hspace{1pt} dy + G_z dz \hspace{1pt} dy) + (H_x dx \hspace{1pt} dz + H_y dy \hspace{1pt} dz) \\ &= (G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx. \end{align*}$$ We recognize these coefficients as those of the curl: $$\operatorname{curl}(F,G,H) = (G_x - F_y,H_y - G_z,F_z - H_x).$$ We have proven the following.

Proposition. $$d\left(<(F,G,H), (dx,dy,dz)>\right)=<\operatorname{curl}(F,G,H),(dxdy,dydz,dzdx)>.$$

Exercise. Confirm that the formula holds for cubical forms.

The result matches Kelvin-Stokes Theorem: $$\oint_{\partial\Sigma} Fdx+Gdy+Hdz = \iint_{\Sigma}\left\{(G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx\right\}$$ We must be on the right track!

Let's restate the above formula for $0$-forms. We recognize the coefficients as those of the gradient: $$\operatorname{grad} F = (F_x, F_y,F_z).$$ We have the following.

Proposition. $$dF=<\operatorname{grad}F,(dx,dy,dx)>.$$

Consider a $2$-form which is a linear combination of $dxdy$, $dydz$, and $dzdx$ whose coefficients are the functions to differentiate. Let $$\varphi = Adxdy + Bdydz + Cdzdx.$$ Then $$\begin{align*} d \varphi &= dA dx dy + dB dy dz + dC dz dx\\ &= (A_xdx+A_ydy+A_zdz)dxdy+...\\ &= (A_x dxdxdy + A_y dydxdy + A_z dzdxdy)+... \\ &= (0+0+A_z dzdxdy)+...\\ &= A_z dzdxdy + B_x dxdydz + C_y dydzdx\\ &= (A_z + B_x + C_y )dxdydz.\\ \end{align*}$$ We recognize the coefficient as the divergence: $$\operatorname{div} (B,C,A) = B_x + C_y + A_z.$$ Each term in the form is associated with the missing variable: $dxdy \to z$. We have proven the following.

Proposition. $$d\left(<(A,B,C),(dxdy,dydz,dzdx)>\right)=\operatorname{div} (B,C,A)dxdydz.$$

Exercise. Confirm that the formula holds for cubical forms.

The result matches Gauss' Theorem: $$\iiint_{R} \operatorname{div} F dV = \iint_{\partial R} F \cdot N dA.$$

Exercise. Show that for dimension $2$, we have: $$d\left(<(F,G),(dx,dy)>\right)= (G_x - F_y) dx \hspace{1pt} dy. $$

Now for degree $3$. If $\varphi = F dx \hspace{1pt} dy \hspace{1pt} dz$, then $$\begin{align*} d \varphi &= dF \cdot dx \hspace{1pt} dy \hspace{1pt} dz \\ &= (F_x dx + F_y dy + F_z dz) dx \hspace{1pt} dy \hspace{1pt} dz \\ &= F_x dx \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz + F_y dy \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz + F_z dz \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz \\ &= 0 + 0 + 0=0. \end{align*}$$ We have proven the following.

Proposition. $$d\left(F dx \hspace{1pt} dy \hspace{1pt} dz\right)=0.$$

Exercise. Use the above definition to prove that in ${\bf R}^n$, we have $$d( F dx_1 ... dx_n) = 0.$$

Exercise. Compute $df$, where $f=x^1+2x^2+...+nx^n$, at $(1,2,...,1)$ in the direction of $(1,-1,...,(-1)^{n-1})$.

Exercise. Prove that in ${\bf R}^n$, $$df^1 \wedge ... \wedge df^n(x) = \det \frac{\partial f^i}{\partial x^j}(x)dx^1 \wedge ... \wedge dx^n.$$

Exercise. Write the form $df$, where $f(x) = (x^1) + (x^2)^2 + ... + (x^n)^n$, as a combination of $dx^1,...,dx^n$.

Another way to write the definition is as follows. Suppose we are given $$\varphi = A dX \in \Omega^k,$$ where $A$ is function and $dX$ is a basis element of $ \Omega^k$ (could be $dx,dy$, or $dxdy,dydz$, etc). Then, we define $$d\varphi := dA \wedge dX$$ and then extend this definition to sums of terms of this kind.

The product rule for exterior derivative

Theorem. The exterior derivative $d : \Omega^k \to\Omega^{k+1}$ is a linear operator: $$d(a \varphi + b \psi) = a d\varphi + b d\psi, \ a, b \in R, \ \varphi, \psi \in \Omega^k.$$

Exercise. Prove the theorem.

Now we are interested in an analogue of the Product Rule from Calculus 1 -- for the wedge product. In other words, we want to find $d(\varphi \wedge \psi) = ?$ in terms of $d \varphi$, $d \psi$, $\varphi$, $\psi$.

First, for $0$-forms $\varphi, \psi$, we have the familiar Product Rule: $$(\varphi \psi)' = \varphi ' \psi + \varphi \psi '.$$ It can be rewritten for the exterior derivative: $$d(\varphi \psi) = d\varphi \psi + \varphi d \psi,$$ or $$d(\varphi \wedge \psi) = d\varphi \wedge \psi + \varphi \wedge d \psi,$$ This gives us an idea what the general rule should look like: the sum of the wedge products, in the same order.

Next, we continue with a $k$-form $\varphi$ and an $m$-form $\psi$. We assume that

• $\varphi = A dX$ and
• $\psi = B dY$,

where $A,B$ are functions and $dX,dY$ are some basic $k$- and $m$-forms respectively. Those could be $dx,dy$, or $dxdy,dydz$, etc. Then, by definition of exterior derivative, we have

• $d\varphi = dA \wedge dX$ and
• $d\psi = dB \wedge dY$.

In addition to this, we'll use the skew-commutativity of $\wedge$: $$f^k \wedge g^m = (-1)^{km} g^m \wedge f^k.$$

With that, we compute $$\begin{align*} d(\varphi \wedge \psi) &= d(A dX \wedge B dY) \\ \text{linearity of } \wedge ... &=d(AB dX \wedge dY) \\ \text{definition of } d ... &=d(AB) \wedge dX \wedge dY \\ \text{Product Rule} ... &=(A dB + B dA) \wedge dX \wedge dY \\ &=A dB \wedge dX \wedge dY + B \wedge dA \wedge dX \wedge dY \\ \text{skew-commutativity} ... &=(-1)^{1 k}A dX \wedge dB \wedge dY + dA \wedge dX \wedge B \wedge dY \\ \text{substitute} ... &=(-1)^k \varphi \wedge d \psi + d \varphi \wedge \psi. \end{align*}$$

Since we have proven the formula for the basic forms, we have proven it for all forms.

Theorem (Product Rule -- Leibniz Rule). $$d(\varphi^k \wedge \psi^m) = d \varphi^k \wedge \psi^m + (-1)^k \varphi^k \wedge d \psi^m.$$

Exercise. What in the proof needs to be changed to make it applicable to cubical forms?

The topological property of the exterior derivative

As we have seen, the property

the boundary of the boundary is zero,

implies

the exterior derivative of the exterior derivative is zero.

In other words, $$\partial\partial=0 \Rightarrow dd=0.$$ To clarify, we make these two operators distinct by adding subscripts. Then our theorem is restated: $$d_{k+1}d_k=0 : \Omega^k \to \Omega^{k+2},\ k=1,2...$$ The composition of these linear operators is trivial.

Let's prove this property in $3$-space using the formulas above.

First, $0$-forms. Suppose $F$ is a twice continuously differential function of $3$ variables. Then, $$\begin{array}{lll} ddF = d(F_xdx+F_ydy+F_zdz) & \text{...by the first formula}\\ =dF_xdx+dF_ydy+dF_zdz\\ =(F_{xx}dx+F_{yx}dy+F_{zx}dz)dx+... & \text{... by the second formula}\\ =(F_{xx}dxdx+F_{yx}dydx+F_{zx}dzdx)+...\\ =(0+F_{yx}dydx+F_{zx}dzdx)+... & \text{... by anti-symmetry}\\ =(F_{yx}dydx+F_{zx}dzdx)+(F_{xy}dxdy+F_{zy}dzdy)+(F_{xz}dxdz+F_{yz}dydz)\\ =(-F_{yx}+F_{xy})dxdy+(-F_{zy}+F_{zy})dydz+(-F_{zx}+F_{xz})dxdz & \text{... by anti-symmetry}\\ =0dxdy+0dydz+0dxdz & \text{... as all the mixed derivatives}\\ & \quad\text{are equal by Clairaut's theorem}\\ =0. \end{array}$$

For $1$-forms, let's just inspect the results of a single differentiation: $$d(F dx + G dy + H dz) = (G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx.$$ To get to $0$, we apply now the third formula, anti-symmetry, and Clairaut's theorem.

Exercise. Use the formulas from the last section to prove that the composition of the exterior derivative $dd : \Omega^1({\bf R}^3) \to \Omega^3({\bf R}^3)$ is $0$.

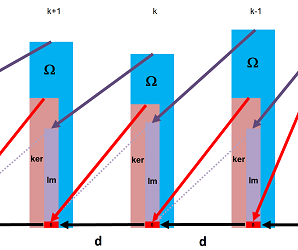
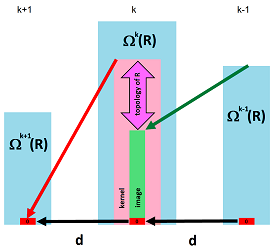
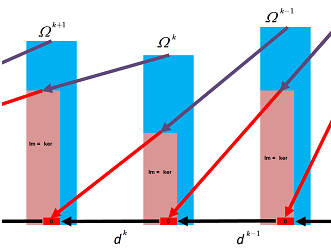
We restate the diagram of all exterior derivatives from the last section: $$\newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrr} 0& \la{d=0} & \Omega^N(X) & \la{d_{N-1}} & ... & \la{d_0} & \Omega^0(X) &\la{d=0} &0 . \end{array} $$ where $X$ is a region in ${\bf R}^N$. This sequence of vector spaces and linear operators is called the de Rham complex of $X$. With the property $dd=0$, it is, of course, a cochain complex. The construction is illustrated below.

This is pure linear algebra!

Exercise. State and prove versions of the above theorems for subsets of the Euclidean space.

We combine the above theorems into one.

Theorem (Topological Property of Exterior Derivative). If $\varphi$ is a form in $\Omega ^k({\bf R}^n)$ with twice continuously differentiable coefficients, then $d_{k+1}(d_k \varphi)=0$.

Proof. As before, assume $\varphi = A dX$ (and use linearity later), where $dX$ is a basic $k$-form and $A=A(x^1,...,x^n)$ is a coefficient function, twice continuously differentiable. Then, using the definition of exterior derivative and its formula for $0$-forms, we have: $$\begin{align*} d \varphi &= d(A dX) \\ &= dA \wedge dX) \\ &=\left( \sum _{i=1}^{n} A_i dx^i \right) \wedge dX \\ &=\sum _{i=1}^{n} A_i \left( dx^i \wedge dX \right). \end{align*}$$ Next, $$\begin{align*} d (d \varphi) &= d \left( \sum _{i=1}^{n} A_i dx^i \wedge dX \right) \\ {\rm linearity...}\quad &= \sum _{i=1}^{n} d \left( A_i dx^i \wedge dX \right) \\ {\rm definition...}\quad &= \sum _{i=1}^{n} [ d A_i ] \wedge dx^i \wedge dX \\ {\rm formula...}\quad &=\sum _{i=1}^{n} \left[ \sum _{j=1}^{n} A_{ji} dx^j \right] \wedge dx^i \wedge dX \\ &= \left[ \sum _{i=1}^{n} \sum _{j=1}^{n} A_{ji} dx^j \wedge dx^i \right] \wedge dX . \end{align*}$$ Next we need to show that $[...]=0$. It is the case because of antisymmetry and the fact that mixed derivatives are equal:

• each pair $(i,j)$ with $i\ne j$ appear twice in the sum -- in the opposite order, so they cancel;
• pairs $(i,i)$ appear $n$ times with each equal to $0$.

We can see this effect if we put the terms of the sum in a table: $$ \begin{array}{cccccc} & & ... & i & ... & j & &\\ &... & ... & ... & ... & ... &\\ & i & ... & A_{ii}dx^idx^i & ... & A_{ji}dx^jdx^i& &\\ & ...& ... & ...& ... & ...& &\\ & j & ... & A_{ij}dx^idx^j & ... & A_{jj}dx^jdx^j & &\\ \end{array} $$ $\blacksquare$

We will deal with the kernel and the image separately, for now.

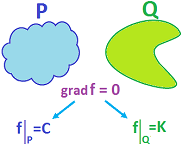
Definition. If $d \varphi = 0$, then $\varphi$ is called closed.

Definition. If for some $\psi$, $\varphi = d \psi$, then $\varphi$ is called exact.

So,

• $\ker d_k$ is the set of all closed $k$-forms;
• $\operatorname{Im} d_{k-1}$ is the set of exact $k$-forms.

All are subspaces: $$\operatorname{Im} d_{k-1} \subset \ker d_k \subset \Omega^{k}.$$

The above theorem can be restated as follows.

Theorem. All exact forms are closed.

When the converse is true -- all closed forms are exact -- the sequence is exact. In this case, as we shall see, the topology of ${\bf R}^n$, of this dimension, is trivial. In fact, it is in the “gap” between $\operatorname{Im} d_{k-1}$ and $\ker d_k$ where information about the topology of of the region is to be found:

An approach we have used to evaluate the gap between two vector spaces is to look at the difference of their dimensions. Unfortunately, in the setting of differential functions and forms, the dimensions of $\operatorname{Im} d_{k-1}$ and $\ker d_k$ are infinite. That's why it is unavoidable that we have to deal with their quotient, $$\ker d_k / \operatorname{Im} d_{k-1}$$ called the de Rham cohomology.

Closedness and exactness of $0$-forms

Theorem. A $0$-form in ${\bf R}$ is closed if and only if it is constant.

Proof. ($\Rightarrow$) If $\varphi^0$ is constant, then $d\varphi^0 = 0$, so $\varphi$ is closed.

($\Leftarrow$) Suppose $d\varphi^0 = 0$ and suppose $\varphi^0 = f \in C^1$. In ${\bf R}^1$, $df(x) = f'(x) dx = 0 dx =0$. Then, by a certain corollary to the Mean Value Theorem, $f$ has to be constant. $\blacksquare$

What about something more general than ${\bf R}$?

We consider $\Omega^k(D)$, which is the space of forms with domains in an open region $D$. We notice that this theorem works for $\Omega^0({\bf R})$, and for $\Omega^0((0,1))$ and $\Omega^0((2,3))$, but it does not work for $\Omega^0((0,1) \cup (2,3))$. Indeed, consider $$f(x) = \begin{cases} 1, & \mbox{for } x \in (0,1),\\ 2, & \mbox{for } x \in (2,3). \end{cases}$$ It is not constant, but $df = 0$.

So, when does it work?

Theorem. If the domain $D \subset {\bf R}^n$ is path-connected, then closed $0$-forms are constant functions (and vice versa).

What about exact $0$-forms? Too easy: $\varphi^0 = d \psi^{-1}$ (where $-1$ is the degree of the form), but all $\psi^{-1}=0$, so $\varphi^0=0$.

We have the following then.

Proposition. The only exact $0$-form in ${\bf R}^n$ is $0$.

Things are more complicated as we move to multidimensional spaces.

However, even in ${\bf R^n}$ we still have the following.

Theorem. Constant forms are closed.

Exercise. Prove the theorem.

The converse was easy to prove for the discrete case. We will use the idea of that proof with the help of the following theorem.

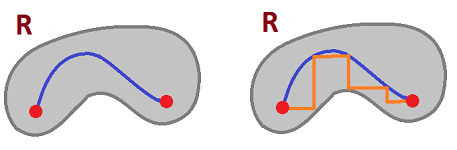
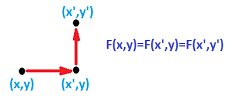
Theorem. In an open region $D \subset {\bf R}^n$, if two points are connected by a path, they can be connected by a step-path, with edges parallel to the coordinate axes (a “discrete curve”).

Proof. First, what if $R$ is a disk?

Since it's round, the solution is simple:

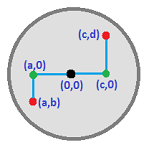
Lemma: In a disk, we can always get from $(a,b)$ to $(c,d)$ by a step-path with no more than $4$ steps: $$(a,b)\to (a,0) \to (0,0)\to (c,0)\to (c,d).$$

Based on the lemma, the construction for a general $D$ looks like this.

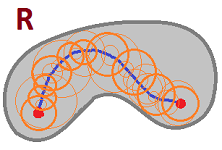
We cover the path between $A$ and $B$ with disks $D_1,...,D_n$, within $R$, and then apply the lemma $n$ times:

• from $A=A_0$ to any $A_1 \in D_1 \cap D_2$ within disk $D_1$,
• then from $A_1$ to any $A_2 \in D_2 \cap D_3$ within disk $D_2$,
• $\ldots$,
• from $A_{n-1}$ to $A_n=B$ within disk $D_n$.

This should work, but how do we know that we can get there in a finite number of steps?

This is not a problem... For each point on the path, find an open disk in $D$ centered at that point. The path, image of $[0,1]$ under a continuous $p$, is compact, therefore this cover has a finite subcover... etc. $\blacksquare$

Exercise. Finish the proof.

Exercise. Find a proof that doesn't invoke compactness.

This is what we are after.

Theorem. If the domain $D$ is open and path-connected, closed $0$-forms are constant.

Proof. The proof is for ${\bf R^2}$ but equally applicable to all dimensions.

Suppose $D$ is the domain and $F$ is a closed $0$-form, i.e., just a function of two variables. Then $\operatorname{grad} F(dx,dy) = 0$; therefore, $F_x=0$ and $F_y=0$. Then we have the following.

• (1) $F_x=0$ for all $(x,y) \in D$. Hence, $F$ is constant with respect to $x$ on $R$.
• (2) $F_y=0$ for all $(x,y) \in D$. Hence, $F$ is constant with respect to $y$ on $R$.

So what?

• (1) $\Rightarrow$ $F$ is constant on every segment $=D \cap$ horizontal line; with possibly different constants!
• (2) $\Rightarrow$ $F$ is constant on every segment $=D \cap$ vertical line; with possibly different constants!

What we have shown is that $F$ is constant on each of these segments:

The values of these constants, of course, may be different. However, as we make turns, we don't change them:

So, if there is a path between $(x_0,y_0), (x_1,y_1)$ made of horizontal and vertical segments, then $F(x_0,y_0) = F(x_1,y_1)$. How can we use this?

Idea: approximate the path with a step-like path with the same endpoints -- by the last theorem. $\blacksquare$

The proof won't work if $D$ isn't open. However, this isn't a real restriction because we usually avoid doing calculus on domains that aren't open because we want the derivative to be well defined.

Closedness and exactness of 1-forms

Let's review more of the related material as presented in calculus 1 and use the ideas later.

This is how we used to solve the “exactness problem”. Given a continuous function $f$, it is exact if it's the derivative of someone: $$f=F'.$$ In other words, there is an antiderivative of $f$. We can construct $F$ using nothing but continuity. Indeed $f$ is integrable on $[a,b]$ and its Riemann integral exists on all intervals within $[a,b]$. Therefore we can define $F=d^{-1}f$ via integration as follows: $$F(x)=\int _a ^x f(x)dx,\ x \in [a,b].$$ This is the idea, and the proof of, a version of the Fundamental Theorem of Calculus. It will be used again for $1$-forms.

We deal with closed and exact $1$-forms in ${\bf R}^1$ first. All $1$-forms in ${\bf R}^1$ look the same: $\varphi = f(x) dx$, where $f$ is some function.

Question: When is such a $\varphi$ closed? When $d \varphi = 0$?

Answer: Always! There are no non-trivial $2$-forms, as we know.

Question: When is such a $\varphi$ exact? When $\varphi = d \psi$?

If $d \psi = f(x) dx$, then $\psi$ is a $0$-form. And, in fact, $$\psi(x)=F(x) = \displaystyle\int f(x) dx,$$ i.e., $\psi$ is an antiderivative of $f$.

Answer: When $f$ is integrable.

Conclusion: $$\ker d_1 = \operatorname{Im} d_0,$$ for all continuous $1$-forms in ${\bf R}^1$.

The issue isn't as simple in ${\bf R}^2$.

All $1$-forms in ${\bf R}^2$ look like this: $$\varphi = f dx + g dy,$$ where $f=f(x,y),g=g(x,y)$ are functions of two variables.

Question: When is such a $\varphi$ closed?

Let's compute! $$\begin{align*} d \varphi &= df \hspace{1pt} dx + dg \hspace{1pt} dy \\ &= (f_x dx + f_y dy)dx + (g_x dx + g_y dy)dy \\ &= f_y dy \hspace{1pt} dx + g_x dx \hspace{1pt} dy \\ &= (g_x - f_y) dx \hspace{1pt} dy \end{align*}$$ Note that this expression is the rotation, $\operatorname{rot}$, which is the integrand in the right-hand side of Green's theorem.

The above computation implies the following theorem.

Theorem. $\varphi = fdx + gdy$ is closed if and only if $g_x=f_y$.

In other words, $$\ker d_1 =\{\varphi = fdx + gdy:g_x=f_y\}.$$

Question: When is $\varphi= fdx + gdy$ exact? When $\varphi = d \psi$?

Here $\psi$ is simply a function of two variables. Then, we conclude that $$\psi _x=f,\psi _y =g.$$ And, further, $$\psi =\int f(x,y)dx, \psi =\int g(x,y)dy.$$

Example. We choose a closed form: $$\varphi = \left(x^2y + x\right)dx + \left(\frac{1}{3}x^3 + y\right) dy.$$ Indeed, if we set $f := x^2y+x$ and $g := \frac{1}{3}x^3 + y$, we have $f_y=x^2$ and $g_x=x^2$. Therefore $\varphi$ is closed.

Now exactness. It is exact when $\varphi = d \psi$ for some $\psi$, a $0$-form. Now, if $\psi = F(x,y)$, then $\varphi = d \psi = F_x dx + F_y dy$. Therefore $$F_x = x^2y + x, F_y= \frac{1}{3} x^3 + y$$ Now we integrate to get $$F= \frac{x^3}{3}y + \frac{x^2}{2} + C(y), F = \frac{1}{3}x^3y + \frac{y^2}{2} + K(x).$$ We conclude that $$F(x,y) = \frac{1}{3}x^3y + \frac{x^2}{2} + \frac{y^2}{2} + M,$$ for any constant $M$.

$\square$

So, this closed form is exact. Is it always the case?

The answer is below.

Theorem (Poincare Lemma). Every closed $1$-form with continuously differentiable coefficients in ${\bf R}^n$ is exact.

The meaning of the theorem is that our cochain complex is exact at dimension $1$:

Proof. The proof is based on the same idea, integration with a variable upper limit, as in the version of the Fundamental Theorem of Calculus discussed above. We will prove it for $n=2$.

Given a $1$-form $\varphi =fdx+gdy$ we construct a $0$-form $\psi$ with $d\psi =\varphi$ as a line integral. We fix a point $a \in {\bf R}^n$ and define $\psi$ as a function of $u=(x,y)$: $$\psi (u):=\int _C \varphi,$$ where $C$ is any path from $a$ to $u$.

Is this function well defined? To be well defined, $\psi$ should be independent of our choice of path $C$. There may be many paths from $a$ to a given $u$ and they all should produce the same value to be assigned to $\psi (u)$.

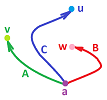
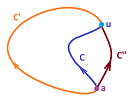
Suppose we have another path $C'$ from $a$ to $u$ that doesn't intersect $C$ except at the end points. Then we need to prove that $$\int _C \varphi = \int _{C'} \varphi.$$ Of course, by paths we understand parametric curves. The idea is to form a closed path from $a$ to $a$ from these two: $K=C \cup -C'$, where $-C'$ is $C$ parametrized in the opposite direction.

Then, on the one hand, we compute $$\int _K \varphi =\int_C \varphi + \int _{-C'} \varphi = \int_C \varphi - \int _{C'} \varphi.$$ On the other hand, $$\int _K \varphi = \iint _D (g_x-f_y)dxdy ,$$ where $D$ is the region bounded by $K$, by Green's theorem. Therefore the integral is zero because the form $\varphi =fdx+gdy$ is closed. It follows then that $$\int_C \varphi - \int _{C'} \varphi =0.$$

Finally we differentiate the integral which is just a function: $$d\psi = \psi _x dx + \psi _y dy = fdx+gdy.$$ The result follows from the Fundamental Theorem of Calculus for parametric curves.

$\blacksquare$

Thus, $$\operatorname{Im} \{d_0:\Omega ^0({\bf R}^n) \to \Omega ^1({\bf R}^n)\} = \ker\{d_1:\Omega ^1({\bf R}^n) \to \Omega ^2({\bf R}^n)\}.$$

However, this isn't the end of the story...

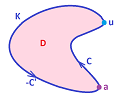
Example. Consider $$\theta = \frac{1}{x^2+y^2} (-ydx + xdy)$$

This one is closed. Indeed, the numerators of the partial derivatives are: $-(x^2+y^2) + y \cdot 2y = -x^2 + y^2$ and $-y^2 + x^2$. They cancel.

However, we accept this without proof, $\theta $ is not exact!

But how is this possible? Since we are dividing by $x^2+y^2$, we must be careful about the domain, $D$. Here, $D = {\bf R}^2 \setminus \{(0,0)\}.$

$\square$

Conclusion: It is not true that every closed $1$-form in ${\bf R}^2 \setminus \{(0,0)\}$ is exact.

What makes the difference is the topology of the region $R$.

Let's observe that in the example above the antiderivative of $\varphi$ is found to be $$F(x,y) = \frac{1}{3}x^3y + \frac{x^2}{2} + \frac{y^2}{2} + M,$$ for any constant $M$. If we think of $M$ as a function, it is the only closed $0$-form. So, if the derivative is the same then two forms differ by a closed form. More general result is the following.

Theorem. If $d \psi_1 = d \psi_2$, then $\psi_1 - \psi_2$ is a closed form.

Proof. It follows that $d(\psi_1 - \psi_2) = 0$, so $\psi_1 - \psi_2$ is closed as we use linearity of $d$. $\blacksquare$

Example. If $\varphi = x dx + x dy$, is it exact? We differentiate, to get $F_x = x$ and $F_y = x$. Then, $F = \frac{x^2}{2} + C(y)$ and $F = xy + K(x)$, which is impossible! So $\varphi$ is not exact. $\square$

De Rham cohomology

What is the relation between closed and exact forms and the topology of the region? Let's review what we have learned about this relation.

Our main conclusion is that the “difference” between the sets of closed and exact forms reveals the topology of the domain (and vice versa):

• path-connectedness via $0$-forms;
• simple-connectedness via $1$-forms.

Closed forms are constants, if $D$ is path-connected. But what if it's not? What if $D$ has two or more path components? Closed forms are the ones piecewise constant, i.e., constant on each path-component (with values that may differ from one component to the next):

Recall:

• The exterior derivative is a linear operator $d_0 \colon \Omega^0(D) \to \Omega^1(D)$;
• Closed $0$-forms = $\ker _0 d$, subspace of $\Omega^0(D)$.

Theorem. With real coefficients, for a path-connected region $D$, we have

• $\ker d_0 \simeq {\bf R}$.

Moreover, if $D$ has $p$ path-components, we have:

• $\ker d_0 \simeq {\bf R}^p$.

Recall also:

• The exterior derivative is a linear operator $d_1 : \Omega^1(D) \to \Omega^2(D)$;
• Closed $1$-forms give $\ker d_1$, a subspace of $\Omega^1(D)$;
• Exact $1$-forms give $\operatorname{Im} d_0$, a subspace of $\Omega^1(D)$.

Theorem. If $D \subset {\bf R}^n$ is simply connected, then every closed $1$-form is exact.

In other words, $$\operatorname{Im} d_0 = \ker d_1,$$ which together imply that there is no “hole”.

More generally, the “difference” between $\operatorname{Im} d$ and $\ker d$ is in the “dimensions” of these two spaces. If we subtract the dimensions, we “find” the topology of $D$, i.e., the number of holes.

Thus, the interaction between closed and exact forms reveals the topology of the domain.

In particular, for $0$-forms,

• $\dim \ker d -\dim\operatorname{Im} d$ = # of path-components.

Another way to see that is to consider ${\bf R}^n / {\bf R}^m = {\bf R}^{n-m}$.

Since $d_{k+1}d_k=0$, we have $$\operatorname{Im} d_k \subset \ker d_{k+1}.$$ So, it makes sense to define the equivalence class $$[\psi] \in \ker d_{k+1} / \operatorname{Im} d_k,$$ for $\psi\in\ker d_{k+1}.$ Then each class is given by: $$[\psi] = \psi + \operatorname{Im} d_k.$$ We have introduced an equivalence relation on closed forms:

two forms are equivalent -- cohomologous -- if their difference is exact.

Example. For $0$-forms, if $f$ and $g$ are functions and $f \sim g$, then $f-g = {\rm constant}$. Therefore, $f'=g'$. That's Calculus 1! $\square$

Definition. Suppose $D \subset {\bf R}^n$ is a region. The $k$th de Rham cohomology of $D$ is the following vector space: $$H_{dR}^k(D) := \ker d_k / \operatorname{Im} d_{k-1}.$$

Here's where this comes from: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \Omega^{k-1} & \ra{d_{k-1}} & \Omega^k & \ra{d_k} & \Omega^{k+1} \\ & & \cup & & \\ & & \ker d_k & & \\ & & \cup & & \\ & & \operatorname{Im} d_{k-1} & & \end{array} $$

Let's see what we can actually compute with the data that we have.

We do know a lot about $0$-forms. For a path-connected $D$, we have found everything about closed and exact forms. This is how we can compute the de Rham cohomology: $$\begin{align*} {\rm closed} \hspace{3pt} 0{\rm -forms} / {\rm exact} \hspace{3pt} 0{\rm -forms} &= {\rm constants} / 0 \\ &= {\rm constants} \\ &= {\bf R}. \end{align*}$$ Similarly:

• $H_{dR}^0(B(0,1) \cup B(3,1)) = {\bf R}^2,$
• $H_{dR}^0({\bf R}^n) = {\bf R}$;
• $H_{dR}^0(B((0,1)) = {\bf R}$;

etc.

This is not so simple with dimension $1$.

Frequently, we can prove that the domain is simply connected, then we have trivial $1$-cohomology: $$H_{dR}^1({\bf R}^3 \setminus \{0\})=0.$$

If it is not simply connected, we have less to say. For example, we know that the $1$-form $\frac{1}{x^2+y^2} (-ydx + xdy)$ is closed but not exact. Therefore, $$H_{dR}^1({\bf R}^1 \setminus \{0\})\ne 0.$$ It is in fact ${\bf R}$.

More examples of results that we can compute with some effort:

• $H_{dR}^1({\bf R}^3 \setminus \{0\}) = 0$;
• $H_{dR}^1({\bf R}^3 \setminus z-\text{axis})={\bf R}$.

For higher dimensions:

• $H_{dR}^k({\bf R}^n)=0,\ k=1,2,...$

But what about the torus, cone, pretzel, etc? For all of these, the de Rham cohomology coincides with the cohomology of the cell representations of these spaces.