This site is being phased out.
Forms
Contents
Work of force
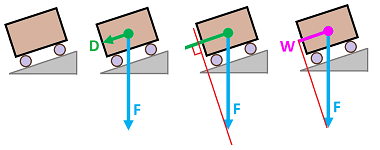
Suppose we want to compute the work of a constant force along a straight path. As we know in this case
This simple formula only works if we carefully take into account the direction of motion. For example, if you move forward and then back, the work breaks into two parts and they may cancel each other. The idea is that the work may be positive or negative and we should speak of displacement rather than distance. We then amend the formula as:
The need for considering directions becomes clearer when the dimension of the space is $2$ or higher. We use vectors.
Suppose $F$ is our force vector and $D$ is the displacement vector. Then this is what we know about the work of $F$. First, as we just saw, the work of the force is $$W = \pm F \cdot D \quad \text{ if } F || D,$$ and we have the plus sign when the two are collinear. Second, $$W = 0 \quad \text{ if } F \perp D.$$ Therefore, only the projection of $F$ on $D$ matters when calculating the work and it is the projection when the length of $D$ is $1$.
Then, the work $W$ of force $F$ along vector $D$ is defined to be: $$W := \langle F , D \rangle .$$ It is simply a (real-valued) linear function of the displacement, i.e., a covector.
As the force $F$ may vary from location to location, the need to handle the displacement vectors, i.e., directions, appears, separately, at every point of the Euclidean space. The set of all possible directions at point $A\in {\bf R}^n$ form a vector space of the same dimension. It is $V_A$, a copy of ${\bf R}^n$, attached to each point $A$:
If we replace ${\bf R}$ with an arbitrary ring of coefficients $R$, $V_A$ is the $R$-module generated by some basis of ${\bf R}^n$, for each $A$. Meanwhile, the work $W$ is a linear map (determined by the force $F$) defined on this space.
Next, we apply this idea to cell complexes.
Directions in a cell complex
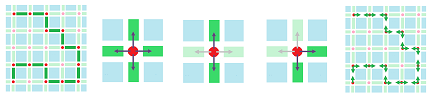
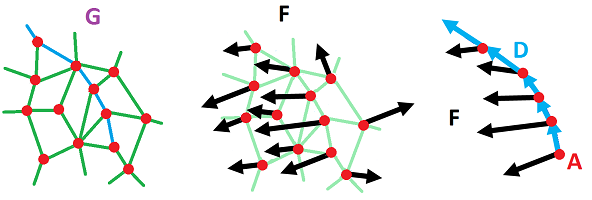
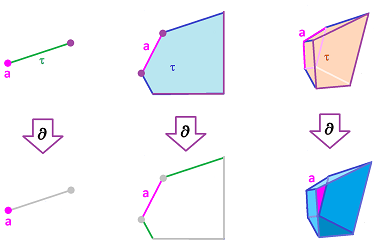
First, what is the set of all possible directions on a graph? We've come to understand the edges starting from a given vertex as independent directions. That's why we have as many vectors as there are edges at each of its points:
Of course, once we start talking about oriented cells, we know it's about chains, over $R$.
Definition. For each vertex $A$ in a cell complex $K$, the (dimension $1$) tangent space at $A$ of $K$ is the set of $1$-chains over $R$ generated by the $1$-dimensional star of the vertex $A$: $$T_A=T_A(K):=< \{AB \in K\} > \subset C_1(K).$$
Proposition. The tangent space $T_A(K)$ is a submodule of $C_1(K)$.
Next, a subcomplex $L\subset K$ inherits its tangents from the ambient complex.
Proposition. For each vertex $A$ in subcomplex $L\subset K$, the tangent space at $A$ of $L$ is the span in $T_A(K)$ of the set of edges in $L$ that originate from $A$: $$T_A(L):=< \{AB \in L \} > \subset T_A(K).$$
Exercise. Prove the proposition.
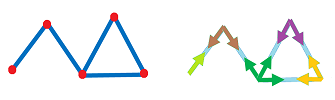
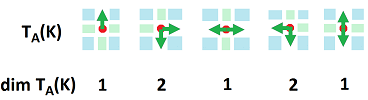
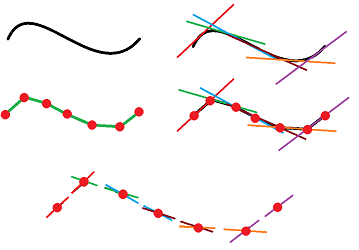
These are the dimensions of the tangent spaces of the discrete curve shown above:
Exercise. (a) Consider the rest of the points. (b) Provide examples, whenever possible, of points on a discrete curve $K$ in ${\bf R}^3$ with: $$\dim T_A(K)=0,1,2,3.$$
A local $1$-form is a $1$-cochain on the tangent space, i.e., a linear function $$\varphi_A: T_A\to R.$$
Then the work of a constant force along an edge in a cell complex is an example of such a form. Now, what if we have a force in complex $K$ that varies from point to point? Then the work along an edge -- as a direction of the displacement -- will depend on the location of the vector.
We capture this set of all possible directions in each location by attaching a tangent space $T_A$ to every point $A$ in $K$.
Let's review the setup. First, we have the space of locations $X=K^{(0)}$, the set of all vertices of a cell complex $K$. Second, to each location $A\in X$, we associate the space of directions determined by the structure of $K$, specifically, by its edges, $K^{(1)}$.
Now, while the directions at vertex $A\in K$ are given by the edges adjacent to $A$, we can also think of all $1$-chains in the star of $A$ as directions at $A$. They are subject to algebraic operations on chains and, therefore, form a module, $T_A$. We call it the tangent space $T_A$ of $K$ at $A$.
Furthermore, we record the work as a local $1$-form parametrized by location, i.e., a linear map on each star:
We collect the tangent spaces into the (dimension $1$) total tangent space of $K$: $$\{T_AK\}:=\bigsqcup _{A\in K} \left( \{A\} \times T_A \right).$$ Then $\varphi$ is a function on the total tangent space, $$\varphi=\{\varphi_A: \ A\in K\}:\{T_AK\} \to R$$ linear on each tangent space.
The work associates to every location and every direction at that location, a quantity: $$\varphi(A,AB)\in R.$$ The total work over a path in the complex is the line integral of $\varphi$ over a $1$-chain $a$ in $K$. It is simply the sum of the values of the form at the edges in $a$: $$\begin{array}{ll} a=&A_0A_1+A_1A_2+...+A_{n-1}A_n \Longrightarrow \\ &\int_a \varphi:= \varphi (A_0,A_0A_1)+\varphi (A_1,A_1A_2)+... +\varphi (A_{n-1},A_{n-1}A_n). \end{array}$$
If this number $\varphi(A,AB)$ is the work performed by a given force while moving from $A$ to $B$ along $AB$, let's look at it from the point of view of physics. Then the work carried out by the force from $A$ to $B$ should be the negative of the one carried out from $B$ from $A$: $$\varphi(A,AB)= -\varphi(B,BA).$$ It follows that the work defined separately on each of the stars will have matched values on the overlaps. Therefore, it is well-defined as a linear map on $C_1(K)$.
Theorem. A local form that satisfies the condition above is a $1$-cochain on $K$.
Exercise. Provide details of the proof.
This conclusion reveals a certain redundancy in the way we defined the space of all directions as the total tangent space $\{T_AK\}$. We then postulate that the direction from $A$ to $B$ is the opposite of the direction from $B$ to $A$: $$(A,AB)\sim -(B,BA).$$
This equivalence relation reduces the size of the space of all possible directions via the quotient construction. Below, we can see similarity between this new space and the space of tangents of a curve:
It looks as if the disconnected parts of $\{T_AK\}$, the tangent spaces, are glued together.
Theorem. The equivalence relation preserves the operations on each tangent space and, therefore, defines the module $\{T_AK\}/_{\sim}$, called the tangent bundle of $K$. Moreover, $$\{T_AK\}/_{\sim}=C_1(K).$$
Exercise. Prove the theorem.
Since there are no directions to consider, a $0$-form is simply a function of vertices, a $0$-cochain. What is the meaning of its derivative? It is supposed to show the local (i.e., within the edge distance) change of its value as we move from one location to the next. Then, the exterior derivative of a $0$-form is a $1$-form given by the familiar formula: $$(d f^0) (AB):=f(B)-f(A).$$
Stars and tangent spaces of cells
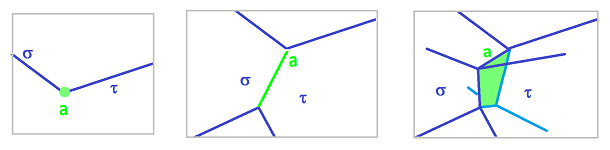
Let's consider other applications. Suppose a liquid flows through a $k$-dimensional cell complex. The $k$-cells (rooms) contain the liquid and it flows through $(k-1)$-dimensional cells (walls). The behavior of the flow is determined locally: for every $(k-1)$-cell $a$, we may ask how much of the liquid goes to an adjacent $k$-cell $\sigma$ (and $\tau$, and $\alpha$, etc.).
With the orientations of the cells given, such a function is a (local) $k$-form. In the case of $k=1$, it is defined on the chain complex of the star of the vertex $a$, as above. For the general case we use the following.
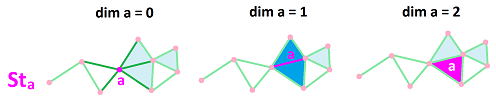
Definition. Given a $k$-cell $a$ in cell complex $K$, the star of $a$ is the set of all cells in $K$ that contain $a$ as their boundary cell: $$St_a=St_a(K):= \{\sigma \in K: a\in \partial \sigma\} \subset K.$$
Of course, the star doesn't have to be a subcomplex.
Exercise. Prove that its complement is. Hint: the star of cell $a$ doesn't contain cells of dimensions $m \le k$ except for $a$ itself.
Furthermore, the algebra of directions is conducted in the tangent space.
Definition. For each $k$-cell $a$ in a cell complex $K$, the tangent space at $a$ of $K$ is the set of $m$-chains, $m > k$, over $R$ generated by the star of $a$: $$T_a=T_a(K):=< St_a(K) > \subset C(K).$$
As before, a subcomplex $L\subset K$ inherits its tangents from the ambient complex.
Proposition. For each cell $a$ in subcomplex $L\subset K$, the tangent space at $a$ of $L$ is the span in $T_a(K)$ of the set of cell in $L$ that contain $a$: $$T_a(L):=< St_a(L) > \subset T_a(K).$$
Exercise. Prove the proposition.
As the cells of $K$ are split into two groups, we have the following.
Proposition. For every cell $a\in K$ we have $$C(K)=T_a(K) \oplus C(K\setminus St_a(K)).$$
Then the projection of the chain complex of the complex to the tangent space, $$P_a:C(K)\to T_a(K),$$ is generated by this identity for every cell $\tau\in K$: $$P_a(\tau):=\begin{cases} \tau & \text{ if } \tau\in St_a,\\ 0 & \text{ if } \tau \not\in St_a. \end{cases}$$
We can make the tangent space into a chain complex with the boundary operator given as the restriction of the boundary operator of $K$:
Proposition. We have: $$\partial = \partial \Big| _{T_a(K)} =P_a\partial i_a:T_a(K)\to T_a(K),$$ where $i_a:T_a(K)\to C(K)$ is the inclusion.
Exercise. Prove that $\partial$ is well-defined and that it satisfies $\partial\partial =0$.
In the case of simplicial complexes, the boundary operator of the tangent space has an explicit representation based on the cone construction.
Proposition. Suppose $A$ is a vertex in a simplicial complex $K$. Then, in $St_A(K)$ we have: $$\begin{array}{ll} \partial (A_0A_1... A_n) &= \sum_{i>0} (-1)^i A_0A_1... [A_i]... A_n\\ &=A\cdot \partial (A_1... A_n). \end{array}$$
Exercise. (a) Prove the proposition. (b) State and prove the cell version of this proposition.
The tangent bundle
What if we have a flow in space that varies from point to point? Then amount of flow through a cell will depend on the location of the cell.
To capture the possible directions of the flow, we associate a collection of cells, $St_a$, to every cell $a$ in $K$. It is the star of $a$, i.e., the set of all cell adjacent to $a$. The directions at $k$-cell $a\in K$ are given by the $(k+1)$-cells adjacent to $a$. Moreover, we can think of the $(k+1)$-chains as directions as long as each of them comes from the star of $a$. As defined previously, these directions are subject to algebraic operations on chains and, therefore, form a module, $T_a(K)$.
Thus, this is the setup for the whole complex.
- The space of locations is the set of all cells in the cell complex $K$.
- The space of directions is the set of all tangent spaces $T_a(K)$ at cells $a$ of $K$.
Definition. The total tangent space of $K$ is the disjoint union of the tangent spaces of all locations: $$\{T_aK\}:=\bigsqcup _{a\in K} \left( \{a\} \times T_a \right).$$
This space consists of (location, direction)-pairs: $$(a,\sigma)\in \{T_aK\},$$ where
- $a$ is a $(k-1)$-cell, and
- $\sigma$ is a $k$-cell.
Then the flow through a $(k-1)$-cell $a$ is a local $k$-form $\varphi_a$, different for each $a$: $$\varphi_a: T_a \to R.$$
Such forms are stitched together into a total form of degree $k$ over $K$ as a local $k$-form parametrized by location. It is a collection of linear functions, $$\varphi=\{\varphi_a:\ a\in K\}: \{T_aK\}\to R;$$ so that each of them, $$\varphi_a: \{a\} \times T_a \to R,$$ is a local $k$-form on $T_a$.
For the flow (as well as other applications, such as diffusion), the preservation of matter is satisfied:
- the amount of material that leaves location $A$ for location $B$ should be the same as the amount arriving to $B$ from $A$.
For the flow, $A$ and $B$ are two adjacent $k$-cells.
Definition. The equivalence relation of balance on the total tangent space $\{T_aK\}$ of a cell complex $K$ is given by: $$(a,\sigma)\sim (b,\tau) \text { if } i_a(\sigma)=i_b(\tau),$$ where $$i_a:T_a(K) \to C(K)$$ is induced by the inclusion of $St_a \hookrightarrow K$. Then the tangent bundle of $K$ is defined to be $$TK:=\{T_aK\}/ _\sim.$$
This equivalence reduces the size of the tangent space via the quotient construction:
The disconnected parts of $\{T_aK\}$, the tangent spaces, that come from the complex $K$, are glued back together.
Theorem. (1) The equivalence relation of balance preserves the operations on each tangent space. (2) The tangent bundle $$TK:=\{T_aK\}/_{\sim}$$ is a module. (3) $$TK=C(K).$$ (4) The restrictions of the identification map to the tangent spaces are monomorphisms: $$T_a(K)\to C(K).$$
Exercise. Prove the theorem.
Proposition. The $k$-forms preserve the equivalence relation and, therefore, are well defined as linear maps $\varphi : C(K) \to R$.