This site is being phased out.
Derivative as a limit
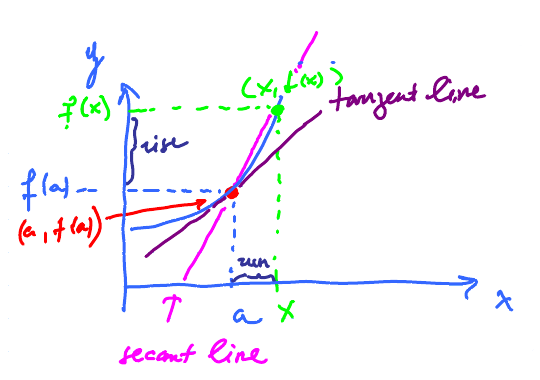
Derivative is the slope of the tangent line.
But what is the tangent line? (Silly answer: Line the slope of which is equal to the derivative).
What do we need it for? Recall the examples:
- Velocity
- Headlights
- Sling
i.e. it is used to study motion.
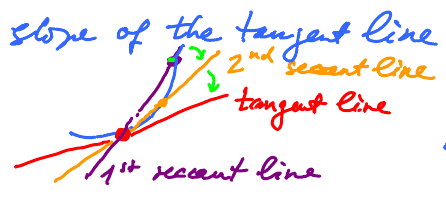
To find the tangent line, we only need its slope. We define its slope as the limit of slopes of the secant lines, lines determined by two points on the graph. For each $x \neq a$, draw a line through $(a,f(a))$ and $(x,f(x))$. We have infinitely many secant lines. Taske one: $$\text{Slope of this line } = \frac{\text{rise}}{\text{run}} = \frac{f(x) - f(a)}{x-a}$$ Then the slope of the tangent line $$\lim_{x \to a} \frac{f(x) - f(a)}{x-a}$$
So, as we move $x$ toward $a$, the secant lines turn and approach the tangent line, provided the limit exists. This number is called the derivative of $f$ at $x = a$. Note: this is not limit of $f$ but of the "difference quotient", a new function made from $f$.
Review exercise. Compute and justify: $$\lim_{x\to \infty} \frac{-x^{2} + 2x - 7}{2x^{2} + 77}$$
Example. Find the tangent line to $y = x^{2}$ at $(1,1)$.
Slope = the derivative of $y=x^{2}$ at $x=1$.
Use $f(x) = x^{2}$, $a =1$ in the definition. $$\begin{aligned} f^{\prime} &= \lim_{x \to a} \frac{f(x) - f(a)}{x - a} \\ & = \lim_{x \to 1} \frac{x^{2} - 1^{2}}{x - 1} \\ & = \lim_{x \to 1} \frac{(x-1)(x+1)}{x-1} \\ & = \lim_{x \to 1} ( x + 1 ) \\ & = 1 + 1 \\ &= 2 \quad \text{ Slope } \end{aligned}$$
The point-slope form of the line: $$ y - 1 = 2(x - 1)$$ Consider: $$f^{\prime}(a) = \lim_{x \to a} \frac{\overbrace{f(x) - f(a)}^{?}}{\underbrace{x - a}_{0}}$$ What are the limits of the numerator and the denominator? $$\lim_{x \to a} \underbrace{\left(f(x) - f(a)\right)}_{\text{If continuous, substitute}} = f(a) - f(a) = 0$$ This is an indeterminate expression. So, possibly the derivative exists.
What if $f$ is not continuous at $x = a$? Then $$\lim_{x \to a} \frac{\overbrace{f(x) - f(a)}^{\text{This limit does not exist.}}}{\underbrace{x - a}_{0}}$$ Then $f^{\prime}(a)$ does not exist.
Therefore...
Theorem. If $f$ is not continuous at $x = a$, then the derivative $f^{\prime}(a)$ does not exist.
We say that $f$ isn't differentiable.
Example. Consider $$f(x) = x^{2} \to f^{\prime}(1) = \lim_{x \to a} \frac{x^{2} - 1^{2}}{x-1}$$ To resolve $\frac{0}{0}$, we factor numerator. It's easy.
Factoring, in general, is hard...
Alternative definition of derivative
Rename $h = x - 1$. Then
$$f^{\prime}(a) = \lim_{x \to a} \frac{f(x) - f(a)}{\underbrace{x - a}_{h = x - a}}$$ Since $h = x - a$, then $x = a + h$
Rewrite the definition: $$ f^{\prime}(a) = \lim_{x \to a} \frac{f(a + h) - f(a)}{h} $$
This makes life easier...
Example. Given $$f(x) = x^{2}.$$
$$\begin{aligned} f^{\prime}(1) &= \lim_{h \to 0} \frac{f(1 + h) - f(1)}{h} \\ & = \lim_{h \to 0} \frac{(1 + h)^{2} - 1^{2}}{h} \\ & = \lim_{h \to 0} \frac{1^{2} + 2h + h - 1}{h} \\ & = \lim_{h \to 0} \frac{2h + h^{2}}{h} \qquad \frac{0}{0} \\ & = \lim_{h \to 0} (2 + h^{2}) = 2 + 0^{2} = 2 \end{aligned}$$
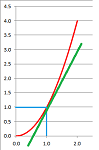
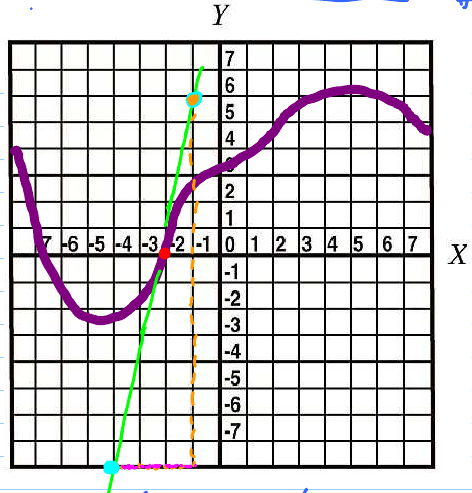
Problem. One can estimate the derivative from the graph. Let's find the derivative at the red point.
$$\text{Derivative } = \text{ Slope of the tangent line}$$
- Find it. It's the green line.
- Find its slope. $\frac{\text{Rise}}{\text{Run}} = \frac{14}{3} \approx 5$.
To better estimate the slope, draw a triangle as large as possible.
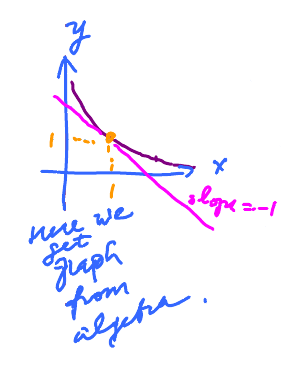
Here we get algebra from the graph. It's typically vice versa.
Find $f^{\prime}(1)$ for $f(x) = \frac{1}{x}$.
$$\begin{aligned} f^{\prime} &= \lim_{h \to 0} \frac{f(1 + h) - f(1)}{h} \qquad \to \frac{0}{0} \\ &= \lim_{h \to 0} \frac{\frac{1}{1+h} - \frac{1}{1}}{h} \qquad \to \frac{0}{0} \\ &= \lim_{h \to 0} \frac{\frac{1}{1+h} - \frac{1+h}{1+h}}{h} \\ &= \lim_{h \to 0} \frac{1 - (1-h)}{1+h} \cdot \frac{1}{h} \\ &= \lim_{h \to 0} \frac{-h}{1 + h}\cdot \frac{1}{h} \\ &= \lim_{h \to 0} -\frac{1}{1 + h} \\ &= -\frac{1}{1+0} = -1 \end{aligned}$$ This is a rational function, continuous on its domain. To evaluate the limit, plug in.
Example. Evaluate: $$\lim_{x \to 5} \frac{2^{x} - 32}{x - 5}. $$ It's just a limit. But we recognize that this is the derivative of some function. Compare to the definition $$ f^{\prime}(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} $$ and match.
So $$\begin{gathered} a = 5 \\ f(x) = 2^{x} \\ f(5) = 2^{5} = 32 \end{gathered}$$
So our limit, $f^{\prime}(5)$ for $f(x) = 2^{x}$. Compute: $$f^{\prime}(x) = (2^{x})^{\prime} = 2^{x} \ln 2, $$ so $$f^{\prime}(5) = 2^{5} \ln 2 = 32 \ln 2.$$