This site is being phased out.
Curvature
Problem. Can a car with a 10ft turning circle drive on a ramp of 8ft diameter? The answer depends on how tight is the turn of the ramp and it's not 8ft.
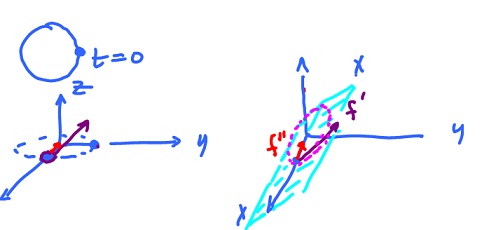
Let us first consider the circle as a parametric curve: $$g(t) = ( r \cos t / r, r \sin t / r )$$ with radius $r$. Then the tightness of the turn, the curvature, is the reciprocal of the radius: $$\kappa = 1 / r.$$
Definition. The curvature of the curve $z = g(t)$, where t is the natural parameter, at $f(t)$ is defined by $$\kappa = ‖ g' ' (t) ‖.$$
It's like the strength of the $g$-force that you have to deal with when turn...
Example. Circle: $$g'(t) = ( -\sin t / r, \cos t / r ),$$ $$g' '(t) = ( - 1 / r \cos t / r, - 1 / r \sin t / r ).$$ $$\kappa = ‖ g' '(t) ‖ = 1 / r ‖ ( \cos t / r, \sin t / r ) ‖ = 1 / r.$$
Example. Helix: $$g(t) = ( \cos t / √2, \sin t / √2, t / √2)$$ (natural parameter). Then $$g'(t) = ( -1 / √2 \sin t / √2, 1 / √2 \cos t / √2, 1 / √2)$$ $$g' '(t) = ( -1 / 2 \cos t / √2, -1 / 2 \sin t / √2, 0)$$ and $$\kappa = ‖ g' '(t) ‖ = 1 / 2 ‖ ( \cos t / √2, \sin t / √2 ) ‖ = 1 / 2.$$
We define the radius of curvature as $1 / \kappa$.
- Helix: $1 / \kappa = 2$, radius $= 1$
- Circle: $1 / \kappa = 1$, radius $= 1$.
The osculating circle approximates the curve at the point and has radius equal to $1 / \kappa$. This way the curvature of the circle is the same as that of the curve. The circle is located in the osculating plane determined by $g'$ and $g' '$, below.
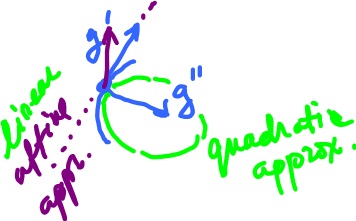
Compare:
- $y = mx + b$, the best affine approximation, linear polynomial;
- $ax^2 + bx + c$, quadratic polynomial.
How do we find the osculating circle? Consider
- $y=f(t)$ at $t = a$,
with $t$ the natural parameter. Compute $\kappa, R = 1 / χ$. The center of the circle is $$f(a) + R f' '(a) / ‖ f' '(a) ‖ = f(a) + 1 / \kappa^2 f' '(a).$$
Example. Let us consider a helix, $$a = 0, \kappa = 1 / 2, R = 2.$$
Here $$f(0) = ( 1, 0, 0 ),$$ $$f'(0) = ( 0, 1 / √2, 1 / √2),$$ $$f' '(0) = ( -1 / 2, 0, 0).$$
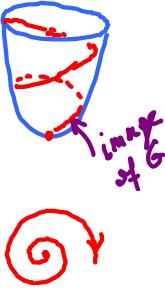
What if $t$ isn't natural? Then we can plot $$g(τ) → f( γ(τ) ),$$ and we know $γ$. Then the formula is $$\kappa = ( ‖f'‖ f' ' - < f', f' ' > f' ) / ‖f'‖^4 .$$
Example. Consider the curve $$G(s) = ( s \cos s, s \sin s, s^2 + 1 )$$ on the surface $$x^2 + y^2 = z - 1.$$ This is another way of representing the curve: $$x = s \cos s, y = s \sin s, z = s^2 + 1.$$ These $x, y, z$ have to satisfy the equation $$( s \cos s )^2 + ( s \sin s)^2 = ( s^2 + 1 ) - 1$$ or $$s^2 \cos^2 s + s^2 \sin^2 s = s^2.$$ Now one can see from the Pythagorean Theorem that the equation $$s^2 ( \cos^2 s + \sin^2 s) = s^2$$ holds.