This site is being phased out.
Convergence of the discrete to the continuous
Contents
Calculus vs. discrete calculus
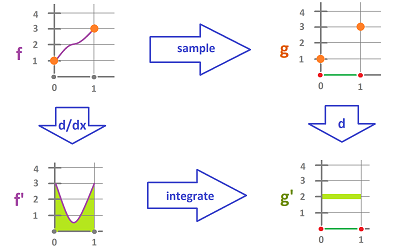
Calculus vs. discrete calculus? They have the same part and behave the same, so far. Indeed, this is how discrete calculus fits into the familiar calculus:
The diagram commutes. Indeed, given a function $f:{\bf R}\to {\bf R}$, we can proceed in two ways:
- right then down: we acquire a $0$-form $g$ by sampling function $f$, and then we acquire $dg$ by taking the differences of the values of $g$; or, alternatively,
- down then right: we acquire first the derivative $f'$ of $f$, and then we find the exterior derivative (a $1$-form) $dg$ by integrating $f'$ on the segments:
$$dg\Big([a,b] \Big):= \displaystyle\int_{[a,b]}f'dx.$$ The result is the same. Then we can say that calculus and discrete calculus develop in parallel.
But does the latter approximate the former? Will increasing the “resolution” of the discretization allow us to recover the original? What about convergence?
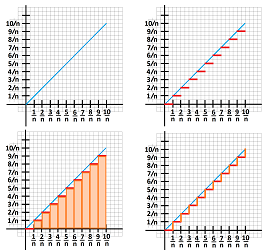
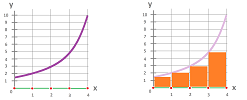
Example. Recall that the integrals of step-functions approximate the integral of a function, i.e.e, the area under its graph.
In contrast, an attempt to use the graphs of these functions to approximate the length of the graph fails, manifestly: $$\hspace{.29in}L:= \displaystyle\sum_{i=0}^{n-1} \Big( \tfrac{1}{n}+\tfrac{1}{n} \Big)=\tfrac{2}{n}\sum_{i=0}^{n-1} 1 =\tfrac{2}{n}n = 2.\hspace{.28in}$$
$\square$
Exercise. Use other step-functions to approximate the length of the diagonal segment.
Example. Let's use step-functions to approximate the area and the length of the circle:
Turns out that, in the digital world, $\pi =4$:
$\square$
We can find other examples when a discrete geometry fails to mimic its continuous counterpart.
Exercise. Show that this is the case of the diagonal spread of liquid not being quite diagonal:
Exercise. What about the pattern of heat transfer below?
These mismatches are examples of the frequent lack of convergence of the discrete to the continuous.
Convergence under discretizations
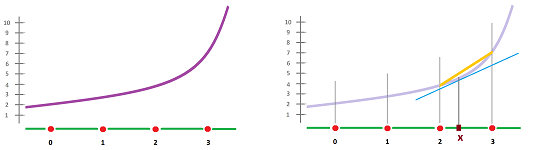
Suppose we have a function $f$ and a sequence of real-valued $0$-forms $g_k$. Then, what do we mean when we say that, as $k\to \infty$, $$g_k:{\mathbb R} \to {\bf R} \text{ converges to } f: {\bf R} \to {\bf R}?$$
Let's start with the simplest case. Suppose an integer $k=0,1,2,...$ is given. Every function $f:{\bf R}\to {\bf R}$ is discretized by sampling points, $$g_k(s):=f\left( \frac{s}{2^k} \right), \ s\in {\bf Z}.$$ This creates a real-valued $0$-form $g_k$ but each time it is defined on a different copy of ${\mathbb R}$. Let's consider the whole setup.
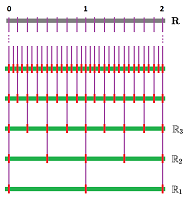
Suppose we have a sequence of copies of the standard cubical complex ${\mathbb R}$, $$\{ {\mathbb R}_k:\ k=0,1,2,3...\}.$$ Then, we need to align them as if by inclusion: $${\mathbb R}_0 \subset {\mathbb R}_1 \subset {\mathbb R}_2 \subset {\mathbb R}_3 \subset ... \subset {\bf R}.$$ For that, we define these maps: $$i_k (s):=2s,\ s\in {\bf Z}.$$ They generate the chain maps $$i_k:C({\mathbb R}_k) \to C({\mathbb R}_{k+1}),\ k=0,1,2....$$
We also define the sampling maps: $$I_k:{\mathbb R}_k \to {\bf R},\ k=0,1,2...,$$ by $$I_k(s)= \frac{s}{2^k},\ s\in {\bf Z}.$$ Then, $$I_{k+1}i_k=I_k.$$
We can also endow each ${\mathbb R}_k$ with a geometry such that the edges are smaller and smaller: $$|AB|=\frac{1}{2^k}.$$ In that case, the maps above are isometries.
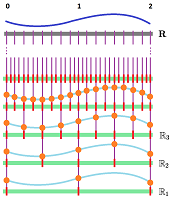
As $g_k$ are constructed from $f$ by sampling, the meaning of convergence is obvious:
The sequences are simply constant: for all $s\in {\bf Z}$ and for large enough $k$, we have $$g_k(s):=f(I_k(s))=f\left( \frac{s}{2^k} \right).$$
Next, what about convergence of the integrals?
We can use the outline in the last subsection. Then the approximations are, once again, “perfect”. Indeed, suppose we are given an interval $[A,B]\subset {\bf R}$ and suppose $f$ is integrable on $[A,B]$. Then, for every complex $K$ representing $[A,B]$ we define $g$ as the $1$-form acquired by integrating $f$ on the edges of $K$. Then, for any $1$-chain $q$ in $K$ with $\partial q=B-A$, we have $$ \int_A^Bf(x)dx = \int_q g.$$
If, instead, we sample the original function, the approximations are non-trivial but they do converge.
We rephrase the familiar result from calculus about left-end approximations of the Riemann integral.
Theorem. Suppose we are given an interval $[A,B]\subset {\bf R}$ and suppose $f$ is integrable on $[A,B]$. Then, for every $\varepsilon >0$ there is a $\delta >0$ such that if $K$ is a geometric complex $K$ with a realization $r:K\to [A,B]$ and $\operatorname{mesh}(K)<\delta$ and if $q$ is a $1$-chain in $K$ with $\partial q=B-A$, then $$\left| \int_A^Bf(x)dx - \int_q g \right|<\varepsilon,$$ where $g$ is the $1$-form acquired by sampling $f$ at the vertices of $K$: $$g\left( PQ \right):=f(r(P)),\ PQ\in K.$$
Exercise. Prove the theorem.
Next, what about convergence of the derivatives?
The convergence is point-wise but the values are intervals rather than points. For a given $s\in {\bf Z},\ n\in {\bf Z},n\ge 0$, we have as $i\to +\infty$: $$\begin{array}{llll} \frac{dg_{n+i}\Big( [s2^i,s2^i+1] \Big)}{2^{n+i}}&=\frac{g_{n+i}(s2^i+1)-g_{n+i}(s2^i)}{2^{n+i}}\\ &=\frac{f\left( \frac{s2^i+1}{2^{n+i}} \right)- f\left( \frac{s2^i}{2^{n+i}} \right)}{2^{n+i}}\\ &=\frac{f\left( \frac{s}{2^{n}} +\frac{1}{2^{n+i}} \right)- f\left( \frac{s}{2^{n}} \right)}{2^{n+i}} \\ &\to f'\left( \frac{s}{2^n} \right) \ \text{ as } n\to \infty. \end{array}$$
Exercise. Show that, in this case, all the values of the derivative $f'$ of $f$ are the limits of sequences of values of $g_k'$, under the assumption that $f$ is continuously differentiable.
Exercise. Provide a similar analysis for ${\mathbb R}_k$ with $|AB|=1/k$.
We rephrase a familiar result from calculus.
Theorem. Suppose $f$ is continuously differentiable on $(A,B)$. Then, for every $\varepsilon >0$ there is a $\delta >0$ such that if $K$ is a geometric complex $K$ with a realization $r:K\to {\mathbb R}$ and $\operatorname{mesh}(K)<\delta$ and $x\in r(PQ)\cap (A,B),\ PQ\in K$, then $$\left| f'(x) - h'( PQ ) \right|<\varepsilon,$$ where $h$ is the $1$-form acquired by sampling $f$ on the edges of $K$: $$h\left( PQ \right):=f(r(Q))-f(r(P)).$$
Exercise. Prove the theorem. Hint: use the Mean Value Theorem.
Exercise. Provide a similar analysis for a convergent sequence of functions, $f_n\to f$.
Euler's method for ODEs
Given a function $$F:{\bf R}\times {\bf R} \to {\bf R},$$ an ordinary differential equation (ODE) of order $1$ with right-hand side function $P$ is: $$y'(t) = F(t,y(t)).$$ where we have
- a differentiable function $y\in C^0({\bf R})$, and
- a time instant $t\in {\bf R}$.
If we can't find $y$ explicitly, we think of the differential equation as a formula by which the slope of the tangent line to the graph of $y$ can be computed at any point on the curve, once the location of that point is known.
We use this information to approximate $y$. We do that one initial condition at a time. So, we are looking for a way to approximate $y$ that satisfies $$y'(t) = F(t,y(t)),\ \forall t\in [A,B], \qquad y(A)=X.$$
Each approximation will be a $0$-form $f$ on a complex that represents $[A,B]$ that satisfies the same initial condition, $f(A)=X$. It is built as follows.
The starting point $$(t_0,f(t_0)):=(A,X)$$ is known; then, from the differential equation, the slope at that point can be computed (it is exactly the slope of the tangent line of $y$). We take a step along that tangent line up to the next point. We choose a value for the horizontal component of this step: $$h:=(B-A)/N,$$ where $N$ is the number of steps. Then, for $n=0,1,2,...,N-1$, we have $$t_{n+1} := t_n + nh,$$ and $$f(t_{n+1}):= f(t_n) + hF(t_n,f(t_n)).$$
We recognize then that we have a geometric complex representing $[A,B]$: $$K:=\{t_{n}:n=0,1,2,...,N\}\cup \{t_{n}t_{n+1}:n=0,1,2,...,N-1\},$$ with $|t_{n}t_{n+1}|=h$.
Furthermore, we have an ODE of cochains on $K$ that approximates the original: $$f'(PQ)=G(P,f(P)),$$ where the right-hand side function $$G:C_0(K)\times {\bf R} \to {\bf R}$$ is given by the same formula as $F$. Here, we have
- a cochain $f\in C^0(K)$,
- a node $P\in K$, and
- a edge $PQ\in K$.
On a finite interval, this approximate solution does not deviate too far from the original, unknown curve. Furthermore, the difference between the two curves can be made as small as we like by choosing the step size small enough. The general result is as follows.
Theorem. Suppose we are given an interval $[A,B]\subset {\bf R}$ and suppose $F$ has bounded partial derivatives on $[A,B]\times {\bf R}$. Suppose the initial position is given: $X\in {\bf R}$. Then, for every $\varepsilon >0$ there is a $\delta >0$ such that if $K$ is a geometric complex $K$ with a realization $r:K\to [A,B]$ and $\operatorname{mesh}(K)<\delta$, then $$\left| f(C) - y(r(C)) \right|<\varepsilon,\ \forall C\in K,$$ where
- $y$ is the solution of the IVP $y'(t) = F(t,y(t)),\ y(A)=X$, and
- $f$ is the solution of the IVP $f'(PQ)= F(r(P),f(P)),\ f(r^{-1}(A))=X$.
Exercise. Provide the analog of the above theorem for ODEs of chain maps $f:C(K)\to C({\mathbb R})$.
How do we measure the length of a curve in a digital image?
In order to understand the contents of an image, we need to be able to do some basic measurements of what is shown.
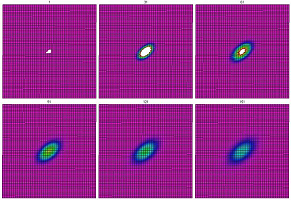
Example. Suppose we want to use computer vision to count nuts and bolts in an image:
Suppose we have detected and captured these objects. We can find their areas. However, since some of these objects have about the same size in terms of the area, we have to look at their shapes. We want to be able to evaluate shapes of objects and the most elementary way to do it is to compare their areas to their perimeters. The ability to compute lengths becomes crucial. $\square$
Specifically, we use roundness of objects, which is $$Roundness = 4\pi \frac{area}{perimeter^2}. $$ The roundness will tell circles from squares and squares from elongated rectangles. For example, a circle's roundness is $1$; while two rectangles may have the same area but a very different roundness:
In binary images (and cubical complexes, curves are represented as sequences of adjacent edges.
As we know, the length of the curve should be the total sum of distances between consecutive points. It is our concern however that the same “physical” curve will have different digital representations -- depending on the image's resolution and the curve's orientation with respect to the grid. For the length to be a meaningful characteristic of the "physical" curve, the representations should approximate the its length: as the resolution increases, the lengths of the digital representations should converge to the "true" length of the curve.
Exercise. Show that the area is independent of digital representation, in the above sense.
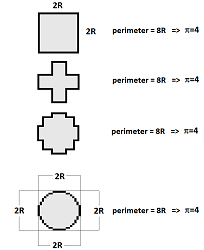
Example. Here is a simple example: the perimeters of a square and the inscribed circle are the same!
Indeed, it takes exactly as many vertical and horizontal steps to get from the left end of the circle to the top - no matter whether you make just one turn or many. The curve isn't really a curve... $\square$
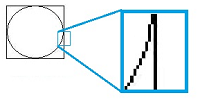
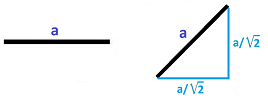
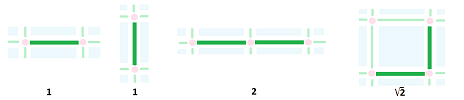
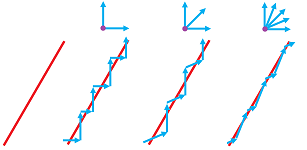
Example. Let's consider a simpler example in more detail. If $r$ is the size of the pixel, a line segment of length $a$ will be represented by, roughly, $a/r$ pixels... but only if it is placed horizontally or vertically!
If it is placed diagonally, there will be $\sqrt{2}a/r$ pixels arranged in the staircase pattern. Thus we have the following:
- Horizontal orientation: length $= a$;
- Diagonal orientation: length $= \sqrt{2}a \approx 1.42a.$
Conclusion: the length depends on the orientation of the curve with respect to the grid of the image. $\square$
The problem described here is also known as “Weyl's tile paradox” in physics.
Thus, the digital length of a curve may vary by $40\%$!
We may try to deal with this problem the same way one would deal with other accuracy problems -- by increasing the resolution of the image. In fact, a curve can be approximated by a digital curve with any degree of accuracy:
Unfortunately, the error is independent of the resolution.
Exercise. Show why.
Example. Ignoring the error may be dangerous. The roundness is supposed to be lower for elongated objects, like bolts. Let's consider again what was shown above.
- Diagonally oriented square with side a:
- area $= a^2$,
- perimeter $= 4\sqrt{2}a$.
- Horizontally oriented rectangle with sides $b=(\sqrt{2}-1)a$ and $b'=(\sqrt{2}+1)a=5b$:
- area $= a^2$,
- perimeter $= 4\sqrt{2}a$.
Thus, a horizontally oriented rectangle with proportions about $1$-to-$5$, just as in the image above, will have the same measurements as a diagonally oriented square. We can't tell a bolt from a nut... $\square$
Thus, approximations fail: even though computing the lengths of horizontal and vertical segments produces correct results, the lengths of diagonal segments are off by $40\%$.
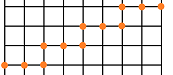
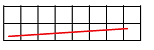
A possible remedy may be to break the curve into longer pieces. Every time we have a triple of consecutive points arranged in a triangle we should replace $1+1=2$ in the computation with $\sqrt{2}$. The result is that now, at least, all $45$ degree segments have correct lengths!
But what about $30$ degree segments? Consider segments with $2$ horizontal steps followed by $1$ vertical. Then
- “True” length $= \sqrt{2^2+1^2} = \sqrt{5} = 2.24. $
- Old method: length $= 3$.
- New method: length $= 1+\sqrt{2} = 2.41$.
The error is still almost $8\%$!
Exercise. If the relative error for the length is $n\%$, what is the relative error for the roundness?
Next we try an angle between $0$ and $30$ degrees, and so on:
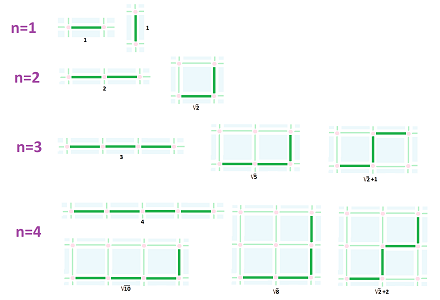
To sum up:
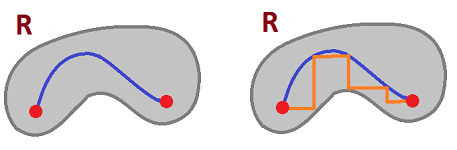
- one breaks a digital curve into a sequence of $n$-step curves,
- each curve is assigned a length (such as the distance from the beginning to the end), then
- the length of the original curve is the sum of those.
As the length of the edge approaches $0$, the length computed this way should converge to the “true” length. We prove that in general it does not:
An informal "explanation" is that once $n$ is chosen, the number of possible angles that curves of $n$ steps can generate is finite. Then, there are slopes that are missed and they cannot be approximated...
We use this idea to provide a simple proof of something tangible. Suppose there are only two available slopes, $a_1,a_2>0$. Let $b$ be their average: $$b:=\frac{a_1+a_2}{2}.$$ Let's compare
- the length the straight line from $(0,0)$ to $(1,b)$ with slope $b$, and
- the combined lengths of two straight lines from $(0,0)$ to $(1/2,a_1/2)$ with slope $a_1$, and from $(1/2,a_1/2)$ to $(1,b)$ with slope $a_2$.
The former is $$l:=\sqrt{1+b^2}.$$ The latter is $$L_0:=\sqrt{(1/2)^2+(a_1/2)^2}+\sqrt{(1/2)^2+(a_2/2)^2}.$$ Of course, $L_0>l$.
Theorem. Given $a_1,a_2$, there is such an $\epsilon >0$ that, if $L$ is the length of any line from $(0,0)$ to $(1,\frac{a_1+a_2}{2})$ that consists of segments of slopes $a_1$ and $a_2$, then $L/l>1+\epsilon$, where $l$ is the distance between these two points.
Exercise. Prove the theorem.
A more general about the relative errors of these approximations is as follows.
Corollary. Given $a_1,a_2,...,a_n>0$, there is such an $\epsilon >0$ and a number $b$ with $$\min a_i \le b\le \max a_i$$ that, if $L$ is the length of any line from $(0,0)$ to $(1,b)$ that consists of segments of slopes $a_1,a_2,..., a_n$, then $L/l>1+\epsilon$, where $l$ is the distance between these two points.
Exercise. Prove the corollary. Hint: assume that $a_1>a_2>...> a_n$.
The arc-length as a limit of cell approximations of a curve
It might seem counter-intuitive that the approximations fail to converge to the correct length.
In fact, one might recall from calculus that the arc-length of a curve is defined as the limit of approximations of the curve by line segments. The difference is that here the end-points of the segments lie exactly on the curve while in our construction they may be -- within a pixel -- off the curve. As a result, in the latter case all slopes are permissible while in the former only finitely many, as we have seen. This is why these combinations of segments do converge as functions (with respect to the sup-norm) but their derivatives don't! Considering that the derivative appears in the arc-length formula itself, we shouldn't be surprised to see that there is no convergence of the lengths without convergence of the derivatives, i.e., the slopes.
A calculus-free explanation is that the geometry of ${\bf R}^2$ (and the universe) is independent of direction, i.e., isotropic. Limiting ourselves to grids with fixed directions makes our approximation of this universe anisotropic. And making the grid finer and finer won't make it isotropic.
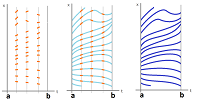
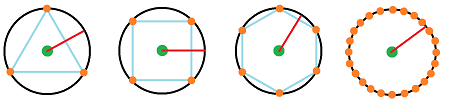
Indeed, let's take a look at these are possible angles from a few grids:
We can always find an angle that isn't there! Then the difference of the slopes of this line and the nearest grid line determines the relative error of the approximation of the length.
Conclusion: the approximation scheme we have used is invalid.
Solution: make the set of available angles in the approximations denser and denser.
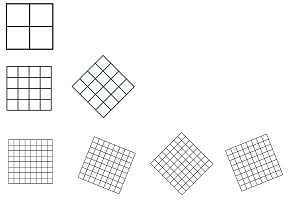
This is a way to do it: a sequence of square grids that alternates between
- shrinking of the squares and
- rotating the grids through smaller and smaller angles:
Specifically, we define $K_{nm}$ to be a copy of ${\mathbb R}^2$ that satisfies the following. For any $AB\in K_{nm}$ we have
- $|AB|=1/n$, and
- $AB$ is either parallel or perpendicular to the line $\pi/m$ from the $x$-axis.
Theorem. Suppose $\{K_{nm}\}$ is the sequence of cubical complexes defined above. Then, given a line segment $L$ between points $A$ and $B$ in ${\bf R}^2$, for any $\varepsilon >0$ there is an $N$ such that for any $n>N$ there is an $m$ and a $1$-chain $a_n$ in $K_{nm}$ such that $$\partial a_n=B_n-A_n,$$ where $A_n$ is in the star of $A$ and $B_n$ is in the star of $B$ in $K_{nm}$, and $$|a_n| < (1+ \varepsilon ) |L|.$$
Proof. For the sake of the proof we assume that it is the segment $L$ that is rotated:
For any $n$ there is an $m$ such that $$\sin \left(\alpha - \frac{m\pi}{n} \right)|L| < 1/n.$$ Now we simply choose $a_n$ to be the horizontal sequence of edges. Then, $$|a_n| < \cos \left(\alpha - \frac{m\pi}{n} \right)|L|.$$ $\blacksquare$
The problem we faced in the last subsection is resolved!
Now, what about actual curves?
Theorem. Suppose $\{K_{nm}\}$ is the sequence of cubical complexes defined above. Suppose also that $C$ is a rectifiable curve between points $A$ and $B$ in ${\bf R}^2$ with arc-length $|C|$. Then, for any $\varepsilon >0$ there is an $N$ such that for any $n>N$ there is an $m$ and a $1$-chain $a_n$ in $K_{nm}$ such that $$\partial a_n=B_n-A_n,$$ where $A_n$ is in the star of $A$ and $B_n$ is in the star of $B$ in $K_{nm}$, and $$|a_n| < (1+ \varepsilon ) |C|.$$
Proof. An outline... The curve is approximated by a sequence of segments just as in calculus. Then each segment is approximated by a $1$-chain according to the last theorem. $\blacksquare$
For the general setup, suppose $C$ is a rectifiable curve in ${\bf R}^n$ with arc-length $|C|$. To approximate it we follow the idea of the definition of the Riemann integral. Suppose we have
- $\gamma:=\{K\}$ is the set of all metric cell complexes each representing ${\bf R}^n$.
Furthermore, in each $K\in\gamma$, we approximate $L$ with a sequence of edges, i.e., a $1$-chain, $$L_K=a_1+...+a_m.$$ Then the length of this curve is the sum of the lengths of the edges, $$|L_K|=|a_1|+...+|a_m|.$$ Thus we have
- a collection of $1$-chains $L_K\in K\in\gamma$.
Exercise. When does this collection $\{ |L_K|: K\in\gamma \}$ “converge”, to $|L|$? Hint: define two meshes.
Exercise. Consider also:
- Delaunay triangulations;
- barycentric subdivisions;
- the averages of several rotated square grids;
- random grids.