This site is being phased out.
Calculus exercises: part III
Contents
Examples
Example. Consider $$f(x,y) = ( x^2 + ( y - 2 )^2 - y )^{\frac{1}{2}} + 1.$$
(a) Domain: $$x^2 + ( y - 2 )^2 - y \geq 0,$$ $$x^2 + ( y - 2 )^2 \geq 4,$$ i.e., the region with boundary: $$x^2 + ( y - 2 )^2 = 2^2.$$ This is the circle of radius $2$ with center at $(0, 2)$.
(b) Graph: $$f( 0, y ) = ( ( y - 2 )^2 - y )^{\frac{1}{2}} + 1 = z,$$ hence $$z = ( x^2 + ( y - 2 )^2 - y )^{\frac{1}{2}} + 1\ \Longrightarrow\ ( z - 1 )^2 = x^2 + ( y - 2 )^2.$$ Then with $x = 0$: $$( z - 1 )^2 = ( y - 2 )^2 \ \Longrightarrow\ z - 1 = \pm ( y - 2 ),$$ and with $y = 0$: $$( z - 1 )^2 = x^2 \ \Longrightarrow\ z - 1 = \pm x.$$ Then $z = y - 1$ and $z = -y + 3$ result in two lines. These cross-sections give us the graph.
(c) This is funnel, a truncated cone. $\square$
Example. To prove that $|| x ||$ is continuous, use $$|| x || = ( x_1^2 + ... + x_n^2 )^{\frac{1}{2}},$$ and show that $$|| x - a || < \delta \ \Longrightarrow\ \bigg| || x || - || a || \bigg| < \delta,$$ by the Triangle Inequality. $\square$
Example. Suppose $A$ and $B$ are path-connected and $a$ is in the intersection. If $P$ and $Q$ belong to the union, find a path from $P$ to $a$, from $a$ to $Q$. This gives you a path from $P$ to $Q$. $\square$
Example. Show that $$T(x) = x_2^2 + 2x_2 + 1$$ is the best linear approximation of the function $$f(x) = x_1^4 + x_2^2.$$ Consider $$\begin{array}{} \displaystyle\lim_{x \to a} \frac{f(x) - T(x)}{|| x - a ||} &= \displaystyle\lim_{x \to (0,-1)} \frac{x_1^4 + x_2^2 + 2x_2 + 1}{|| ( x_1, x_2) - ( 0, -1)||} \\ &= \displaystyle\lim_{x \to (0,-1)} \frac{x_1^4 + x_2^2 + 2x_2 + 1}{( ( x_1 - 0 )^2 + ( x_2 + 1 )^2)^\frac{1}{2}} \\ &= \displaystyle\lim_{x_2 \to (-1)} \frac{x_2^2 + 2x_2 + 1}{| x_2 + 1 |} \\ &= \displaystyle\lim_{x_2 \to -1} \frac{(x_2 + 1 )^2}{| x_2 + 1 |} &\text{ by canceling } ( x_2 + 1 ) \\ &= \displaystyle\lim_{x_2 \to -1} | x_2 + 1 | \\ &= 0. \end{array}$$ $\square$
Example. Let $$h(t) = ( \sin e^t, \cos e^t).$$ Then $h$ is the composition of
- $f: {\bf R} \to {\bf R}$ given by $f(t) = e^t$, and
- $g: {\bf R} \to {\bf R}^2, g(x) = ( \sin x, \cos x)$.
Then $$f'(t) = e^t, {\nabla}g = (\cos x, -\sin x),$$ and by the Chain Rule, $$h' = ( g {\circ}f )' = {\nabla}g \cdot f' = ( \cos e^t, -\sin e^t ) e^t.$$ $\square$
Example. Describe the curve which results from the vector valued function $$r(t) = ( \cos 2t, \sin 2t, t ),$$ where $t \in {\bf R}$.
Solution: The first two components indicate that for $$r(t) = ( x(t), y(t), z(t) ),$$ the pair $( x(t), y(t) )$ traces out a circle. While it is doing so, $z(t)$ is moving at a steady rate in the positive direction. Therefore, the curve which results is a cork screw shape, i.e. a helix. $\square$
Example. The position of a particle at time $t$ is $( x, y )$, where $$x = \sin \ t,$$ $$y = \sin^2 t.$$ Describe the motion of the particle as t varies over the time interval $[ a, b ]$.
Solution: We can eliminate $t$ to see that the motion of the object takes place on the parabola $y = x^2$. The orientation of the curve is from $( \sin a, \sin^2 a )$ to $( \sin b, \sin^2 b)$. $\square$
Example. Find the limit $$\displaystyle\lim_{x \to 1} \frac{x^2 - x}{x - 1}.$$
Solution: It is $$\frac{x \cdot ( x - 1 )}{x - 1} = x {\rm \hspace{3pt} for \hspace{3pt}} x \neq 1.$$ Hence $$\displaystyle\lim_{x \to 1} \frac{x \cdot ( x - 1 )}{x - 1} = \displaystyle\lim_{x \to 1} x = 1.$$ $\square$
Example. Find the limit $$\displaystyle\lim_{x \to \infty} \frac{x}{1 + x}.$$
Solution: Rewrite $$\frac{x}{1 + x} = \frac{1}{1 + \frac{1}{x}}.$$ Now it is $$\displaystyle\lim_{x \to \infty} \frac{1}{1 + x} = 1 \neq 0.$$ Therefore, $$\displaystyle\lim_{x \to \infty} \frac{x}{1 + x} = \displaystyle\lim_{x \to \infty} \frac{1}{1 + \frac{1}{x}} = \frac{1}{1} = 1.$$ $\square$
Example. Consider $f: {\bf R} \to {\bf R}^3$. Is $$f( t ) = ( t^2 + 1, \cos( 2t ),\sin( 3t) )$$ continuous?
Solution: All components are continuous for all $t \in {\bf R}$, so $f(t)$ is continuous on ${\bf R}$. $\square$
Example. Let $f: {\bf R} \to {\bf R}^2$. Is $$f( t ) = ( ( t + 1 )^{\frac{1}{2}}, \tan( t ) )$$ continuous?
Solution: The first component is defined and continuous for $$t \geq -1, $$ while the second component is defined and continuous for $$t \neq \frac{\pi}{2} + k {\pi}, k \in {\bf Z}.$$ Hence it is continuous on ${\bf R}$ for $$t \geq -1 \text{ and }t \neq \frac{\pi}{2} + k {\pi}, k \in {\bf Z}.$$ $\square$
Example. Let $f: {\bf R} \to {\bf R}^3$, $$f( t ) = \left( \frac{1}{t^2 - 1}, ( 1 - t^2)^{\frac{1}{2}}, \frac{1}{t} \right).$$ If $f$ continuous?
Solution: The first component is defined and continuous for $$t \neq \pm 1.$$ The second component is defined and continuous for $$t \in [ -1, 1 ],$$ while the third component is defined and continuous for $$t \neq 0.$$ Hence, $f$ is continuous on ${\bf R}$ for $$t \in ( -1, 0 ) \cup ( 0, 1 ).$$ $\square$
Example. Let $g: {\bf R} \to {\bf R}^4$, $$g( t ) = ( \cos(4t), 1 - ( 3t + 1 )^{\frac{1}{2}}, \sin(5t), \sec(t) ).$$ If $g$ continuous?
Solution: The first and the third component are continuous on ${\bf R}$. The second component is continuous and defined on $( -\frac{1}{3}, \infty )$, while the secant $\sec(t) = \frac{1}{\cos(t)}$ in the fourth component is defined and continuous for $$t \neq \frac{\pi}{2} + k\pi, k \in {\bf Z}.$$ Hence, $g(t)$ is continuous as long as $$t \geq -\frac{1}{3} \text{ and }t \neq \frac{\pi}{2} + l{\pi},\ l \in {\bf Z}.$$ $\square$
Example. Let $$f( t ) = ( \sin \ t, t^2, t + 1 ) \text{ for } t \in [ 0, 5 ].$$ Find a tangent line to the curve parametrized by $f$ at the point $t=2$.
Solution: A direction vector has the same direction as $f'(2)$. Therefore, it suffices to simply use $f'(2)$ as a direction vector for the line. Further, $$f'(2) = ( \cos \ 2, 4, 1 ).$$ Hence, a parametrized equation for the tangent line is $$( x, y, z ) = ( \sin \ 2, 4, 3) + t ( \cos \ 2, 4, 1).$$ $\square$
Example. Let $$f( t ) = ( \sin t, t^2, t + 1 ) \text{ for } t \in [ 0, 5 ].$$ Find the velocity vector for $t = 1$.
Solution: The velocity vector is simply $f'(1) = ( \cos 1, 2, 1 )$. $\square$
Example. Consider $g: {\bf R} \to {\bf R}^2$, $$g( t ) = ( t, t^2 ).$$ What is its velocity, speed and acceleration as it passes through $( 2, 4 )$?
Solution: It is $$g'( t ) = ( 1, 2t )$$ and $$g' '( t ) = ( 0, 2 ).$$ Further, at $( 2, 4 )$, we know $t = 2$. For the velocity at $t = 2$, we have $g'(2) = ( 1, 4 )$. The speed equals $$|| g'(2) || = ( 1^2 + 4^2 )^{\frac{1}{2}} = \sqrt{17},$$ whereas the acceleration is equal to $g' '(2) = ( 0, 2 )$. $\square$
Example. An object has position $$r(t) = ( t^3, \frac{t}{1 + t}, ( t^2 + 2 )^{\frac{1}{2}} )\ km .$$ where $t$ is given in hours. Find the velocity of the object in kilometers per hour when $t = 1$.
Solution: Since velocity at time t equals $r'(t)$, we calculate $$\begin{array}{} r'(t) &= \left( 3t^2, \frac{1 ( 1 + t ) - t}{( 1 + t )^2}, 2t \cdot \frac{1}{2} ( t^2 + 2 )^{-\frac{1}{2}} \right) \\ &= \left( 3t^2, \frac{1}{( 1 + t )^2}, \frac{1}{( t^2 + 2 )^{\frac{1}{2}}} t \right). \end{array}$$ For $t = 1$, the velocity is $$r'(1) = \left( 3, \frac{1}{4}, \frac{1}{\sqrt{3}} \right) km / hour.$$ $\square$
Example. Consider $g: {\bf R} \to {\bf R}^2$, $$g(t) = ( \frac{1}{t}, 2t )$$ defined on $( 0, \infty )$. Its image is one branch of a hyperbola (this can be seen by writing $g(t) = ( x, y )$, i.e. $x = \frac{1}{t}, y = 2t$, which yields $y = \frac{2}{x})$. Find the velocity, the speed and the acceleration at time $t$.
Solution. The velocity equals $$g'(t) = ( -\frac{1}{t^2}, 2 ),$$ the acceleration is equal to $$g' '(t) = ( \frac{2}{t^3}, 0 ),$$ and the speed is $$|| g'(t) || = || ( -\frac{1}{t^2}, 2 ) || = ( \frac{1}{t^4} + 4 )^{\frac{1}{2}}.$$ $\square$
Example. For the function $$f( t ) = ( 3t \cos( 2t ), 4t \sin\}( 2t ) ),$$ calculate $f'(t)$.
Solution: Apply the product rule for both components: $$f'(t) = ( 3 \cos( 2t ) - 6t \sin ( 2t ), 4\sin( 2t ) + 8t \cos ( 2t ) ).$$ $\square$
Example. For the function $$f( t ) = ( 3t \cos( 2t ), 4t \sin( 2t ) ),$$ show that $$\frac{d}{dt} || f(t) || \neq || f'(t) || .$$
Solution: It is $$\begin{array}{} || f(t) || &= ( 9t^2 \cos^2(2t) + 16t^2 \sin^2(2t) )^{\frac{1}{2}} &= ( 9t^2 + 7t^2 \sin\}^2(2t) )^{\frac{1}{2}}, \end{array}$$ and its derivative equals $$\frac{d}{dt} || f(t) || = \frac{9t + 14t^2 \sin(2t) \cos(2t) + 7t \sin^2(2t)}{9t^2 + 7t^2 \sin^2(2t) )^{\frac{1}{2}}}.$$ Further $$f'(t)= ( 3\cos(2t) - 6t \sin(2t), 4\sin(2t) + 8t \cos(2t) ),$$ and thus $$\begin{array}{lll} || f'(t) || &= ( ( 3 \cos(2t) - 6t \sin(2t) )^2 + (4 \sin(2t) + 8t \cos(2t))^2 )^{\frac{1}{2}} \\ &= ( 9 + 7 \sin^2(2t) + 36 t^2 + 28 t^2 \cos^2(2t) + 14t \sin(4t) )^{\frac{1}{2}}. \end{array}$$ Now evaluating both functions at $t = {\pi}$ (for example) yields $$(\frac{d}{dt} || f(t) ||)_{t= \pi} = \frac{9 \pi}{ \sqrt{9 \pi ^2}} = 3,$$ whereas $$|| f'( \pi ) || = \sqrt{9 + 64{\pi}^2} \approx 25.31,$$ hence $\frac{d}{dt} || f(t) || \neq || f'(t) ||$. $\square$
Example. Let $$r(t) = ( t^2, \sin t, \cos t )$$ and let $$p(t) = ( t, \ln( t + 1 ), 2t ).$$ Find $( r(t) \times p(t) )'$.
Solution: From the cross-product rule, it is $$( r(t) \times p(t) )' = ( 2t, \cos t, -\sin t) \times ( t, \ln( t + 1 ), 2t ) + ( t^2, \sin t, \cos \ t ) \times ( 1, \frac{1}{t + 1}, 2 ).$$ $\square$
Example. Let $$F = yi - xj + 2k = < y, -x, 2 >$$ be a vector field. Verify that the path $$g(t) = ( \sin t, \cos t, 2t )$$ is a flow line (i.e. a path such that the velocity along the path is a vector in the vector field, $g'(t) = F(g(t)) )$ for the vector field $F$.
Solution: With $$( x, y, z ) = ( \sin t, \cos t, 2t )$$ it follows that $$g'(t) = ( \cos t, -\sin t, 2 ),$$ and $$F(g(t)) = ( y, -x, 2t ) = ( \cos t, -\sin t, 2t ).$$ $\square$
Example. Consider the path $g: {\bf R} \to {\bf R}^2$, $$g(t) = ( \cos^3 t, \sin^3 t ),$$ which describes an astroid. For $t \in [ 0, \frac{\pi}{2} ]$, one fourth of the astroid is described. Calculate its arc-length.
Solution: With $$g'(t) = ( -3 \sin t \cos^2 t, 3 \sin^2t\cos t ),$$ $$|| g'(t) || = 3 \sin t \cos t = \frac{3}{2} sin 2t,$$ it is $$\begin{array}{} \displaystyle\int_0^{\frac{\pi}{2}} || g'(t) ||\, dt &= \displaystyle\int_0^{\frac{\pi}{2}} \frac{3}{2}\sin 2t\, dt \\ &= -\frac{3}{4} \cos\}(2t) |_0^{\frac{\pi}{2}} \\ &= -\frac{3}{4} \cos \pi + \frac{3}{4}\cos 0 = \frac{3}{2}. \end{array}$$ $\square$
Example. Consider the path $f: {\bf R} \to {\bf R}^2$, $$f(t) = ( t^2, \frac{2}{3} ( 2t + 1 )^{\frac{3}{2}} ), 0 \leq t \leq 4.$$ Calculate its arc-length.
Solution: It is $$\begin{array}{} \displaystyle\int_0^4 || f'(t) || dt &= \displaystyle\int_0^4 ( 4t^2 + 4( 2t + 1 ) )^{\frac{1}{2}} dt &= \displaystyle\int_0^4 2( t + 1 ) dt &= t^2 + 2t |_0^4 &= 24. \end{array}$$ $\square$
Example. Find the arc-length of the helix $$g(t) = ( \cos t, \sin t, t )$$ from $t = 0$ to $t = 2{\pi}$.
Solution: The arc-length equals $$\begin{array}{} \displaystyle\int_0^{2 \pi} || g'(t) || dt &= \displaystyle\int_0^{2 \pi} ( -(\sin t)^2 + \cos^2 t + 1 )^{\frac{1}{2}}\, dt \\ &= \displaystyle\int_0^{2 \pi} ( \sin^2 t + \cos^2 t + 1 )^{\frac{1}{2}} dt \\ &= \displaystyle\int_0^{2 \pi} \sqrt{2} dt \\ &= \sqrt{2} (2{\pi} - 0 ) \\ &= 2 \sqrt{2}{\pi}. \end{array}$$ $\square$
Example. Parametrize the helix $$g(t) = ( \cos t, \sin t, t )$$ for $t \in [0,2{\pi}]$ by arc-length.
Solution: It is $$\begin{array}{} \displaystyle\int_0^t || g'(t) || dt = \displaystyle\int_0^t \sqrt{2} dt = \sqrt{2} t \end{array}$$ for all $t \in [0,2{\pi}]$. We can solve for $t$ in terms of $s$: $$t = \alpha(s) = \frac{s}{\sqrt{2}},$$ and hence $$g(s) = \left( \cos \frac{s}{\sqrt{2}}, \sin \frac{s}{\sqrt{2}}, \frac{s}{\sqrt{2}} \right)$$ for all $s \in [0,2 \sqrt{2}{\pi}]$. $\square$
Example. Find the arc-length of the curve whose cylindrical coordinates are given by $$r = e^t,$$ $$\theta = t,$$ $$z = e^t$$ for $t \in [0,1]$.
Solution: With $$r'(t) = e^t,\ \theta '(t) = 1,\ z'(t) = e^t,$$ we obtain $$\begin{array}{} \displaystyle\int_0^1 ( r'(t)^2 + r(t)^2 \theta'(t)^2 + z'(t)^2)^{\frac{1}{2}}\, dt &=\displaystyle\int_0^1 ( e^{2t} + e^{2t} (1) + e^{2t} )^{\frac{1}{2}}\, dt \\ &= \displaystyle\int_0^1 e^t \sqrt{3}\, dt \\ &= \sqrt{3} (e - 1). \end{array}$$ $\square$
Example. Interpretation of the gradient. Consider a room in which the temperature is given by a scalar field $T$, so that at each point $(x,y,z)$ the temperature equals $T(x,y,z),$ assuming the temperature does not change in time. How can the gradient be interpreted?
Solution: In this case, at each point in the room, the gradient of $T$ at that point will show the direction in which the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction. $\square$
Example. Interpretation of the gradient. Consider a hill whose height above sea level at a point $(x,y)$ is $H(x,y)$. How can the gradient of $H$ be interpreted?
Solution: The gradient of $H$ at a point is a vector pointing in the direction of the steepest slope at that point. The steepness of the slope at that point is given by the magnitude of the gradient vector. $\square$
Example. Consider a room in which the temperature is given by $$f(x,y,z) = x y^2 z^3.$$ Consider further that a fly is crawling at unit speed in the direction of the vector $$v = < -1, 1, 0 >$$ starting at the point $$s = ( 2, 1, 1 ).$$ Compute that rate of temperature change the fly is about to experience.
Solution: It is $${\nabla}f(x,y,z) = < y^2 z^3, 2xyz^3, 3xy^2z^2 >,$$ hence $${\nabla}f(2,1,1) = < 1, 4, 6>.$$ Further, $$\frac{v}{|| v ||} = < -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0 >,$$ and thus $$\frac{df}{ds} = < 1, 4, 6> \cdot <-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0 > = \frac{3}{\sqrt{2}}.$$ $\square$
Example. Let $f: {\bf R}^3 \to {\bf R}$, $$f(x,y,z) = x + \sin(xy) + z.$$ Find the directional derivative $D_v f(1,0,1)$, where $$v = < \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} >.$$
Solution: Note that $v$ is already a unit vector. Therefore, it is only necessary to find ${\nabla}f(1,0,1)$ and take the dot product. It is $${\nabla}f(x,y,z) = ( 2x + \cos(xy) y, \cos(xy) x, 1),$$ and hence $${\nabla}f(1,0,1) = ( 2, 1, 1 ).$$ The directional derivative is obtained as $$<2,1,1> \cdot < \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} > = \frac{4}{3} \sqrt{3}.$$ $\square$
Example. Let $f: {\bf R}^3 \to {\bf R}$. Find the equation of the tangent plane to the level surface $f(x,y,z) = 6$ of the function $$f(x,y,z) = x^2 + 2y^2 + 3z^2$$ at the point $( 1, 1, 1 )$.
Solution: First note that $(1,1,1)$ is a point on the level surface (i.e. $f(1,1,1) = 6$ ). To find the desired plane it suffices to find the normal vector to the proposed plane. But we see $${\nabla}f(x,y,z) = < 2x, 4y, 6z >,$$ and hence $${\nabla}f(1,1,1) = < 2, 4, 6 >.$$ Therefore, the equation of the tangent plane is: $$< 2, 4, 6> + ( x - 1, y - 1, z - 1 ) = 0,$$ or $$2x + 4y + 6z - 12 = 0.$$ $\square$
Example. Compute the gradient of the function $$f(x,y) = x^2 \sin(xy) $$ at $( {\pi}, 0 )$.
Solution: It is $${\nabla}f({\pi},0) = \left[ \begin{array}{} f_x({\pi},0) \\ f_y({\pi},0) \end{array} \right] = \left[ \begin{array}{c} 2x \sin(xy) + x^2 y \cos(xy) \\ x^3 \cos(xy) \end{array} \right]_{(\pi, 0)} = <0, \pi^3>.$$ $\square$
Algebra and geometry
- Set up, but do not solve, a system of linear equations for the following problem: “Suppose your portfolio is worth $\$ 1,000,000$ and it consists of two stocks $A$ and $B$. The stocks are priced as follows: $A$ $\$2.1$ per share, $B$ $\$1.5$ per share. Suppose also that you have twice as much of stock $A$ than $B$. How much of each do you have?”
- Give the number $t$ that makes $X=<3,2,1>$ and $Y=<2,t,t>$ perpendicular.
- Here are $xyz$-equations for two planes: $x+y-z=0$ and $x-y+z=0$. Explain how you can tell that these planes cut each other NOT at right angles.
- A plane has an $xyz$-equation $x+y=2$. Give a vector perpendicular to the plane.
- In an effort to find the line in which the planes $ 2x -y- z=2 $ and $-4x+2y+2z=1$ intersect, a student multiplied the first one by $2$ and then added the result to the second. He got $0=5$. Explain the result.
- Determine whether these points lie on a straight line: $A=(0,-5,5),\ B=(1,-2,4),\ C=(3,4,2)$.
- Find the plane through the point $P=(-1,6,-5)$ and parallel to the vectors $A=<1,1,0>$ and $B=<0,1,1>.$
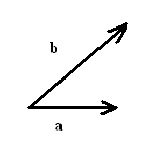
- Vectors $A$ and $B$ are given below. Copy the picture and illustrate graphically (a) $A+B$, (b) $A-B$, (c) $||A||$, (d) the projection of $A$ on $B$, (e) the projection of $B$ on $A$.
- Find the angle between the vectors $<1,1,1>$ and the $x$-axis. Don't simplify.
- Find the plane through the origin perpendicular to the line from $(1,0,0)$ and $(0,1,1)$.
- Find an equation of the plane through $(2,1,0)$ and parallel to $x+4y-3z=1$.
- (a) Find the angle between the planes $x+y+z=1$ and $x-2y+3z=1$. (b) Find the equation of the line of intersection of these planes.
- Find the vector equation of the line parallel to both $xy$- and $xz$- coordinate planes an passing through $(2,3,1)$.
- Solve the system of linear equations:
$$\left\{\begin{array}{lll} x&-y&=-1,\\ 2x&+y&=0.\\ \end{array}\right. $$
- Find the reduced row echelon form of the following system of linear equations. What kind of set is its solution set?
$$\left\{\begin{array}{lll} -x&-2y&+z&=0,\\ 3x&&+z&=2,\\ x&-y&+z&=1. \end{array}\right.$$
- Represent the system of linear equations as a matrix equation:
$$\left\{\begin{array}{lll} x&-y&+z&=-1,\\ 3x&&+z&=2,\\ 2x&+y&+z&=1. \end{array}\right.$$
- Represent this matrix equation as a system of linear equations:
$$\left[ \begin{array}{lll} 1 & 3 & 2\\ 0 & 2 & 0\\ -1 & 0 & 3 \end{array} \right] \left[\begin{array}{lll} x\\ y\\ z \end{array} \right] =\left[\begin{array}{lll} 1\\ 2\\ 3 \end{array} \right]. $$
- Give explicitly the solution set of the system of linear equations represented by its augmented matrix:
$$\left[\begin{array}{lll|l} 1&0&2&-1\\ 0&1&1&2\\ \end{array}\right].$$
- Find scalars $a$ and $b$ such that $a<1,2>+b<−1,3>=<1,7>$.
- Is it possible for a system of linear equations to have: (a) no solutions, (b) exactly one solution, (c) exactly two solutions, (d) infinitely many solutions? Give an example or explain why it's not possible.
- Find the set of all vectors in ${\bf R}^2$ that are orthogonal to $<-1,3>$. Write the set in the standard form of a line through the origin.
- Compute:
$$\left[ \begin{array}{lll} 1 & 3 & 2\\ 0 & 2 & 0\\ -1 & 0 & 3 \end{array} \right] \left[\begin{array}{lll} 1\\ 0\\ 2 \end{array} \right] . $$
Parametric curves
- Suppose $h(t)=(\sin e^t,\cos e^t)$ is a parametric curve. (a) What is its path? (b) Show how the Chain Rule is used to compute its derivative.
- Suppose you are towing a trailer-home. During the first few minutes, every time you look at the rear view mirror you can see only the lower part of the home. Later, every time you look you can see only the top part. Discuss the profile of the road.
- Suppose during the first $2$ seconds of its flight an object progressed from point $(0,0)$ to $(1,0)$ to $(1,1)$. What was its (a) average velocity, (b) average acceleration?
- Sketch the following parametric curve:
- $x(t)=\frac{1}{t}, y(t)=\sin t,\ t>0$;
- $< x, y > = < \cos t, 2 >$;
- $r=2^ti+2^{2t}j$;
- $x=1/t,y=1/t^{2},\ t>0$.
- Find all points on the curve $x=t\cos t,\ y=t\sin t,\ t>0,$ where the tangent vector points in the following direction: 1. up, 2. left, 3. down, 4. right.
- Suppose a ball in thrown horizontally at speed $v$ feet per second by a person $h$ feet tall. Represent the motion as a parametric curve in the $3$-dimensional space.
- Sketch the parametric curve
$$x=\frac{1}{t}\cos t,\ y=\frac{1}{t}\sin t,\ t>0.$$
- Suppose an object is dropped from a 100 feet building. You are standing 100 feet away from the building and tracing the object with a laser. Express the angle of the laser as a function of time.
- At time $t$ with $0 \leq t$, an object is at the position $$P(t)=\bigg( t^2 +1,\frac{1}{t+1},e^{2t}\bigg) .$$ Calculate its velocity, $V(t)$, and its acceleration, $A(t)$, as functions of $t$.
- Parametrically describe the line segment with endpoints $(-1,-1,-1)$ and $(1,1,1)$.
- “If $f$ is continuous at $x_{0}$ then $\lim_{x\to x_{0}}\frac{f(x)}{e^{x}}$ exists.” True or false? Explain.
- Find a parametric curve such that $F'(t)=(e^{t},\sin t)$ and $F(0)=(0,1)$.
- Show that for any parametric curve $\lim_{t\to t_{0}}\frac{1}{t}F(t)=0$ implies $\lim_{t\to t_0}F(t)=0$.
- Let $X=F(t)$ be a differentiable parametric curve. If $F'(t)$ is perpendicular to $F(t)$ for all $t$, show that $||F(t)||$ is constant.
- (1) Sketch the parametric curve $x=\cos t,\ y=\sin 2t$. (2) The curve intersects itself. Find the angle of this intersection.
- If the velocity of an object at time $t$ is given by $V(t)=<1+t^2,\sqrt{t}>$, what is its position at time $t=3$ if the objects starts at the origin?
- Find the unit tangent vector of the curve $$F(t)=ti+tj+(1+t^{2})k$$ at the point $(0,0,1)$.
- Plot and describe the curve
$$x(t)=|\sin t|,\ y(t)=|\cos t|,\ z=t.$$
- Find the line tangent to the curve $$F(t)=(t^{5},t^{4},t^{3})$$ at point $(1,1,1)$.
- Find the unit normal vector of the curve
$$G(t)=3ti+2t^{2}j.$$
- Find the curvature of the curve $<t,t^{2}>$.
- Find the equation of the line tangent to the curve $$x=t^{5},\ y=t^{4},\ z=t^{3},$$ at the point $(1,1,1).$
- Sketch the following parametric curve: $$x=|\cos t|,\ y=|\sin t|,\ -\infty <t <+\infty.$$ Describe the curve and the motion.
- Find the line tangent to the curve $F(t)=<t^{5},t^{4},t^{3}>$ at the point $(1,1,1)$.
- Suppose a ball in thrown horizontally at speed $w$ feet per second by a person $h$ feet tall. At what speed will the ball hit the ground?
- Give the definition of the curvature. Give examples of curves with various curvatures.
- Find all points on the curve $x=3\cos t,\ y=2\sin t$ where the tangent vector points in the following direction: (a) up, (b) left, (c) down, (d) right.
- Sketch a curve on the plane the curvature of which is: (a) increasing, (b) decreasing, (c) constant non-zero, (d) zero.
- Sketch the following parametric curve: $$x=t^3,\ y=t^5,\ -1\le t \le 1.$$ Is this a regular parametrization?
- (a) Give the definition of the curvature (as a certain derivative). (b) Use the definition to compute the curvature of a circle of radius $R$.
- Find the line tangent to the curve $$r(t)=<t^{5},t^{4},t^{3}>$$ at the point $(1,1,1)$.
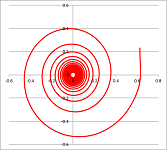
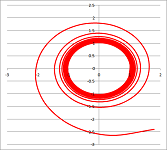
- Find an equation of the spiral in space converging to the origin as below (view from above):
- An artillery gun with a muzzle velocity of $1000\ ft/s$ is located atop a seaside cliff $500$ ft high. At what initial inclination angle should it fire a projectile in order to hit a ship at sea $20,000$ ft from the foot of the cliff? Assume $g=32\ ft/s^{2}.$
- Find the center of curvature of the parabola $y=x^{2}$ at the point $(1,1)$.
- Find the arc-length of the curve $x=2e^{t}$, $y=e^{-t}$, $z=2t$, from $t=0$ to $t=1$.
- Describe and sketch the parametric curve $f(t)=(t^3-t,1-t^2)$.
- Represent as a parametric curve with domain $(- \infty, \infty)$ a plan spiral approaching $0$ but never reaching it.
- Find the tangent line to the curve $f(t)=(t,t^2,t^3)$ at the point $(1,1,1)$.
- Show that the parametrization of the curve $f(t)=(3\sin t,4\cos t)$ isn't natural. Find the equation for the natural parameter. Do not solve.
- Find the function $f: {\bf R} \rightarrow {\bf R}^2$ such that $f' '(t)=(\cos t, \sin 3t)$ and $f(0)=(1,0), f'(0)=(0,0)$.
- Let $f(t)=(t^3-3t,t^2)$. (a) Find the derivative $f'$ of $f$. (b) Use $f'$ to plot the parametric curve $f$.
- Use the arc-length formula to compute the length of the circle of radius $3$ centered at $(1,1)$.
- (a) Find the natural parametrization of the helix $F(t)=(\cos t, \sin t,t)$. (b) Find its curvature. (c) Find the center of the osculating circle at $(1,0,0)$.
- The curve $(t^3-t,t^2-1)$ has a self-intersection at $0$. Compute the angle.
- Here are parametric equations for two lines: $(x,y,z)=(1+2t,3t,2+5t)$ and $(x,y,z)=(-1,-1,-1)+t(1,0,1)$. Say how you can tell that these lines are NOT parallel.
Functions of several variables
- Show that the limit doesn't exist:
$$\lim_{(x,y)\to (0,0)}\frac{xy}{x^{2}+y^{2}}.$$
- Plot a few points of the graph of the function $h(x,y)=3-x-2y$ to demonstrate that this is a plane.
- Find the best linear approximation of the function $f(x,y)=xy^2$ at the point $(0,1)$.
- Find the linearization of the function $f(x,y)=e^{xy}$ at $(0,1)$.
- Find the directional derivative of the function $f(x,y)=2x^2-3y$ at the point $(1,1)$ in the direction of the vector $<1,0>$.
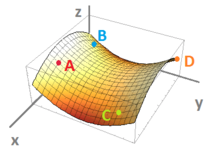
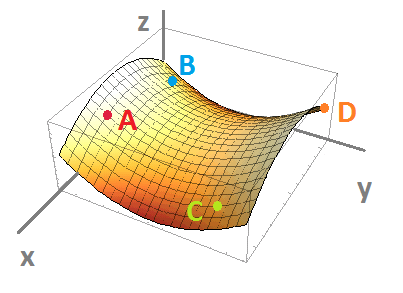
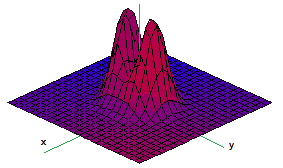
- Sketch the contour (level) curves of the function shown below, along with points $A,B,C,D$, on the $xy$-plane:
- Find the equation of the tangent plane to the surface $z=\sqrt {4-x^{2}-2y^{2}}$ at the point $(1,-1,1).$
- Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.
- Find the directional derivative of the function $f(x,y)=x/(y+z)$ at the point $(4,1,1)$ in the direction of the vector $v=<0,2,-1>$.
- Find the maximum rate of change of the function $f(x,y)=\sin (xy)$ at the point $(1,0)$ and the direction in which it occurs.
- Find $\frac{dw}{dt},$ where
$$w=xy+yz^{2},\ x=e^{t},\ y=e^{t}\sin t,\ z=e^{t}\cos t.$$
- Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs:
$$f_x>0,\ f_{xx}>0,\ f_y<0,\ f_{yy}<0.$$
- The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Sketch the gradient for each on a separate $xy$-plane:
- Make a sketch of contour (level) curves for the following function.
- Draw the contour map (level curves) of the following function of two variables:
- $g(x,y)=\ln(x+y)$;
- $f(u,v)=uv$;
- $h(x,y)=2x-3y+7$;
- $z=x^2+y^2$.
- Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs:
$$\begin{array}{c|ccccccccc} & 1&2&3&4\\ \hline f_x &+&+&-&+\\ f_{xx}&-&+&+&-\\ f_y &-&-&+&+\\ f_{yy}&-&+&-&+ \end{array}$$
- The graph of a function of two variables $z=f(x,y)$ is given below along with a point on the graph: 1. A, 2. B, 3. C, 4. D. Determine the signs of the derivatives $f_x,\ f_{xx},\ f_y,\ f_{yy}$ at that point:
- Find the partial derivatives of the following function of three variables:
- $g(x,y,z)=z\sqrt{x+y}$;
- $u=1$;
- $w=e^{x+y+z}$;
- $f(u,v,w)=uv+e^w$.
- Find the best linear approximation of the function $f(x,y)=xe^{y}$ at the following point: 1. $(0,0)$, 2. $(0,1)$, 3. $(1,1)$, 4. $(1,0)$.
- From the definition, find the directional derivative of the function $f(x,y)=2x-3y$ at the point $(1,1)$ in the direction of the following vector: 1. $<3,0>$, 2. $-2{\bf j}$, 3. $<1,1>$, 4. $<-1,-1>$.
- Find the partial derivatives of the function
$$f(x,y)=\dfrac{x}{y}+\sin(xy)+xe^{2y}.$$
- Find the equation of the tangent plane to the surface $z=y\cos(x-y)$ at the point $(2,2,2).$
- Set up as a max/min problem, but do not solve, the following: “Find the dimensions of a rectangular box of maximal volume such that the sum of lengths of its edges is equal to 10”.
- State the chain rule, for the case of the composition of a function of two variables and a function of one variable.
- Find the linearization of the function $f(x,y)=e^{xy}$ at $(0,1)$.
- Find all critical points of the function $f(x,y)=2x^3z-6x+z^2-2y+7$.
- Find the gradient of the function $f(x,y)=x^2y^{-3}$ at the point $(1,1)$. Use this information to sketch the graph of $f$ in the vicinity of this point. Explain.
- The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Provide the signs of the partial derivatives of $f$ at these points. For example, $\frac{\partial f}{\partial x}<0$ at point $A$.
- A function of two variables is given by $f(x,y)=xy^2$. (a) Find the linear approximation of $f$ around the point $(1,1)$. (b) Represent the graph of $f$ as a parametric surface and find the plane tangent to this surface at the point $(1,1,1)$.
- State the chain rule, for the case of the composition of a function of two variables and a function of one variable.
- The contour (level) curves for a function are given below. They are equally spaced. Sketch a possible graph that produced it and describe it.
- Represent the function $h(x,y)= \sqrt{x^2y-1}$ as the composition of two functions. Find its derivatives using the Chain Rule.
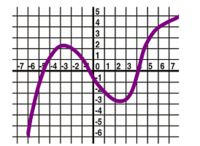
- The graph of function $y=g(x)$ of one variable is shown below. Suppose now that $z=f(x,y)=g(x)$ is a function of two variables, which depends only on $x$, given by the same formula. Find all points where the gradient of $f$ is equal to $0$.
- Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.
- Find the directional derivative of the function $f(x,y)=2x^2-3y$ at the point $(1,1)$ in the direction of the vector $<1,0>$.
- Represent the function $h(x,y)= \sqrt{x^2y-1}$ as the composition of two functions. Find its derivatives using the Chain Rule.
- Find the partial derivatives of the following function of three variables:
- $g(x,y,z)=z\sqrt{x+y}$;
- $u=1$;
- $w=e^{x+y+z}$;
- $f(u,v,w)=uv+e^w$.
- Find the best linear approximation of the function $f(x,y)=xe^{y}$ at the following point: 1. $(0,0)$, 2. $(0,1)$, 3. $(1,1)$, 4. $(1,0)$.
- From the definition, find the directional derivative of the function $f(x,y)=2x-3y$ at the point $(1,1)$ in the direction of the following vector: 1. $<3,0>$, 2. $-2j$, 3. $<1,1>$, 4. $<-1,-1>$.
- A function of two variables is given by $f(x,y)=xy^2$. (a) Find the linear approximation of $f$ around the point $(1,1)$. (b) Represent the graph of $f$ as a parametric surface and find the plane tangent to this surface at the point $(1,1,1)$.
- Find the best linear approximation of the function $f(x,y)=xy^2$ at the point $(0,1)$.
- Find the maximum rate of change of the function $f(x,y)=\sin(xy)$ at the point $(1,0)$ and the direction in which it occurs.
- Find an equation of the tangent plane to the surface $z=4x^{2}-y^{2}+2y$ at the point $(-1,2,4).$
- Find the directional derivative of the function $f(x,y)=1+2x\sqrt{y}$ at the point $(3,4)$ in the direction of the vector $<4,-1>$.
- Make a sketch of contour (level) curves for the function below:
- Find the dimensions of a rectangular box of maximal volume such that the total surface area is equal to $64$.
- A plane has an $xyz$-equation $2(x-1)+3(y-2)+4(z-3)=0$. Give a vector PARALLEL to the plane.
- Calculate the gradient $grad\, f(x,y,z)$ of $f(x,y,z)=xyz+ \frac{x}{y}$.
- Does $f(x,y)=-x^2e^{x^2+y^2}$ have a maximmu or minimum? How do you know?
- Calculate $\frac{\partial f}{\partial z}$ for $f(x,y,z)=e^{xyz}+x$ at the point $(1,2,3)$.
- You are at the point $(0,0)$. In the direction of what vector should you step off $(0,0)$ in order to get the greatest initial increase in the function $f(x,y)=x^2+\frac{1}{4}y^2$. Explain.
- Let $f(x,y)=\sin (x-y)$. Give a formula for the function $h(x)$ defined by $$h(x)=\displaystyle\int_0^{x}f(s,y)\,ds. $$
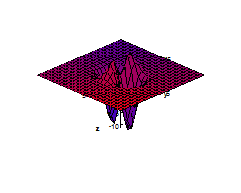
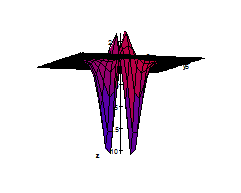
- Let $$f(x,y)= \sqrt{x^2+(y-2)^2-4}+1.$$
- a. Find the domain of $f$.
- b. Sketch the graph of $f$.
- c. What is it?
- Give an example of a function $z=f(x,y)$ such that $\frac{\partial f}{\partial x}(0,0)$ exists but $\frac{\partial f}{\partial y}(0,0)$ does not.
- From the definition, compute the directional derivative of the function $$f(x,y)=xy+y^2$$ at the point $a=(2,1)$ in the direction $v=(1,1)$.
- From the definition, prove that $T(x)=-2x_2-1$ is the best affine approximation of the function $$f(x)=x_1^4+x_2^2,$$ where $x=(x_1,x_2)$, at the point $a=(0,-1)$.
- Represent the function $$f(t)=(\sin e^{t},\cos e^{t})$$ as the composition of two functions and then use the Chain Rule to compute its derivative at $t_0=0$.
- Find all critical points of the function $$f(x,y,z)=xz+5y^2.$$
- Find and classify the critical points of the function $f(x,y)=x^{4}+y^{4}-4xy+1$.
- Find the tangent plane to the surface $f(x,y)=\sin (x-y)$ at $(\frac{\pi}{2},0,1)$.
- Give an example of a function of two variables such that:
- a. its image is the circle $x^2+y^2=1$,
- b. its image is the sphere $x^2+y^2+z^2=1$,
- c. its graph is the sphere $x^2+y^2+z^2=1$,
- d. its domain is the disk $x^2+y^2 \leq 1$,
- e. it is equal to its best affine approximation.
- Find the best affine approximation of the function $$f(x)=x_1^2+x_2^2+x_3^2,$$ where $x=(x_1,x_2,x_3)$, at the point $a=(0,-1,1)$.
- Find the global minima of the function $$f(x,y,z)=x^2z^2+y^2+y.$$
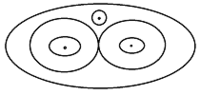
- A mountain ridge has three peaks with two passes between them. Sketch the level curves of the function that represents the terrain.
- Define the gradient of a function. What does it tell us about the function?
Integrals
- Estimate the integral $$\displaystyle\iint_{B}x^2y\,dA,$$ where $B=\{(x,y):0\leq x \leq 2,0 \leq y \leq 3\}$, by providing a Riemann sum with $6$ squares.
- Use a Riemann sum with $8$ terms to estimate the value of the integral $$\iiint_{D}(x+y+z)\, dV,$$ over the cube $D=[0,1]\times[0,1]\times[0,1]$. Choose your own sample points.
- Let $f:\mathbf{R}\to \mathbf{R}$ be a function such that $\int_{a}^{b}f(x)\, dx=1$. Let $B=\{(x,y):\ a\leq x\leq b,\ c\leq y\leq d\}$ be a rectangle. Find $\iint_{B}f\, dA$.
- Find the volume of the region bounded by the surface $z=1-x^{2}$, the $xy$-plane and the planes $y=0$ and $y=1$.
- Find the volume of the solid under the plane $x+2y-z=0$ and above the region bounded by $y=x$ and $y=x^{4}$.
- Find the area of the part of the surface $z=1+3x+2y^{2}$ that lies above the triangle with vertices $(0,0),\ (0,1),$ and $(2,1)$.
- Use a Riemann sum with $m=n=2$ to estimate the value of the integral $$\iint_{D}\sin(x+y)\, dA,$$ where $R=[0,\pi]\times [0,\pi]$. Choose your own sample points.
- Find the mass of the lamina that occupies the region $D$ bounded by $y=e^{x},\ $y=0,$\ x=0,\ x=1$, and its density function is $\rho(x,y)=y.$
- Express the length of the circle of radius $r$ as an arc length integral and evaluate it.
- Evaluate the iterated integral
$$\int\limits_{0}^{1}\int\limits_{0}^{z}\int\limits_{0}^{y} ze^{-y^{2}}\, dxdydz.$$
- Compute this integral below where region $D$ is bounded by: $y=0,\ y=x^2,\ x=1,\ z=0,\ z=2$:
$$\iiint_D(y+z)\, dV.$$
- Find the volume of the solid under the plane $x+2y-z=0$ and above the region bounded by $y=x$ and $y=x^{4}$.
- Find the area of that part of the plane $z=1+2x+2y$ that lies directly above the region in the $xy$-plane bounded by the parabolas $y=x^2-1$ and $y=-x^2+1$.
- Find the area of the part of the surface $z=1+3x+2y^{2}$ that lies above the triangle with vertices $(0,0),\ (0,1),$ and $(2,1).$
- Evaluate $$\iiint_{D}2x\, dV,$$ where
$$D=\{(x,y,z):0\leq y\leq2,\ 0\leq x\leq\sqrt{4-y^{2}},\ 0\leq z\leq y\}.$$
- Evaluate the double integral $\iint_{D}(x+y)\, dA,$ where $D$ is bounded by $y=\sqrt{x}$ and $y=x^{2}$.
- Define the double integral of a function of two variables over a rectangle. Make a sketch and explain.
- Find the volume of the tetrahedron bounded by the planes $x+2y+z=2,\ x=2y,\ x=0,$ and $z=0$.
- Define the double integral of a function of two variables over a rectangle. Make a sketch and explain.
- Find the volume of the tetrahedron bounded by the planes $x+2y+z=2,\ x=2y,\ x=0,$ and $z=0.$
- Compute this integral $$\iiint_D(y+z)\, dV,$$ where region $D$ is bounded by: $y=0,y=x^2,x=1,z=0,z=2$.
- You are faced with a hand calculation of $$\displaystyle\iint_{R}f(x)dxdy, $$ where $R$ is the two-dimensional region consisting of everything bounded by the curves $y=x^2,y=x^2+1$ and the lines $x=0,x=1$. Switch to new, convenient for integration, coordinates $u,v$ by indicating what $u,v$ are in terms of $x,y$ and describe $R$ in terms of $u,v$.
- By hand calculation, evaluate $$\displaystyle\iint_{R}1dxdy,$$ where $R$ is given in $u,v$ coordinates as $0 \leq u \leq 1,1 \leq v \leq 3$, and $x=u^2,y=v+u^2$.
- You are faced with a hand calculation of $$\displaystyle\iiint_{R}f(x,y,z)\,dxdydz,$$ where $R$ is the 3D region bounded from above by the unit sphere and from below by the $xy$-plane. Describe $R$ in a way convenient for integration.
- You are faced with a hand calculation of $$\displaystyle\iiint_{R}f(x,y,z)\,dxdydz,$$ where $R$ is the 3D region consisting of everything bounded by the planes $y=x,y=x+1,y=-x+1,y=-x+2,z=0,z=2$. Switch to new, convenient for integration, coordinates $u,v,w$ by indicating what $u,v,w$ are in terms of $x,y,z$ and describe $R$ in terms of $u,v,w$.
- Find the volume conversion factor of the transformation
$$x(u,v,w)=u^2v,\ y(u,v,w)=v^2,\ z(u,v,w)=w^2e^{u}.$$
- You are faced with a hand calculation of $$\displaystyle\iint_{R}f(x,y)\, dxdy,$$ where $R$ is the two-dimensional region consisting of everything bounded by the curves $y=x^2,y=x^2+2$ and the lines $x+y=1,x+y=2$. (a) Sketch $R$ in $xy$-plane. (b) Switch to new, convenient for integration, coordinates $u,v$ by indicating what $u,v$ are in terms of $x,y$. (c) Sketch $R$ in $uv$-plane.
- By hand calculation, evaluate $$\displaystyle\iint_{R}2dxdy, $$ where $R$ is given in $u,v$ coordinates as $1 \leq u \leq 2,0 \leq v \leq 1$, and $x=u^2+2v,y=ue^{v}$.
- You are faced with a hand calculation of $$\displaystyle\iiint_{R}f(x,y,z)\,dxdydz,$$ where $R$ is the "ice-cream cone", i.e., the 3D region obtained by intersecting the cone $z^2=x^2+y^2,z \geq 0$, and the sphere $x^2+y^2+z^2=2$. Describe $R$ in a way convenient for integration.
- Find the volume conversion factor of the transformation
$$x(u,v,w)=u^2+v+1,\ y(u,v,w)=v^2+w+2,\ z(u,v,w)=w^2+u+3.$$
- Find by integration the area of that part of the plane $2x+3y+z=6$ that lies in the first octant.
- Find the volume of the solid in $\mathbf{R}^{3}$ bounded by the following surfaces: $z=x^{2}+y^{2},$ $z=0,$ $y=x^{2}$, $y=2x$.
- By means of an appropriate change of variables, evaluate the integral $\int_{D}xy\,dA,$ where $D\subset \mathbf{R}^{2}$ is bounded by the lines $x=0$, $x=1$, $y=x$, $y=x+1$.
- Find the volume of a sphere of radius $a$.
- Find the volume of the region bounded by the surfaces $z=y$, $y=4$, $z=0$, $y=x^{2}$.
- Evaluate the integral $$\displaystyle\iiint_{B}\,xyz\,dV,$$ where $B=\{(x,y):0\leq x \leq 1,0 \leq y \leq 1,0 \leq z \leq 1 \}.$
- By using only the properties of the integral, compute $\displaystyle\iint_{D}f(x,y)\,dA$, where $D$ is the disk $x^2+y^2\leq 4$ and $f(x,y)=2$ if $-2 \leq x \leq 0$, $f(x,y)=-1$ if $0 \leq x \leq 2$, $f(x,y)=55$ for all other values of $(x,y)$.
- By using polar coordinates, compute the volume of the solid bounded by the cylinder $x^2+y^2=1$ and the planes $z=0$ and $z=1$.
- Compute the volume of the solid lying above the rectangle $R$ in the $xy$-plane consisting of all points $(x,y,0)$ with $-1 \leq x \leq 1,0 \leq y \leq 1$ and bounded from above by the surface given by $z=x^2y$.
Vector fields
- Sketch the vector field given below and estimate its line integral along the boundary of the square oriented counterclockwise (multiple answers are possible):
$$\begin{array}{llll} F(0,0)=<1,1>,& F(.5,0)=<0,1>,& F(1,0)=<1,1>,& F(1,.5)=<-1,1>,\\ F(1,1)=<-1,0>,& F(.5,1)=<0,0>,& F(0,1)=<2,1>,& F(0,.5)=<-1,-1>. \end{array}$$
- In the formula of Green's Theorem shown below, identify all of its parts (such as "$F$ is..."):
$$\oint_C F\cdot dP=\iint_D (q_x-p_y)\, dA.$$
- Sketch the velocity vector field $F(x,y)=<x,-y>$ identifying the most important features. Describe the motion in detail.
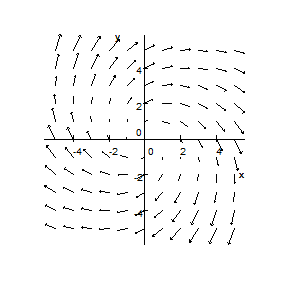
- State the path-independence property. Does the vector field shown below satisfy the path-independence property? Explain.
- (1) Represent the circle of radius $1$ centered at $0$ as a parametric curve. (2) Find the tangent line to this circle at the point $(\sqrt{2}/2,\sqrt{2}/2)$. (3) Compute the flux of the vector field $F=< 2,1 >$ across the part of the circle that lies in the first quadrant.
- Find the work done by force field $$V(x,y)=< xy,y^{2}>,$$ in moving an object along the parabola $x=t,\ y=t^{2},\ 0\leq t\leq1.$
- Vector field $V$ is sketched below. (a) Suppose $C$ is the positively oriented curve following the upper half of the unit circle. Is $$\int _{C}V\cdot dR$$ positive, negative or $0$? Explain. (b) Suppose $P=(4,4)$. Is $\operatorname{div} V(P)$ positive, negative or 0? Explain.
- Evaluate the line integral $$\int_{C}x^{2}y^{3}\, dx-y\sqrt{x}\, dy,$$ where $C$ is parametrized by $x=t^{2},\ y=-t^{3},\ 0\leq t\leq1.$
- (a) Explain what it means for a line integral $\int_{C}V\cdot dR$ to be independent of path. (b) Is $\int_{C}V\cdot dR,$ where $$V=<1-ye^{-x},e^{-x}>$$ independent of path?
- (a) State Green's Theorem. (b) Verify it for the vector field $$V(x,y)=yi-xj$$ and a unit square.
- This is the formula of Green's Theorem: $$\oint_{C} V\cdot dR = \iint_{D} \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\, dA. $$ Explain its parts and relations between them. Provide a sketch.
- Determine whether the vector field $V(x,y,z)=e^{z}i +j+xe^{t}k$ is conservative.
- Sketch the vector field $$V(x,y)=\dfrac{1}{\sqrt{x^{2}+y^{2}}}(yi-xj).$$
- Find the work done by force field $$V(x,y)=xyi+y^{2}j$$ in moving an object along the parabola $x=t,\ y=t^{2},\ 0\leq t\leq1.$
- (a) Given a vector field $V(x,y)=<3+2xy,x^{2}-3y^{2}>,$ find a function $f$ such that $\nabla f=V.$ (b) Use (a) to evaluate the line integral $\int_{C}V\cdot dR,$ where $C$ is the curve given by $$R(t)=<e^{t}\sin t,e^{t}\cos t>,\ 0<t<\pi.$$
- Verify Green's Theorem for the vector field $$V(x,y)=(x-y)i+xj$$ and the region $D$ bounded by the unit circle $$C:R(t)=\cos ti+\sin tj,\ 0\leq t\leq2\pi.$$
- Sketch the vector field $$\frac{1}{x^2+y^2}<x,y>.$$
- A vector field $V$ is sketched below. Suppose $C$ is the clockwise oriented square centered at the origin. Is $\int _{C}V\cdot dR$ positive, negative or $0$? Explain.
- Prove that the vector field $V(x,y,z)=zj - yk$ is not conservative.
- Sketch the vector field
$$V(x,y)=\dfrac{1}{x^{2}+y^{2}}(yi-xj).$$
- (1) Represent the cylinder of radius $1$ and height $1$ centered on the $z$-axis as a parametric surface. (2) Find the tangent plane to the cylinder at the point $(\sqrt{2}/2,\sqrt{2}/2,1/2)$. (3) Compute the flux of the vector field $F=< 2,1,1 >$ across the part of the cylinder that lies in the first octant.
- A vector field $V$ is sketched below. Suppose $C$ is the clockwise oriented square centered at the origin. Is $\int _{C}V\cdot dR$ positive, negative or $0$? Explain.
- Prove that the vector field $V(x,y,z)=zj - yk$ is not conservative.
- Sketch the vector field
$$V(x,y)=\dfrac{1}{x^{2}+y^{2}}(yi-xj).$$
- Find the work done by force field $$V(x,y)=< xy,y^{2}>$$ in moving an object along the parabola $x=t,y=t^{2},0\leq t\leq1.$
- Given vector field $F(x,y)=\left( x,\frac{1}{2}y \right)$. Choose a few points on the plane and draw the vector $F(x,y)$ with tail at $(x,y)$. There are a few families of trajectories in this vector field. Pencil in a few trajectories of each type.
- Suppose that a mass $M$ is fixed at the origin in space. When a particle of unit mass is placed at the point $(x,y)$ other than the origin, it is subjected to a force $G(x,y)$ of gravitational attraction. Plot the vector field $G(x,y)$, if the magnitude (length) of $G(x,y)$ is $\frac{kM}{r^2}$, where $r=\sqrt{x^2+y^2}$.
- Here is a plot of a few trajectories (and vectors) of a vector field. On the basis of the plot, determine if it is a gradient field or not. Explain.
- Use Gauss's formula to evaluate the flow of the vector field $F(x,y,z)=<z^2,y,x^2>$ across the surface of the pyramid bounded by the coordinate planes and the first octant part of the plane with equation $x+y+z=1$.
- Use Gauss's formula to evaluate the flow of the vector field $F(x,y,z)=<z+y,x+y,z>$ across the surface of the 3D box with a slanted top consisting of all points $(x,y,z)$ with $0 \leq x \leq 1,0 \leq y \leq 1,0 \leq z \leq x+1$.
- Find the divergence and the rotation of the vector field $F(x,y)=<x^2y,xy\sin y>$.
- Measure the flow of the vector field $G(x,y)=<e^{x}+y,e^{y}>$ ALONG the boundary of the rectangle with corners at $(0,0),(1,0),(0,1),(1,1)$.
- Suppose a closed curve is located within the unit circle. Is the flow of $H(x,y)=<\frac{x^3}{3}-2x,\frac{y^3}{3}>$ ACROSS this curve negative or positive? Explain.
- Find the best linear approximation of $F(x,y)=(xy,x^{2}+y^{2})$ at the point where $x=1$ and $y=1$.
- Find the best linear approximation of the function $F(x,y,z)=(xz+y,x^{2}+zy^{2})$ at the point where $x=1$, $y=1$, and $z=0$.
- Evaluate $\int_{C}(y^{2}+2xy)\,dx+(x^{2}+2xy)\,dy$. where $C$ is the part of the graph $y=2x^{2}$ from $(0,0)$ to $(1,2)$.
- Let $F(x,y)=\left(\dfrac{-y}{x^{2}+y^{2}},\dfrac{x}{x^{2}+y^{2}}\right)$ be a vector field, and let $C$ a simple (i.e., without self-intersections) closed path that encloses the origin. Find the work of $F$ along $C$. Hint: it is equal to the work along a certain circle.
Alternative coordinate systems
- Plot the curve $r=2\cos (3\theta )$. For 5 extra points, find the line(s) through the origin tangent to the curve.
- (a) Plot these points in polar coordinates: $(r,\theta )=(0,1),\ (1,0),\ (1,\pi),\ (2,3\pi)$. (b) Sketch these three polar curves: $r=1,\ \theta=0,\ r=\theta$.
- Find a polar representation of a curve similar to the one below, a spiral wrapping around a circle. What about one that is wrapping from the inside? (no proof necessary):
- Indicate if the following statements are true or false:
- In polar coordinates, $(1,\pi/2)$ and $(-1,-\pi/2)$ represent the same point.
- The curve $r=3+\cos \theta$ passes through the origin.
- The curve $r=\cos 2\theta$ is closed.
- The curve $r=1+\cos \theta$ is bounded.
- The graph of $r=\theta^2$ can be represented as a parametric curve in Cartesian coordinates.
- In polar coordinates, $A=(1,\pi/2)$ and $B=(-1,-\pi/2)$ represent the same point.
- The slope of the polar curve $r=0$ is equal to $0$.
- The graph of the curve $r=\cos 2\theta$ is a spiral.
- The parametric curve $x=t^2,\ y=\sin t$ is bounded.
- The graph of $r=\theta^2$ can be represented as a parametric curve in Cartesian coordinates.