This site is being phased out.
Calculus exercises: part II
Contents
Examples
Example. Find $\sqrt{4.01}$ with accuracy at least $.001$. We are to approximate with Taylor polynomials the function $f(x)=x^{1/2}$ around the point $a=4$.
First, we consider the constant approximation $T_0$ which produces the value of $\sqrt{4}=2$ as a substitute for $\sqrt{4.01}$. We compute: $$f'(x)=\frac{1}{2}x^{-1/2}.$$ We estimate this function on the interval $[4,4.01]$. Find $K_1$ such that $$\frac{1}{2}x^{-1/2}\le K_1$$ for all $x$ in $[4,4.01]$. Since $f'$ is decreasing, its maximum is at $x=4$ with the max value $f'(4)=\frac{1}{4}$. This the best estimate and we choose this number as $K_1$. Therefore, we consider $T_0$ with the error estimate: $$E_0=|T_0(x)-f(x)|\le K_1\frac{|x-4|}{1!}=\frac{1}{4}|x-4|.$$ Specifically, for $x=4.01$, we have: $$E_0\le \frac{1}{4}|4.01-4|=\frac{.01}{4}=.0025.$$ Not good enough!
We proceed to the linear approximation $T_1$. We compute: $$f' '(x)=\left(\frac{1}{2}x^{-1/2}\right)'=-\frac{1}{4x^{3/2}}.$$ We find $K_2$ from the estimate we need: $$\frac{1}{4x^{3/2}}\le K_2$$ for all $x$ in $[4,4.01]$. Since $f' '$ is decreasing, its max is at $x=4$. Therefore, we choose $$K_2=\frac{1}{4\cdot 4^{3/2}}=\frac{1}{4\cdot 8}=\frac{1}{32}.$$ Then, we have by the theorem: $$E_1\le \frac{1}{32}\frac{|x-4|^2}{2!}.$$ Specifically, for $x=4.01$, the accuracy estimate is $$E_1\le \frac{1}{32\cdot 2}.01^2=\frac{.0001}{64}.$$ Definitely better then necessary!
Thus the answer, with this degree of accuracy, is $$\sqrt{4.01}=2.0225\pm .001.$$ $\square$
Definite integral
- (a) State the Fundamental Theorem of Calculus. (b) Use part (a) to evaluate
$$\int_{-1}^1 \sin \frac{x}{3} \, dx.$$
- (a) State the Fundamental Theorem of Calculus. (b) Use part (a) to evaluate
$$\frac{d}{dx}\int_0^{x}e^{t^2}\, dt.$$
- (a) Make a sketch of the left-end Riemann sums for $\int_0^1\sqrt{x}\, dx$ with $n=4$ intervals. (b) State the algebraic properties of the Riemann integral.
- Given $f(x)=x^{2}+1,$ write (but do not evaluate) the Riemann sum for the integral of $f$ from $-1$ to $2$ with $n=6$ and left ends as sample points. Make a sketch.
- Provide the definition of the definite integral via its Riemann sums. Make a sketch.
- The Fundamental Theorem of Calculus includes the formula $\int _a^bf(x)\, dx=F(b)-F(a)$. (a) State the whole theorem. (b) Provide definitions of the items appearing in the formula.
- (a) State the definition of the definite integral $\int _a^bf(x)\, dx$ and illustrate the construction with a sketch. (b) Use the definition to justify that $$\int _a^b cf(x)\, dx=c\int _a^b f(x)\, dx$$ for a constant $c$.
- Suppose $$\int_0^1f\, dx=2,\ \int_0^4f\, dx=0,\ \int_1^2f\, dx=2.$$ Find
$$\int_1^3f\, dx,\ \int_0^1(f(x)+3)\, dx,\ \int_2^4f\, dx.$$
- Suppose a function is defined by: $$F(x)=\int_2^xf\, dx.$$ Find, in terms of $F$, the following:
$$\int_0^4f\,dx,\ \int_1^2f\,dx,\ \int_0^{-1}f\,dx,\ \int_1^2(f(x)-1)\,dx.$$
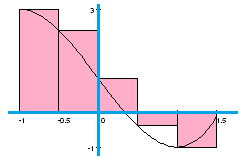
- Evaluate the Riemann sum of $f$ below on the interval $[-1,1.5]$ with $n=5$. What are its sample points? What does it estimate?
- Write (don't evaluate) the left-end Riemann sum of the integral $\int _0^5 f(x)\, dx$ for function $f$ shown below with $n=5$ intervals.
- Write the formula and illustrate with a sketch the left-end Riemann sum $L_4$ of the integral $\int _1^3 f(x)\, dx$ for the function plotted above.
- Write the mid-point Riemann sum that approximates the integral $\int _0^1 \sin x\, dx$ within $.01$.
- Set up the Riemann sum for the area of the circle of radius $R$ as the area between two curves, provide an illustration and the integral formula. Evaluate for extra 5 points.
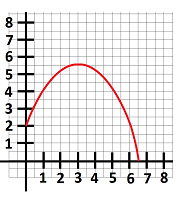
- Let $I=\int_ 2^8f\, dx$. (a) Use the graph of $y=f(x)$ below to estimate $L_{4},\ M_{4},\ R_{4}$. (b) Compare them to $I$.
- Complete the following statements:
- $(f(x)\cdot x^2)'=f'(x)\cdot x^2+...$;
- $\int x^{-1}\, dx=... $;
- $\int f'(x)\, dx=...$;
- $\int u\, dv=uv... $;
- $u=\cos t \ \Longrightarrow\ du=...$.
- Suppose that $F$ is an antiderivative of a differentiable function $f$. If $F$ is increasing on $[a,b]$, what can you say about $f$?
Integration
- Execute the following substitution in the integral (don't evaluate the resulting integral):
$$\int \sqrt{\cos x+\sin x}\, dx,\quad u=\sin x.$$
- Suppose $s(t)$ represents the position of a particle at time $t$ and $v(t)$ its velocity. If $v(t)=\sin t-\cos t$ and the initial position is $s(0)=0,$ find the position $s(1).$
- Evaluate
$$\int e^{3x}\, dx.$$
- Evaluate
$$\int_1^2(e^{x}+\sqrt {x}+x^{-1})\, dx.$$
- Evaluate
$$\int e^{x^2}2x\, dx.$$
- Evaluate
$$\int 2x\sin 5x\, dx.$$
- Evaluate $$\int_1^3 e^{t+1}\, dx.$$ Hint: watch the variables.
- Calculate:
$$\int \left(e^{\sin x^2+77}\right)' \, dx.$$
- Evaluate the integral by substitution
$$\int xe^{x^{2}}\, dx.$$
- Find all antiderivatives of the following function: $f(x)=e^{-x}$.
- Find the antiderivative $F$ of the function $f(x)=3x^{2}-1$ satisfying the initial condition $F(1)=0$.
- Evaluate the integral
$$\int_0^1x^3\, dx.$$
- Evaluate:
$$\int x^2\, dx - \int x^2\, dx.$$
- Evaluate:
$$\int x^{-2}\, dx - \int x^{-2}\, dx.$$
- Integrate by parts:
$$\int 3x e^{-x}\, dx.$$
- Use the table of integrals to evaluate:
$$\int \sin^{-1}{2x}\, dx.$$
- Evaluate:
$$\int_0^{1} \frac{1}{2x}\, dx.$$
- Use substitution to evaluate the integral:
$$\int _0^{\pi} \sin x \ \cos^2 x \, dx.$$
- Integrate by parts:
$$\int x(\ln x)^2\, dx.$$
- Use substitution to evaluate the integral:
$$\int _0^1 \frac{1}{\sqrt{4-x^2}}\, dx.$$
- Use the table of integrals to evaluate:
$$\int x^2(\sqrt{x^2-4}-\sqrt{x^2+9})\, dx.$$
- Evaluate
$$\int x \sin x\, dx.$$
- Use substitution $u=1+x^2$ to evaluate the integral
$$\int \sqrt{1+x^2} x^5\, dx.$$
- Use substitution to evaluate the integral:
$$\int _0^{\pi} \sin x \ \cos^2 x \, dx.$$
- Evaluate the improper integral:
$$\int_1^{\infty} \frac{1}{2x}\, dx.$$
- Find the antiderivative $F$ of the function $f(x)=e^{x}+x$ satisfying the initial condition $F(0)=1$.
Applications of integrals
- The region bounded by the graphs of $y=\sqrt{x},\ y=0,$ and $x=1$ is revolved about the $x$-axis. Find the surface area of the solid generated.
- A chord of a circle is a straight line segment whose end-points lie on the circle. Find the average length of a chord perpendicular to the diameter. What about parallel?
- Find the average length of a segment in a square parallel to (a) the base, (b) the diagonal.
- Find (by integration) the length of a circle of radius $r$.
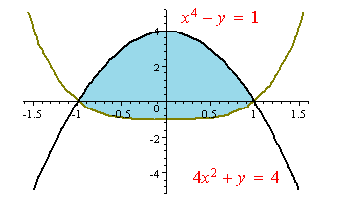
- Find the area enclosed by the curves below:
- Find the area of the region bounded by $y=x^2-1$ and $y=3$.
- Suppose $f$ is an integrable function. (a) Show that $f$ is also odd then $\int_{-a}^af\, dx=0$. (b) Suggest a related formula for an even $f$.
- Find the centroid of the region bounded by the curves $y=x^2,\ y=1$.
- Find the $x$-coordinate of the center of mass of the region between $y=x^2$ and $y=x^3$.
- Find the volume of a right circular cone of radius $R$ and height $h$ by any method you like.
- Compute the average area of the cross section of the sphere of radius $1$.
- Find the center of mass of the region below $y=2x$ for $0 \leq x \leq 1$.
- The volume of a solid is the integral of the areas of its cross-sections. Explain and justify using Riemann sums.
- The region bounded by the graphs of $y=x^{2}+1,\ y=0,\ x=0$ and $x=1$ is revolved about the $x$-axis. Find the volume area of the solid generated.
- The region bounded by the graphs of $y=x^{2}+1,\ y=0,\ x=0,$ and $x=1$ is revolved about the $y$-axis. Find the volume area of the solid generated.
- An aquarium $2$ m long, $1$ m wide, and $1$ m deep is full of water. Find the work needed to pump half of the water out of the aquarium (the density of water is $1000$ kg/m$^{3}$).
- Find the area of the surface of revolution around the $x$-axis obtained from $y=\sqrt{x},\ 4\le x\le 9$.
- Find the centroid of the region bounded by the curves $y=4-x^{2},\ y=x+2$.
- Find the area of the region bounded by $y=x^{2}-1$ and $y=3$.
- Find the area under the graph of the function $f(x)=e^x$ from $x=-1$ to $x=1$.
- Find the average value of the function $f(x)=2x^2-3$ on the interval $[1,3]$.
- Find the area of the region bounded by $y=\sqrt{x}$, the $x$-axis, and the lines $x=1$ and $x=4$.
Parametric curves
- Describe the motion of a particle with position $(x,y)$, where $$x=2+t\cos t,\ y=1+t\sin t,$$ as $t$ varies within $[0,\infty )$.
- Suppose the parametric curve is given by \[x=\cos3t,\ y=2\sin t.\] Set up, but do not evaluate, the integrals that represent (a) the arc-length of the curve, (b) the area of the surface obtained by rotating the curve about the $x$-axis.
- Suppose curve $C$ is the graph of function $y=f(x)$. (a) Find a parametric representation of $C$. (b) Find a parametric representation of $C$ that goes from right to left.
- Find all points on the curve \[x=\cos3t,\ y=2\sin t\] where the tangent is either horizontal or vertical.
- Sketch the following parametric curve: $$x=|\cos t|,\ y=|\sin t|,\ -\infty <t <+\infty.$$ Describe the curve and the motion.
- Sketch the following parametric curves:
- $x(t)=\frac{1}{t},\ y(t)=\sin t,\ t>0$;
- $x = \cos t,\ y= 2$;
- $x=1/t,\ y=1/t^{2},\ t>0$.
- (1) Sketch the parametric curve $x=\cos t,\ y=\sin 2t$. (2) The curve intersects itself. Find the angle of this intersection.
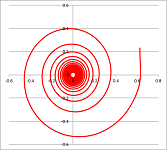
- Find an equation of the spiral converging to the origin as below:
- Plot this entire parametric curve: $x=\sin t,\ y=\cos 2t$.
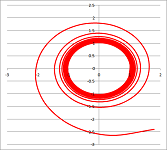
- Find a parametric representation of a curve similar to the one below, a spiral wrapping around a circle. What about one that is wrapping from the inside? (no proof necessary):
- Given a parametric curve $x=\sin t,\ y=t^2$. Find the line(s) tangent to the curve at the origin.
- Find a parametric representation of a curve that looks like the figure eight or a flower (no proof necessary).
Several variables
- Draw a few level curves of the function $f(x,y)=x^{2}+y$.
- The graph of function $y=g(x)$ of one variable is shown below. Suppose now that $z=f(x,y)=g(x)$ is a function of two variables, which depends only on $x$, given by the same formula. Find all points where the gradient of $f$ is equal to $0$.
- Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.
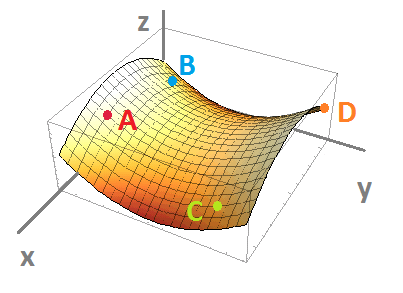
- Sketch the contour (level) curves of the function shown below, along with points $A,B,C,D$, on the $xy$-plane:
- Sketch the level curves of the function $f(x,y)=2xy+1$ for the following values of $z=-1,0,1,2.$
- Show that the limit doesn't exist:
$$\lim_{(x,y)\to (0,0)}\frac{xy}{x^{2}+y^{2}}.$$
- Draw the contour map (level curves) of the function $f(x,y)=e^{y/x}$. Explain what the level curves are.
- Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs:
$$f_x>0,\ f_{xx}>0,\ f_y<0,\ f_{yy}<0.$$
- The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Sketch the gradient for each on a separate $xy$-plane:
- Find the gradient of the function $f(x,y)=x^2y^{-3}$ at the point $(1,1)$. Use this information to sketch the graph of $f$ in the vicinity of this point. Explain.
- The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Provide the signs (positive or negative) of the partial derivatives of $f$ at these points. For example, $\frac{\partial f}{\partial x}<0$ at point $A$.
- Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.
- Make a sketch of contour (level) curves for the following function:
- The wave heights $h$ in the open sea depend on the speed $v$ of the wind and the length of time $t$ that the wind has been blowing at that speed. Values of the function $h=f(v,t)$ are recorded in the table below. Estimate the rate of change of $h$ with respect to $v$ when $v=40$ and $t=15$. Show your computations.
$$\begin{array}{c|ccc} v\backslash t &15 &20 &25\\ \hline 30 &16 &17 &18\\ 40 &25 &28 &31\\ 50 &36 &40 &45 \end{array}$$
- The contour (level) curves for a function are given below. They are equally spaced. Sketch a possible graph that produced it and describe it.
- Draw the contour map (level curves) of the following function of two variables:
- $g(x,y)=\ln(x+y)$;
- $f(u,v)=uv$;
- $h(x,y)=2x-3y+7$;
- $z=x^2+y^2$.
- Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs:
$$\begin{array}{c|ccccccccc} & 1&2&3&4\\ \hline f_x &+&+&-&+\\ f_{xx}&-&+&+&-\\ f_y &-&-&+&+\\ f_{yy}&-&+&-&+ \end{array}$$
- The graph of a function of two variables $z=f(x,y)$ is given below along with a point on the graph: 1. A, 2. B, 3. C, 4. D. Determine the signs of the derivatives $f_x,f_{xx},f_y,f_{yy}$ at that point:
Series
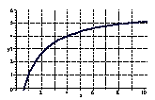
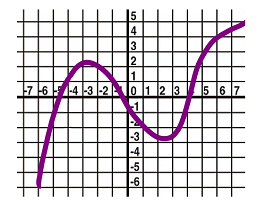
- Estimate the coefficients of the Taylor polynomial $T_1$ of order $1$ centered at $a=1$ of the function $f$ shown above. Provide a formula for this $T_1$. What about $T_2$; what is the sign of the coefficient of the next term that appears in $T_2$?
- What degree Taylor polynomial one would need to approximate $e^{.01}$ within $.001$? (Answers may vary and yours doesn't have to be perfect but it has to be justified.)
- (a) State the definition of absolute convergence. (b) Give an example of a series that converges but not absolutely.
- What degree Taylor polynomial one would need to approximate $\sin (-.01)$ within $.001$? Explain the formula: $$E_n \le K_{n+1} \frac{|x-a|^{n+1}}{(n+1)!}$$ and why you can choose $K_{n+1}=1$.
- Find the interval of convergence of the series:
$$\sum \frac{(x-2)^n}{n}.$$
- Explain how functions are represented by power series and how they both are differentiated. Demonstrate on $f(x)=e^x$.
- Find the Taylor polynomial of degree $4$ that would help to approximate $e^{1.01}$.
- (a) State the definition of the sum of a series. (b) Use (a) to prove the Sum Rule.
- Find the sum of the series
$$\sum _{n=0}^{\infty} \frac{(-1)^n+2}{3^n}.$$
- Test the following series for convergence (including absolute/conditional):
$$\sum \frac{(-1)^{n-1}}{(1.1)^n}.$$
- Find the radius and the interval of convergence of the series
$$\sum \frac{2(x+1)^n}{n^2}.$$
- Find the Taylor series centered at $a=1$ of the function $f(x)=x^4$.
- Apply the Integral Test to show that the $p$-series with $p=1/3$ diverges.
- Test the following series for convergence (including absolute/conditional):
$$\sum (-1)^{2n}\frac{1}{n^n}.$$
- Test the following series for convergence (including absolute/conditional):
$$\sum \frac{n^{1/2}}{n^2-1}.$$
- Find the radius and the interval of convergence of the series:
$$\sum \frac{(x-1)^n}{\sqrt{n}2^n}.$$
- Find the Taylor polynomial $T_{2}(x)$ of order $2$ centered at $a=\pi $ of the function $f(x)=\sin ^{2}x.$