Calculus II -- Spring 2018 -- final exam

MATH 230 -- Spring 2018 -- final exam

Name:_________________________ $\qquad$ 10 problems, 10 points each

• Write the problems in the given order, each problem on a separate page.
• Show enough work to justify your answers.

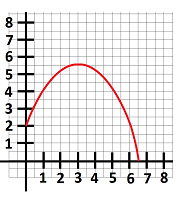
$\bullet$ 1. Write the formula and illustrate with a sketch the right-end Riemann sum $R_4$ of the integral $\int _1^3 f(x)\, dx$ for the function plotted below.

$\bullet$ 2. Suppose curve $C$ is the graph of a function $y=f(x)$. (a) Find a parametric representation of $C$. (b) Find a parametric representation of $C$ that goes from right to left.

$\bullet$ 3. The volume of a solid is the integral of the areas of its cross-sections. Explain and justify using Riemann sums.

$\bullet$ 4. Use substitution to evaluate the integral: $$\int_0^{\pi} \sin x \cos x dx.$$

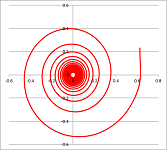
$\bullet$ 5. Find a parametric representation of the spiral converging to the origin as below:

$\bullet$ 6. Find the cubic Taylor polynomial one would need to approximate $\cos (.01)$.

$\bullet$ 7. (a) Plot this entire parametric curve: $x=\sin t,\ y=\sin^2 t$. (b) Find the line(s) tangent to the curve at the origin.

$\bullet$ 8. (a) State the definition of the sum of a series. (b) Find the sum of the series $$\sum _{n=0}^{\infty} \frac{(-1)^n+2}{3^n}.$$

$\bullet$ 9. (a) What is the interval of convergence of a power series? (b) Find the interval of convergence of the series: $$\sum \frac{(x+1)^n}{n^2}.$$

$\bullet$ 10. Explain how functions are represented by power series and how they both are differentiated and integrated. Demonstrate on the series: $$\sum \frac{(x+1)^n}{n^2}.$$