Calculus II -- Fall 2014 -- midterm

Name:_________________________ $\qquad$ 8 problems, 10 points each

• Justify every step you make with as thorough an explanation as possible, in English.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the new page.

$\bullet$ 1. Integrate by parts: $\int 3x e^{-x} dx.$

$\bullet$ 2. Evaluate the improper integral: $\int_1^{\infty} \frac{1}{2x} dx.$

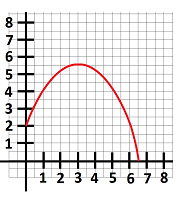
$\bullet$ 3. Write (don't evaluate) the left-end Riemann sum of the integral $\int _0^5 f(x) dx$ for function $f$ shown below with $n=5$ intervals.

$\bullet$ 4. Estimate the coefficients of the Taylor polynomial $T_1$ of order $1$ centered at $a=1$ of the function $f$ shown above. Provide a formula for this $T_1$. What about $T_2$; what is the sign of the coefficient of the next term that appears in $T_2$?

$\bullet$ 5. Use the table of integrals to evaluate: $\int \sin^{-1}{2x}\ dx.$

$\bullet$ 6. Find the centroid of the region bounded by the curves $y=x^2,y=1$.

$\bullet$ 7. What degree Taylor polynomial one would need to approximate $e^{.01}$ within $.001$? (Answers may vary and yours doesn't have to be perfect but it has to be justified.)

$\bullet$ 8. Use substitution to evaluate the integral: $\int _0^{\pi} \sin x \ \cos^2 x \ dx.$

$$\begin{array}{lll} \\ \\ \\ \\ \\ \\ \\ \hline \end{array}$$