Calculus II -- Fall 2014 -- final exam

Name:_________________________ $\qquad$ 12 problems, 10 points each

• Justify every step you make with as thorough an explanation as possible, in English.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the page.

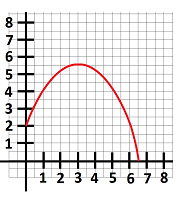
$\bullet$ 1. The graph $y=f(x)$ of function $f$ is sketched below (it's not a parabola). Based on the graph, estimate the value of the derivative $f'$ of $f$ for $x=0$ and $x=5$. What can you say about $f' '$?

$\bullet$ 2. Write the formula and illustrate with a sketch the left-end Riemann sum $L_4$ of the integral $\int _1^3 f(x)\ dx$ for the function plotted above.

$\bullet$ 3. Find the $x$-coordinate of the center of mass of the region between $y=x^2$ and $y=x^3$.

$\bullet$ 4. Evaluate: $\int_0^{1} \frac{1}{2x} dx.$

$\bullet$ 5. Use substitution to evaluate the integral: $\int _0^{\pi} \sin x \ \cos^2 x \ dx.$

$\bullet$ 6. (a) State the definition of absolute convergence. (b) Give an example of a series that converges but not absolutely.

$\bullet$ 7. What degree Taylor polynomial one would need to approximate $\sin (-.01)$ within $.001$? Explain the formula: $E_n \le K_{n+1} \frac{|x-a|^{n+1}}{(n+1)!}$ and why you can choose $K_{n+1}=1$.

$\bullet$ 8. (a) Plot these points in polar coordinates: $(r,\theta )=$ $(0,1)$, $(1,0)$, $(1,\pi)$, $(2,3\pi)$. (b) Sketch these three polar curves: $r=1,\ \theta=0,\ r=\theta$.

$\bullet$ 9. Evaluate the limit: $\lim_{n\to \infty}\ln \left({\frac{n}{n+1}} \right)$.

$\bullet$ 10. Plot this entire parametric curve: $x=\sin t,y=\cos 2t$.

$\bullet$ 11. Find the interval of convergence of the series: $\sum \frac{(x-2)^n}{n}.$

$\bullet$ 12. Explain how functions are represented by power series and how they both are differentiated. Demonstrate on $f(x)=e^x$.