Calculus III -- Spring 2014 -- midterm

Name:_________________________

10 problems, 10 points each

• Justify every step you make with as thorough explanation as possible.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the page.

$\bullet$ 1. Sketch the following parametric curve:

1. $x(t)=\frac{1}{t}, y(t)=\sin t,t>0$;
2. $< x, y > = < \cos t, 2 >$;
3. $r=2^t{\bf i}+2^{2t}{\bf j}$;
4. $x=1/t,y=1/t^{2},t>0$.

$\bullet$ 2. Find all points on the curve $x=3\cos t,y=2\sin t$ where the tangent vector points in the following direction: 1. up, 2. left, 3. down, 4. right.

$\bullet$ 3. Sketch a curve on the plane the curvature of which is: 1. increasing, 2. decreasing, 3. constant non-zero, 4. zero.

$\bullet$ 4. Suppose a ball in thrown horizontally at speed $v$ feet per second by a person $h$ feet tall. Represent the motion as a parametric curve in the $3$-dimensional space.

$\bullet$ 5. Draw the contour map (level curves) of the following function of two variables:

1. $g(x,y)=\ln(x+y)$;
2. $f(u,v)=uv$;
3. $h(x,y)=2x-3y+7$;
4. $z=x^2+y^2$.

$\bullet$ 6. Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs: $$\begin{array}{cccccccccc} & 1&2&3&4\\ f_x &+&+&-&+\\ f_{xx}&-&+&+&-\\ f_y &-&-&+&+\\ f_{yy}&-&+&-&+ \end{array}$$

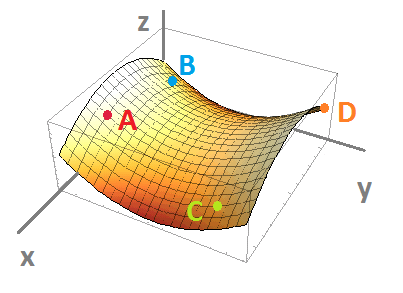
$\bullet$ 7. The graph of a function of two variables $z=f(x,y)$ is given below along with a point on the graph: 1. A, 2. B, 3. C, 4. D. Determine the signs of the derivatives $f_x,f_{xx},f_y,f_{yy}$ at that point:

$\bullet$ 8. Find the partial derivatives of the following function of three variables:

1. $g(x,y,z)=z\sqrt{x+y}$;
2. $u=1$;
3. $w=e^{x+y+z}$;
4. $f(u,v,w)=uv+e^w$.

$\bullet$ 9. Find the best linear approximation of the function $f(x,y)=xe^{y}$ at the following point: 1. $(0,0)$, 2. $(0,1)$, 3. $(1,1)$, 4. $(1,0)$.

$\bullet$ 10. From the definition, find the directional derivative of the function $f(x,y)=2x-3y$ at the point $(1,1)$ in the direction of the following vector: 1. $<3,0>$, 2. $-2{\bf j}$, 3. $<1,1>$, 4. $<-1,-1>$.