Algorithm for binary images

Case (a) - the new edge connects two different 0-cycles.

Case (b) - the new edge connects a 0-cycle to itself.

Case (c) - the new edge connects a 1-cycle to itself.

Case (d) - the new edge connects a 1-cycle to a 0-cycle (inside).

Topological analysis of a binary image. We construct its topology graph.

The time complexity of the algorithm is O(n²), where n is the number of pixels in the image.

Outline:

1. All pixels in the image are ordered in such a way that all black pixels come before white ones.
2. Following this order, each pixel is processed:
   1. add its vertices, unless those are already present as parts of other pixels;
   2. add its edges, unless those are already present as parts of other pixels;
   3. add the face of the pixel.
3. At every step, the graph is given a new node and arrows that connect the nodes in order to represent the merging and the splitting of the cycles:
   1. adding a new vertex creates a new component;
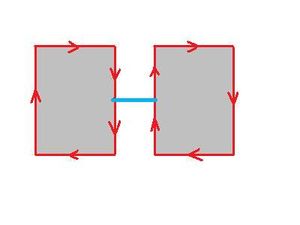
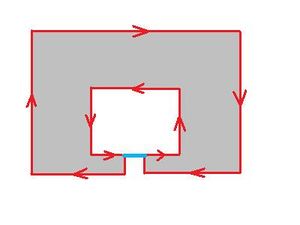
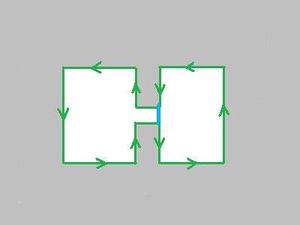
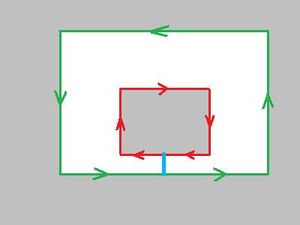
   2. adding a new edge may connect two components, or create, or split a hole;
   3. adding the face to the hole eliminates the hole.

Only step 3.2 is of any complexity. However, thanks to cell decomposition of images, there are only 4 cases to consider. See Pseudocode for binary images

The algorithm is incremental. As pixels are added one by one, the topology of the image changes.

Adding a whole pixel, there are many possible cases to consider. Here's just one:

Now imagine that instead of an edge we are adding a whole pixel at once. It is adjacent to $8$ other pixels. These are the consequences:

• There are $2^8$ possible arrangements - only $1$ arrangement if you are adding an edge.
• These pixels may belong to up to $4$ different objects - only $2$ objects if you are adding an edge.
• The number of cases to consider is even hard to count - only $4$ cases if you are adding an edge.

Just imagine what happens in $3D$! Finally let's consider the way we keep record of cells in images. Once again we stick with a familiar approach - via analytic geometry. Vertices are points so they can be recorded as pairs of integers. Edges are vectors, so an edge is recorded by its initial point and the direction - $4$ integers. What about pixels? A pixel is recorded by the coordinate of its upper left corner - $2$ integers. Observe that if the image is $X \times Y$, the coordinates of pixels run from $0$ to $X-1 (Y-1)$, while the coordinates of vertices run from $0$ to $X (Y)$. What about 3D? (Exercise.)