This site is being phased out.
Advanced Topology: midterm
From Mathematics Is A Science
Jump to navigationJump to searchMATH 632 Advanced Topology Spring 2013 ......................... NAME_____________
MIDTERM: 10 problems, 10 points each
Instructions:
- Justify all your steps and conclusions.
- For justification you can use all theorems stated in class, unless that's what you are asked to prove. While making references be as specific as possible.
- You cannot use for justification: the results that appeared in homework, quizzes, or other classes.
Problems
- Show that the set of differential forms is a vector space.
- Compute (a) $x^2dx^1$ on $<1,2,3>$ at $(3,2,1)$; (b) $dx^1 \wedge dx^3 + x^1dx^2 \wedge dx^4$ on the pair $<-1,0,1,1>, <0,-1,0,1>$ at $ (1,0,0,0)$.
- Simplify: $$2dx^1 \wedge dx^3 \wedge dx^2 + 3dx^2 \wedge dx^1 \wedge dx^2 - dx^2 \wedge dx^3 \wedge dx^1 .$$
- Compute the exterior derivative of $xydx \wedge dy + yz dy \wedge dz + dz \wedge dx$.
- Suppose $\alpha, \beta, \gamma \in \Omega ^1({\bf R}^3)$ are linearly independent. Assuming $dd(\alpha)=dd(\beta)=dd(\gamma)=0$, prove that $dd(\psi ^1)=0$.
- Given that the 2nd de Rham cohomology of $3$-space with a point removed is $1$-dimensional: $\Omega^2_{dR}({\bf R}^3-\{0\})={\bf R}$, list its cohomology classes. No proof required.
- Prove that the boundary of a boundary is zero, in dimension $2$ (for cubical complexes).
- For discrete forms in ${\bf R}^3$ compute: (a) $dx \wedge dy$; (b) $dx \wedge \psi ^2$, where the latter is equal to $1$ on a single square, say $\alpha$, parallel to the $xy$-plane and equal to $0$ elsewhere.
- Compute the exterior derivative of the following form:
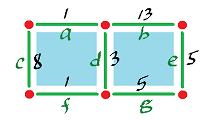
- (a) Describe the vector spaces of discrete differential forms for the complex: (b) Evaluate the cohomology of the complex above (just the answer).