This site is being phased out.
A new look at continuity
Contents
From accuracy to continuity
The idea of continuity can be introduced and justified by considering the accuracy of a measurement.
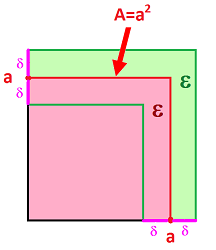
Suppose we have a collection of square tiles of various sizes and we need to find the area $A$ of each of them in order to know how many we need to cover the whole floor.
The answer is, of course, to measure the side, $x$, of each tile and then compute $$A=x^2.$$ For example, we have: $$x=10\Rightarrow A=100$$ (in inches).
But what if the measurement isn't fully accurate? What if there is always some error? It's never $x=10$ but, say, $$x=10 \pm .3.$$ As a result, the computed value of the area of the tile -- what we care about -- will also have some error! Indeed, the area won't be just $A=100$ but $$A=(10 \pm .3)^2 .$$ Therefore, $$\begin{array}{lll} A&=10^2 \pm 2 \cdot 10 \cdot .3 +.3^2 \\ &=100.09 \pm 6. \end{array}$$ The meaning of the result is that the actual area must be somewhere within the interval $(94.09,106.09)$.
Suppose next that we can always improve the accuracy of the measurement of the side of the tile $x$ -- as much as we like. The question is, can we also improve the accuracy of the computed value of $A$ -- to our, or somebody else's, satisfaction? The standard of accuracy might change...
What do we mean by that? Suppose $x=10$. The above computation shows that if the desired accuracy of $A$ is $\pm 5$, we haven't achieved it with the given accuracy of measurement $x$, which is of $\pm .3$. We can easily show, however, that $\pm .2$ would solve the problem: $$\begin{array}{lll} A&=(10 \pm .2)^2=10^2 \pm 2 \cdot 10 \cdot .2 +.2^2 \\ &=100.04 \pm 4. \end{array}$$ It follows that the actual area must be within $4.04$ from $100$.
Let's rephrase this problem in order to solve it for all possible values of the desired accuracy of $A$.
Let's assume that the measurement of the side is $a$ and, therefore, the assumed area $A$ is $a^2$. Now suppose we want the accuracy of $A$ to be some small value $\varepsilon >0$ or better. What accuracy $\delta$ of $x$ do we need to be able to guarantee that?
Suppose the actual length is $x$ and, therefore, the actual area is $A=x^2$. Then we want to ensure that $A$ is within $\varepsilon$ from $a^2$ by making sure that $x$ is within $\delta$ from $a$. What should $\delta$ be?
To rephrase algebraically, we want to find $\delta$ such that $$|x-a| <\delta \Rightarrow |x^2-a^2|<\varepsilon.$$
The definition suggested by the above discussion is familiar from calculus.
Definition. A real-valued function $f$ is called continuous at $x=a$ if for any $\epsilon >0$ there is $\delta >0$ such that $$|x-a| <\delta \Rightarrow |f(x)-f(a)|<\varepsilon.$$
Thus the answer to our question is:
- yes, we can always improve the accuracy of the computed value of $A=x^2$ -- to anybody's satisfaction -- by improving the accuracy of the measurement of $x$.
The reason to be quoted is that $f(x)=x^2$ is continuous at $x=10$.
Note: The word “continuous” itself is justified on other grounds.
Exercise. Prove that $f(x)=x^2$ is continuous at $x=0,x=1,x=a$.
Exercise. Carry out this kind of analysis for: a thermometer put in a cup of coffee to find its temperature. Assume that the thermometer gives perfect readings. Hint: it'll take time for it to warm up.
To further illustrate this idea, consider a different situation. Suppose we don't care about the area anymore; we just want to fit these tiles into a strip $10$ inches wide. We take a tile and if it fits, it is used; otherwise it is discarded.
So, we still get a measurement $a$ of the side of the tile but our real interest is whether $a$ is less or more than $10$.
Just as in the previous example, we don't know the actual length $x$ exactly; it's always within some limits: $5.0 \pm 0.5$ or $a \pm \delta$. Here $\delta$ is the accuracy of measurement of $x$. The algebra is much simpler than before. For example, if the length is measured as $11$, we need the accuracy $\delta=1$ or better to make the determination. It's the same for the length $9$.
But what if the measurement is exactly $10$? Even if we can improve the accuracy, i.e., $\delta$, as long as $\delta > 0$, we can't know whether $x$ is larger or smaller than $10$.
Let's define a function $f$: $$f(x)=\begin{cases} 1 \quad\text{ (pass) } & \text{ if } x \le 10, \\ 0 \quad\text{ (no pass) } & \text{ if } x > 10. \end{cases}$$
Suppose we need the accuracy of $y = f(x)$ to be $\varepsilon = 0.5$. Can we achieve this by decreasing $\delta$? In other words, can we find $\delta$ such that $$|x-10|<\delta \Rightarrow |f(x)-1|<\varepsilon ?$$ Of course not: $$x>10 \Rightarrow |f(x)-1|=|0-1|=1.$$
Thus the answer to our question is:
- No, we cannot always improve the accuracy of the computed value of $f(x)$ -- to anybody's satisfaction -- by improving the accuracy of the measurement of $x$.
The reason to be quoted is that $f$ is discontinuous at $x=10$.
Exercise. Carry out this kind of analysis for: the total test score vs. the corresponding letter grade. What if we introduce A-, B+, etc.?
Thus, the idea of continuity of the dependence of $y$ on $x$ is:
- We can ensure the desired accuracy of $y$ by increasing the accuracy of $x$.
Exercise. In addition to being continuous, $f(x)=x^2$ is also differentiable. How does that help with the accuracy issue? Hint: there is a simple dependence between $\varepsilon$ and $\delta$.
Continuity in a new light
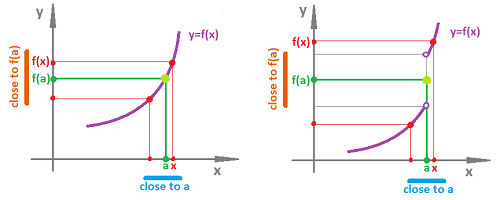
The discussion in the last subsection reveals that continuity of function $f : {\bf R} \to {\bf R}$ at point $x=a$ can be introduced in terms of closeness (proximity) of its values, informally:
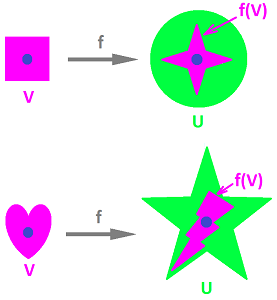
This description applies to the function shown on the left:
On the right, even though $x$ is close to $a$, $f(x)$ does not have to be close to $f(a)$: the discontinuity of the function does not allow us to finely control its output by controlling the input.
Let's rephrase the second part of the continuity definition:
- for any $\varepsilon > 0$ there is a $\delta > 0$ such that
- $|x - a| < \delta \Rightarrow |f(x) - f(a)| < \varepsilon$.
It is advantageous to restate this part as:
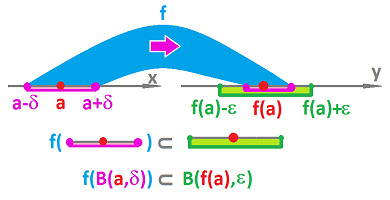
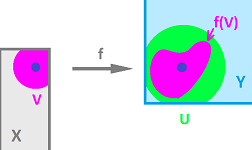
Next, we use a concept that will help to keep things more compact. It is the concept of the image of subset $A \subset X$ under function $f:X \to Y$, defined as $$f(A) := \{f(x) : x \in A \}.$$
Now the last formulation of continuity means simply that $f$ takes a certain subset of the $x$-axis to a subset of the $y$-axis: $$f\left( (a-\delta,a+\delta) \right) \subset \left( f(a)-\varepsilon, f(a)+\varepsilon \right).$$ These sets are open intervals:
We look at these intervals as $1$-dimensional “balls”, while in general, we define an open ball in ${\bf R}^n$ as: $$B(p,d)=\{u : || u-p || < d \}.$$ We simply used the norm, $$||x||=||(x_1,,...,x_n)||:=\sqrt { \sum _{i=1}^n |x_i|^2 },$$ to replace the absolute value.
In mathematics, we see a lot of examples of functions between higher-dimensional Euclidean spaces $f:{\bf R}^n \to {\bf R}^m$: parametric curves, parametric surfaces, vector fields, etc. We can accommodate the need to understand continuity of these functions by using the same idea of proximity: $$||x - a|| < \delta \Rightarrow || f(x) - f(a) || < \varepsilon.$$
Then our definition becomes even more compact, as well as applicable to all dimensions:
Definition. A function $f:{\bf R}^n \to {\bf R}^m$ is continuous at point $x=a$ if
- for any $\varepsilon > 0$ there is a $\delta > 0$ such that
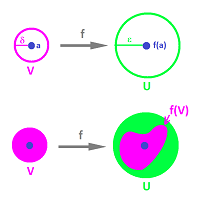
- $f\left( B(a,\delta) \right) \subset B \left( f(a), \varepsilon \right) .$
The final simplification of the second part is: $$f( V ) \subset U,$$ where $$V=B(a, \delta), \quad U=B \left( f(a) , \varepsilon \right).$$ In dimension $2$, the relation between these sets is illustrated as follows:
Exercise. Using the definition, prove that constant functions $c:{\bf R}^n \to {\bf R}^m$ and the identity function are continuous.
Exercise. Prove that the norm is continuous.
Exercise. Prove that the composition of continuous functions is continuous.
Exercise. Provide an analog of this definition for “continuity from the left and right” of a function the domain of which is a closed interval such as $[0,1]$. For a function of two variables, what if the domain is a closed square, a closed disk?
Continuity on subsets
Our interest is mainly algebraic topology. Consequently, apart from pointing out monstrosities to avoid, we will keep our attention limited to
- “nice” subsets of Euclidean spaces, such as cells, and
- those subsets “nicely” glued together.
We have already seen an example: realizations of graphs. When we come back to algebra, it will explain how these pieces fit together globally to form components, holes, voids, etc.. Right now, in a way, we are interested in local topological properties, such as continuity.
Now, an example of an especially “nice” set is $$\bar{B}(a,\delta)= \{u\in {\bf R}^n : ||u-a|| \le \delta \}, $$ the closed ball centered at $a\in {\bf R}^n$ of radius $\delta$. In dimension $1$, this is simply a closed interval, yet functions defined on such a set won't fit into the last definition of continuity.
For example, continuity from the left and right has to be treated as an exception, i.e., as a separate definition. Suppose we are considering continuity of a function $f$ at $x=a$ when its domain is $[a,b]$. Then a half of the interval $(a-\delta,a+\delta)$ lies outside the domain! Our answer is to verify the proximity condition only for the points inside $[a,b]$ and ignore the rest. This way it doesn't matter how the domain fits into some bigger space.
To accommodate this idea, we retrace the analysis in the last subsection, for a function $$f:X \to Y$$ with $$X \subset {\bf R}^n, Y \subset {\bf R}^m.$$ Recall that this notation simply means that $$x\in X \Rightarrow f(x)\in Y.$$
We will need to adjust the second part of the definition a tiny bit more:
- $||x - a|| < \delta,x \in X \Rightarrow || f(x) - f(a) || < \epsilon.$
With this little addition, $x \in X$, we have sidestepped the issue of continuity from the left/right and, in higher dimensions, the case when a point $x$ is close to $a$ but outside the domain of the function.
As before, the inequalities indicate simply that $f$ takes $x$ that lies in a certain subset of the domain of $f$ to $y=f(x)$ in another subset of its range:
- if $x \in B(a, \delta)$ and $x \in X$ then $f(x) \in B(f(a), \epsilon)$.
Of course, it was assumed from the beginning that $f(x)\in Y$. The condition can be further re-written as
- $f \left( B(a, \delta) \cap X \right) \subset B \left( f(a) , \epsilon \right) \cap Y.$
Adding “$\cap Y$” is not a matter of convenience; we just want to be clear that we don't care about anything outside $X$ and $Y$.
Let's state this most, for now, compact definition.
Definition. A function $f:X \to Y$ with $X \subset {\bf R}^n, Y \subset {\bf R}^m$ is called continuous at $x=a$ if
- for any $\epsilon >0$, there is $\delta$ such that
- $f( V ) \subset U,$
where $$V=B(a, \delta) \cap X, \quad U=B \left( f(a) , \epsilon \right) \cap Y.$$
In dimension $2$, the relation between these sets is illustrated as follows:
Exercise. Show how this new definition incorporates the old definition of one-sided continuity.
The following is familiar.
Definition. A function $f$ is called continuous if it is continuous at every point of its domain.
The question, “What do you know about continuity of $1/x$?” might be answered very differently by different students:
- a calculus 1 student: “$1/x$ is discontinuous... well, it's discontinuous at $x=0$ and continuous everywhere else.”
- a topology student: “The function $f:(-\infty,0)\cup (0,\infty) \to {\bf R}$ given by $f(x)=1/x$ is continuous.”
...because we don't even consider continuity at a point where the function is undefined.
Exercise. Show that continuity of a function defined on the $x$-axis (its domain) as a function of $(x,y)$ is equivalent to its continuity as a function of $x$ only.
There is still an even more profound generalization to be made. We already test for continuity of $f$ from the inside of its domain $X$, without mention of any $x \not\in X$. Now would like to take this idea one step further and avoid referring to open balls that come from the ambient Euclidean spaces.
The intrinsic definition of continuity
Let's start with the case of $X={\bf R}^n,\ Y={\bf R}^m$. Suppose that
- $\gamma _X$ is the set of all open balls in $X={\bf R}^n$, and
- $\gamma _Y$ is the set of all open balls in $Y={\bf R}^m$.
We can restate the definition in a more abstract form:
Exercise. Prove that this definition is equivalent to the original.
Now, once again, what if the domain is a subset $X$ of the Euclidean space?
Then, we just choose for $\gamma _X$, instead of the open balls, the intersections of the open balls with the subset $X\subset {\bf R}^n$: $$\gamma _X := \{ B(x,\delta)\cap X:\ x\in X,\delta>0 \}.$$ The definition above remains the same.
This approach fits into our strategy of studying the intrinsic properties of objects as if anything outside $X$ simply doesn't exist!
Moreover, if our interest is to study $X$, we need to consider all and only functions with domain $X$. For the new definition, we will make no reference to the Euclidean space that contains $X$. For that, we just need to determine what collections $\gamma _X$ are appropriate.
First we observe that these balls can be easily replaced with sets of any other shape:
The importance of these intervals, disks, and balls for continuity is the reason why we start studying topology by studying these collections of sets. We will call them neighborhoods. For example, $B(a, \delta)$ is a ball neighborhood of $a$.
Second, we notice that continuity is a local property and, therefore, we don't need a single yardstick to measure closeness (i.e., distances between points) throughout $X$ (or $Y$). We just need the ability for each $a \in X$, to answer the question: “How close is $x$ to $a$?” And the new answer doesn't look that different:
- Calculus 1: “It's within $\delta$”;
- Topology: “It's within $V$”.
The news is, all references to numbers are gone!
In order to have a meaningful concept of continuity, we need these collections of neighborhoods to satisfy certain properties...
First of course, we want to be able to discuss continuity of $f:X\to Y$ at every point $a\in X$. So, these neighborhoods have to cover the whole set:
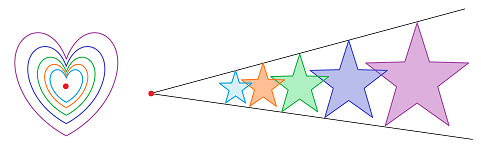
Second, we want to be able to zoom in on every point -- to detect breaks in the graphs of functions. So, we should be able to “refine” the collection:
This is how we understand the refining process illustrated with disks:
To summarize, we require:
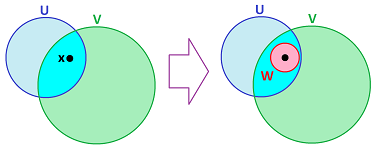
- (B1) $\cup \gamma = X$;
- (B2) for any two neighborhoods $U, V\in \gamma$ and any point $c\in U\cap V$ in their intersection, there is a neighborhood $W\in \gamma$ of $c$ such that $W \subset U \cap V$.
We will demonstrate that this is all the extra structure we need to have on an arbitrary set $X$ to be able to define and study continuity!
Definition. Suppose $X$ is any set. Any collection $\gamma$ satisfying properties (B1) and (B2) is called a basis of neighborhoods in $X$.
And the new definition of continuity is wonderfully compact:
Definition. Given two sets $X,Y$ with bases of neighborhoods $\gamma_X,\gamma_Y$, function $f:X\to Y$ is continuous if for any $U \in \gamma _Y$ there is $V \in \gamma _X$ such that $f( V ) \subset U$.
Exercise. Prove that the definition of continuity in the last subsection satisfies this definition.