Separation axioms

Redirect to:

• Manifolds#The separation axioms

Suppose X is a Euclidean space. Then

any two distinct points have neighborhoods that don't intersect.

Indeed, if $x,y$ are these points in $X$, we define: $$U = B(x,r) {\rm \hspace{3pt} and \hspace{3pt}} V = B(y,r), {\rm \hspace{3pt} where \hspace{3pt}} r = ||x-y||/2$$

($|| \cdot ||$ is the Euclidean norm). A topological space satisfying this condition is called Hausdorff. (Of course this is a topological invariant.)

This is indeed a "separation" axiom as we separate the two points from each other by means of disjoint open sets:

for any $x,y \in X, x \neq y$, there are open sets $U, V$ such that $x \in U, y \in V$ and $U \cap V = \emptyset$.

In the anti-discrete space, $U = V = X$, so it's not Hausdorff (unless it's a single point).

In the discrete space, one can always choose $U = \{x \}, V = \{y \}$, so it's Hausdorff.

The real line ${\bf R}$ equipped with the ray topology $\{(p, \infty ) \colon p \in {\bf R} \}$ isn't Hausdorff because any two rays intersect.

Theorem. If $X$ is Hausdorff, then $\{x \}$ is closed for any $x \in X$.

Proof. The idea is to separate $x$ from every other point in $X$. Indeed, if $y \neq x$, then, by definition,

there are open sets $U, V$ such that $x \in U, y \in V_y$ and $U \cap V_y = \emptyset$.

We don't care about $U$, but we care that $x$ does not belong to any $V_y$. Then $$X \setminus \{x \} = \bigcup \{V_y \colon y \in X \setminus \{x \} \}.$$ Hence this is an open set and, therefore, $\{x \}$ is closed. $\blacksquare$

Some things are simpler when the space is Hausdorff.

Theorem. Suppose $X$ is Hausdorff. If a subset $A$ of $X$ is compact, then it is closed.

Theorem. Suppose $X$ is compact and $Y$ is Hausdorff. If $f \colon X \rightarrow Y$ is continuous, one-to-one, and onto, then $f$ is a homeomorphism.

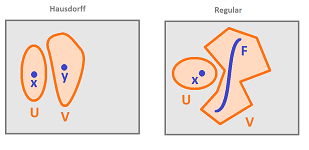
A higher degree of separation than Hausdorff is when a point and a closed set can be "separated" by neighborhoods:

for any closed set $F$ and a point $x$ that does not belong to $X$, there are open sets $U, V$ such that $x \in U, F \subset V$ and $U \cap V = \emptyset$.

If, in addition, every singleton $\{x \}$ in $X$ is closed, $X$ is called regular.

Clearly, a discrete space is regular and an anti-discrete is not.

The following is obvious.

Theorem. Every regular space is Hausdorff.

A partial converse is below.

Theorem. Every compact Hausdorff space is regular.

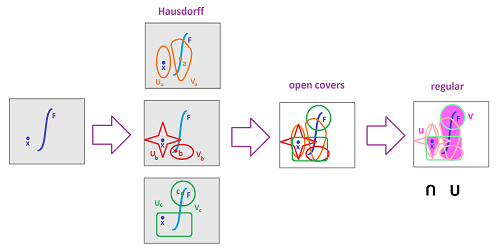
Proof. Suppose $F$ is a closed subset of $X$, $x \in X \setminus F$.

The idea is to "separate" $x$ from each $y$ in $F$ and then use these open sets to "separate" $x$ and the whole $F$. For the Hausdorff $X$ we have:

for any $y \in F$, there are open sets $U_y$, $V_y$ such that $x \in U_Y$, $y \in V_y$ and $U_y \cap V_y = \emptyset$.

Since $X$ is compact and $F$ is closed, $F$ is compact too. Hence the open cover $$\alpha = \{V_y \colon y \in F \}$$ has a finite subcover, $\alpha'$. Then $$\alpha' = \{V_y \colon y \in F' \},$$ where $F'$ is a finite subset of $F$. Now define $$U = \bigcap \{U_y \colon y \in F' \} {\rm \hspace{3pt} and \hspace{3pt}} V = \bigcup \{ U_y \colon y \in F' \}.$$ Both are open. $\blacksquare$