Quotients of vector spaces

Redirect to:

• Homology groups of graphs#Quotients in algebra

Introduction

Given a vector space $L$ and a subspace $M$. How do we "remove" $M$ from $L$?

Unfortunately, $L \setminus M$ isn't a vector space!

The next idea how one may to answer the question is to consider the orthogonal complement of $M$ (all vectors orthogonal to $M$) in $L$.

But what if the space might not have the inner product in the first place? Then the concept of orthogonality simply isn't available...

The idea is fruitful though and we can implement something similar with a related construction based on equivalence relation and quotients of sets.

Our approach is that instead of physically removing $M$ point-by-point, we "collapse" it to $0$:

$x \sim 0$ if $x \in M$,

to begin with.

The question now is of course, what about the rest of $L$?

For the end result to be a vector space we need to make sure that the equivalence relation we are constructing respect the algebraic operations of $L$. We then extend the above equivalence $\sim$ to the whole $L$ by invoking its algebra:

$x \sim y$ if $x - y \sim 0$,

or

$x \sim y$ if $x - y \in M$.

Then the equivalence class of $v \in L$ is $$[v] = \{x: x - v \in M \} = \{x = v + m, m \in M \} = v + M.$$ It follows:

Theorem 1. The equivalence class of $v \in L$ in $L/M$ is the affine subspace resulted from $M$ shifted by $v$: $$[v] = v + M.$$

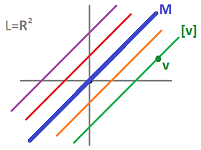
For example, suppose $M$ is the diagonal in $L={\bf R}^2$: $$M = \{(r,r): r \in {\bf R} \}.$$

Then each equivalence class is a line:

We can clearly see the partition induced by this equivalence relation.

Further we have: $$[v] = \{v + (r,r): r \in {\bf R} \} = v + M.$$ In other words, the elements of $L / M$ are the lines parallel to $M$ which appear in a 1-1 correspondence with the points on the other diagonal line.

Definitions and theorems

Theorem 2. The quotient set $L/M$ is a vector space with the operations:

• $[x] + [y] = [x + y],x,y\in L$, and
• $s[x] = [sx],x\in L,s\in {\bf R}$.

It is denoted by $L/M$ as we've chosen to "divide" rather than "subtract". Indeed: $${\bf R}^n / {\bf R}^m = {\bf R}^{n-m}, n>m.$$

Theorem 3. For a finitely-dimensional vector space $L$ and its subspace $M$, $$\dim L / M = \dim L - \dim M.$$

Note that the dimension behaves like the logarithm!

Then it's easy to see that the operations on $L/M$ are well defined: $$[v] + [u] = (v + M) + (u + M) = v + u + (M + M) = v + u + M = [v + u],$$ $$q[v] = q(v + M) = qv + qM = qv + M = [qv].$$

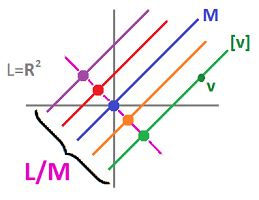
In the above example, we can collapse the equivalence classes in a particular way so that they "form" a line. The line is $y = -x$ and it's perpendicular to $M$. Then, informally, $$L \cong M \times L/M. $$ However, a choice of any other line, except $M$ itself, would be as an valid illustration of this idea.

In this sense, the projection $p: L \rightarrow L/M$ is given by $$p(x,y) = ( (y-x)/2, -(y-x)/2 ).$$

Theorem. For inner product spaces, the quotient space of $L$ over $M$ is a vector subspace isomorphic to the orthogonal complement of $M$: $$L/M\cong M^{\perp}.$$

This is where one can find the basis of $L/M$ (in the example: $[(1,-1)]$).

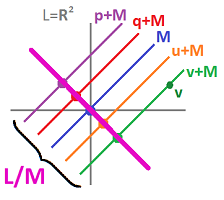
To illustrate $L/M={\bf R}^3 / {\bf R}^2$, these are the equivalence classes, algebraically:

and as sets:

Exercise. Illustrate ${\bf R}^3 / {\bf R}^1$.

Proof of Theorem 2. We need to show that the addition on $L/M$ given by $$[x]+[y]=[x+y]$$ is well defined, i.e., the definition is independent from a choice of $x,y$ as representatives of these equivalence classes. In other words, we need to show that $$[x]=[x'],[y]=[y']\Rightarrow [x+y]=[x'+y'],$$ or $$x\sim x',y\sim y'\Rightarrow x+y\sim x'+y'.$$ or $$x-x'\in M,y-y'\in M \Rightarrow (x+y) - (x'+y')\in M.$$ That follows directly from the fact that $M$, as a linear subspace, is closed under the operations of $L$. Same for scalar multiplication. $\blacksquare$

The quotient operator

The quotient function $$q: L \rightarrow L/ _{\sim} =L/M$$ is defined by $$q(x) = [x].$$ This is a linear operator and $\ker q=M$. Exercise.

Quotients of linear operators

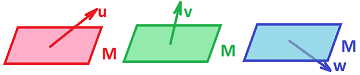
An equivalence relation on a vector space creates a new space. If this happens to two spaces, what happens to a linear map between them? Is there always a corresponding map between the quotients?

Yes, if it respects the equivalence relation.

Indeed, if $$f:L \rightarrow N$$ is a linear map between two vector spaces with subspaces $L'$ and $N'$, then, as usual, the quotient of $f$ is a function $$f:L/L' \rightarrow N/N'$$ (or $f_*$, etc) given by $$f([x])=[f(x)].$$ It is supposed to take equivalence classes to equivalence classes.

The usual question is "Is it well-defined?", plus "Is it linear?"

For the image of an equivalnce class in $L$ to be an equivalence class in $N$, we need, as before: $$x \sim y \Rightarrow f(x) \sim f(y).$$ Or: $$x-y \in L' \Rightarrow f(x) - f(y) \in N' \Leftrightarrow f(x - y) \in N'.$$ So it suffice to require that $$f(L') \subset N'.$$ Then, $f$ can be conveniently interpreted as a map of pairs: $$f:(L,L') \rightarrow (N,N').$$

To summarize, we state

Theorem. A linear operator $$f:(L,L') \rightarrow (N,N')$$ generates a quotient linear operator $$f:L/L' \rightarrow N/N'.$$

Considering the case of $N'=0$ give us an important

Corollary. A linear operator $$f:L \rightarrow N$$ generates a quotient linear operator $$f:L/L' \rightarrow N,$$ if $L' \subset \ker f$.

First isomorphism theorem. Let $M$ and $N$ be vector spaces (or modules), and let $$\varphi : L → N$$ be a linear operator (homomorphism). Then:

1. The kernel of $\varphi$ is a subspace (submodule) of $L$,
2. The image of $\varphi$ is a subspace (submodule) of $N$, and
3. The image of $\varphi$ is isomorphic to the quotient $L/ \ker(\varphi)$:

$$\text{im } \varphi \cong L/ \ker(\varphi).$$ In particular, if $\varphi$ is surjective then $N$ is isomorphic to $L/ \ker(\varphi)$.