Parametric surfaces

Let's represent the sphere as a parametric surface.

Start with the spherical coordinates:

$$x = r \cos {\theta} \sin {\varphi}$$

$$y = r \sin {\theta} \sin {\varphi}$$

$$z = \cos {\varphi}$$

where 2. $0 \leq {\theta} \leq 2{\pi}$ 3. $0 \leq {\varphi} \leq {\pi}$ 1. $r \geq 0$

This will be the domain of this function:

$$S: D(S) {\rightarrow} {\bf R}^3, D(S) \subset {\bf R}^3,$$

$$S'|_{(0, \theta, \varphi)} = 0.$$

To parametrize the sphere, $r = 1$, fixed. For

$$f: D(f) {\rightarrow} {\bf R}^3,$$

$$D(f) = \{ ( {\theta}, {\varphi} ): 0 \leq {\theta} \leq 2{\pi}, 0 \leq {\varphi} \leq {\pi} \}.$$

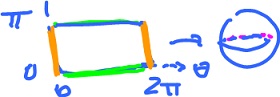
The image of $f$ is the unit sphere but the domain is a rectangle.

$$x = \cos {\theta} \sin {\varphi},$$

$$y = \sin {\theta} \sin {\varphi},$$

$$z = \cos {\varphi}.$$

(1) ${\rm Im}(f) \subset S( 0, 1 )$. How?

$( x, y, z ) \in S( 0, 1 )$ iff $x^2 + y^2 + z^2 = 1$ (distance to $0$ is $1$).

$$\begin{array}{} ( \cos {\theta} \sin {\varphi} )^2 + ( \sin {\theta} \sin {\varphi} )^2 + ( \cos {\varphi} )^2 &= \cos^2 {\theta} \sin^2 {\varphi} + \sin^2 {\theta} \sin^2 {\varphi} + \cos^2 {\varphi} \\ &= \sin^2 {\varphi} ( \cos^2 {\theta} + \sin^2 {\theta} ) + \cos^2 {\varphi} \\ &= \sin^2 {\varphi} + \cos^2 {\varphi} \\ &= 1. \end{array}$$

(3) $f( 0, {\varphi} ) = f ( 2{\pi}, {\varphi} )$, so we glue $( 0, {\varphi} )$ to $( 2{\pi}, {\varphi} )$ for each ${\varphi}$, so the left edge is glued to the right edge. The lower edge is $f( {\theta}, 0 ) = f ( {\theta}', 0 )$. "Image". Indeed:

$x = \cos {\theta} \sin {\varphi}$$

$f: y = \sin {\theta} \sin {\varphi}$$

$z = \cos {\varphi}$$

hence $f( {\theta}, 0 ) = ( 0, 0, 1 ) = f ( {\theta}', 0 )$.

So the points on the lower edge are glued together to a single point. The same holds for the upper edge.

(4) Find the best affine approximation of $f$ at $( 0, \frac{\pi}{2} )$ (i.e. find the tangent plane to the surface at a point).

$$\frac{\partial f_1}{\partial \theta} = - \sin {\theta} \sin {\varphi}, \frac{\partial f_1}{\partial \varphi} = \cos {\theta} \cos {\varphi}$$

$$\frac{\partial f_2}{\partial \theta} = \cos {\theta} \sin {\varphi}, \frac{\partial f_2}{\partial {\varphi}} = \sin {\theta} \cos {\varphi}$$

$$\frac{\partial f_3}{\partial {\theta}} = 0, \frac{\partial f_3}{\partial {\varphi}} = -\sin {\varphi},$$

plug in ${\theta} = 0$, ${\varphi} = \frac{\pi}{2}$:

$$f'( 0, \frac{\pi}{2} ) = \left| \begin{array}{} 0 & 0 \\ 1 & 0 \\ 0 & -1 \end{array} \right|$$

and

$$f(0, \frac{\pi}{2}) = \left| \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right|$$

Then

$$T( {\theta}, {\varphi} ) = \left| \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right| + \left| \begin{array}{} 0 & 0 \\ 1 & 0 \\ 0 & -1 \end{array} \right| \cdot ([ \theta, \varphi]^t - [0, \frac{\pi}{2} ] ^t)$$

See also

• Cylinder,
• Torus,
• Implicit Function Theorem.