Modelling with discrete vector fields and forms

Redirect to:

• ODEs

The $1$-dimensional case

Let's recall how we describe motion in dimension $1$. It is given by an ordinary differential equation (ODE): $$x'(t)=f(x(t)),$$ where $f:R \to R$ is continuous and $x:I \to R$ is differentiable on an open interval $I$. The equation has to be satisfied for all $t \in I$.

We can think of this ODE as a model for a fluid flow. Here $x$ is the position of a given particle as a function of time $t$ and $f(x)$ is the velocity of this particle (or any other) if it happens to be at point $x$.

How do we recast this problem in terms of differential forms?

The equation can be rewritten as $$\frac{dx}{dt} = f(x),$$ which turns into: $$dx=f(x)dt,$$ where $x$ is still a $0$-form, but $dx$ its exterior derivative, a $1$-form, and $dt$ the constant $1$-form.

Now what about the discrete case?

It supposed to be the same equation, with the same interpretations of its parts -- just on a grid.

But which grid? There are two: $t$ and $x$, time and space. Which one should be discrete? Or both?

Suppose we discretize time first. Then $x$ is simply a function of discrete variable. And so can $dx$, as a real valued $1$-form. But it can take any real value and, it follows, then that there can't be any grid for $x$!

The result is very simple: $$x(t_{n+1})-x(t_n)=f(x(t_n)).$$ It is known as a difference equation (DE). It can be written simply as: $$x_{n+1}=x_n+f(x_n).$$ It is an example of a discrete dynamical system.

Can we make both time and space discrete?

Yes, if you just limit yourself to forms with integer coefficients! One may call the result an integer-valued difference equation (IVDE). It is easy to verify that everything that we have done with real-valued discrete forms is fully applicable to the integer-valued forms (we don't divide!).

But do we really need to discretize space?

Consider the possibility that the velocity of the flow comes from measurements rather than from a theory. But we can measure the velocity only in finitely many different locations! How do we simulate motion of a particle then?

Let's assume that the velocity $f$ is only defined at the vertices of the grid for the $x$ variable. Suppose we have computed the next location of the particle: $$x_{n+1}=x(t_{n+1})=x(t_n)+f(x(t_n)).$$ Now, it is likely that this new location $x_{n+1}$ is in the middle of a cell $a$ and $f$ is undefined at $x_{n+1}$. Where do we go next?

There are two choices:

1. either "interpolate" $f$ to $x$ from the vertices of $a$ and compute the next location using this new function,
2. or "extrapolate" $x$ to the nearest vertex of $a$ and proceed from there.

If one wants to pre-compute $f$, the algebra is simple in either case:

1. for each cell $a=[u,v]$, let $f(\alpha u+(1-\alpha)v)=\alpha f(u)+(1-\alpha)f(v)$ for all $\alpha \in [0,1]$;
2. for each vertex $v$, replace $f(v)$ with $[f(v)+1/2]$.

The former case has produced a DE and the latter IVDE.

Both cases are important. In either,

• the equation itself is given by a $1$-form, real- or integer-valued, and
• its solution is a $0$-form, real- or integer-valued.

Modelling $1$-dimensional dynamical systems

Our difference equation $$x_{n+1}-x_n=f(x_n)$$ can be re-written as a dynamical system: $$x_{n+1}=F(x_n)$$ with $$F(x)=x+f(x).$$

Dynamical systems are known for exhibiting a complex behavior even with a simple choice of $F$:

One may study:

• limit behavior: $\lim_{n \to \infty} x_n=?$,
• fixed points: $x_{n+1}=x_n (F(x)=x)$,
• periodicity: $x_{n+P}=x_n$,
• chaos, etc.

Modelling is uncomplicated. For dimension $1$, one can simply use a calculator. Just enter a function and then repeatedly apply it. Excel is also good for that.

Exercise. Try $f(x)=rx(1-x)$ for $r=.5,1,2,3.3,3.5,4$. It is called the logistic map.

Of course, in the case of a IVDE both $x_n$ and $F$ are integer-valued and the dynamics is integer-valued too. As a result the complexity is diminished. In particular, the limit behavior of a particle can only be:

• infinite, or
• eventually reaching
  • a fixed point or
  • a periodic point.

What about higher dimensions?

Vector fields

Let's recall that a vector field is given if there is a vector attached to each point of the plane: $${\rm point} \mapsto {\rm vector}.$$ So, vector field is just a function $$f \colon {\bf R}^2 \rightarrow {\bf R}^2.$$

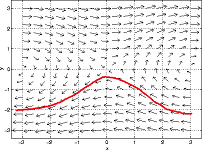
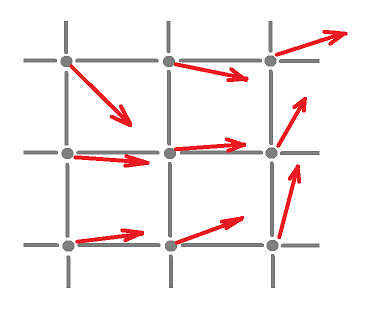
For example, the following vector field $$f=(f_x,f_y)$$ could be a velocity field of a flow:

One can think of vector fields as systems of ODEs: $$x'(t)=f_x(x(t),y(t)),$$ $$y'(t)=f_y(x(t),y(t)),$$ where $f_x,f_y:{\bf R}^2 \to {\bf R}$ are continuous and $x,y:I \to {\bf R}$ is differentiable on an open interval $I$. This is still a model for a fluid flow: $(x,y)$ is the position of a given particle as a function of time $t$ and $(f_x(x,y),f_y(x,y))$ is the velocity of this particle (or any other) if it happens to be at point $(x,y)$. A possible solution to this ODE is shown above.

How does this work with differential forms?

Same as before but twice: $$dx=f_x(x,y)dt,$$ $$dy=f_y(x,y)dt.$$ Here $x,y$ are $0$-forms, $dx,dy$ their exterior derivatives, $1$-forms, and $dt$ the constant $1$-form.

Now the discrete case.

Case 1. We discretize time first. Then $x,y$ is simply a function of discrete variable that can take any real value. The result is: $$x(t_{n+1})-x(t_n)=f_x(x(t_n),y(t_n)),$$ $$y(t_{n+1})-y(t_n)=f_y(x(t_n),y(t_n)).$$ These can be written simply as: $$x_{n+1}=x_n+f_x(x_n,y_n),$$ $$y_{n+1}=y_n+f_y(x_n,y_n).$$ This is a $2$-dimensional discrete dynamical system. In the vector notation: $$u_{n+1}=u_n+f(u_n).$$

Case 2. To make both time and space discrete we limit yourself to forms with integer coefficients.

For modelling the two cases are handled as follows:

1. either "interpolate" $f$ to $u_{n+1}=u_n+f(u_n)$ from the vertices of the cell and compute the next location using this new function,
2. or "extrapolate" $u_n$ to the nearest vertex of the cell and proceed from there.

Exercise. Find the formulas $f$ for both cases.

Discrete vector fields

Now, what is a discrete vector field?

The "vector field" for DE and IVDE, respectively, would look like that:

They correspond to $$f \colon {\bf Z}^2 \rightarrow {\bf R}^2$$ and $$f \colon {\bf Z}^2 \rightarrow {\bf Z}^2,$$ respectively.

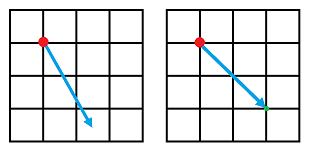
For the case of DE, the function $f$ will have to be extrapolated, as explained in the previous section, to a continuous vector field, just like the one above. The difference is that the solution isn't a curve but a sequence of points:

For the case of IVDE, $f$ is a discrete-valued vector field, the solution is a sequence of vertices.

There are other possible interpretations.

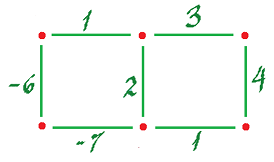
Sometimes our interest is a discrete vector field as a solution to a PDE, such as the Navier-Stokes equations. In that case, it is just a discrete $1$-form understood as a system of pipes:

A natural discretization of a vector field may be a "vector-valued" $0$-form (normally, $0$-form is scalar-valued), in the sense that there is a vector assigned to each $0$-cell:

For modelling of motion of a particle, however, one has to interpolate the vector field to the rest of the cells.

Also, what if one assigns the components of the vector to the adjacent edges?

.

Then this is just a $1$-form again!

Vector-valued differential forms

The "doubling" of our equation: $$dx=f_x(x,y)dt,$$ $$dy=f_y(x,y)dt,$$ will be awkward for higher dimensions. The vector notation is preferable. And we already have it for the discrete case: $$u_{n+1}-u_n=f(u_n),$$ where $u$ is any $2$-vector. Now we just need to adapt to the general case.

It should look like this: $$du=f(u)dt.$$ Here

• $f:{\bf R}^n \to {\bf R}^n$ is a vector function and
• $dt$ is still the constant $1$-form.

What is $u$? It's still a parametric curve $$u:[0,1] \to {\bf R}^n.$$ But we have its exterior derivative in the left-hand side! So $u$ should be some kind of $0$-form. Except it's vector-valued as a function?

That's why we need to define vector-valued forms. A $0$-form is understood in the simple, coordinate-wise fashion we have considered: $$u=(u_1,u_2,...,u_n)$$ with each $u_i$ a familiar, real-valued form. Now its exterior derivative is also just a vector of forms: $$du=(du_1,du_2,...,du_n),$$ and so are all vector-valued $1$-forms.