This site is being phased out.
Limits: part 2
This is a part of Calculus 1: course.
Contents
New Limits from Old
Follows the idea of making new functions from old.
How?
Algebraic operations $ +, -, \cdot, \div $
Example: $\underbrace{e^{x}}_{\text{continuous}} + \underbrace{x}_{\text{continuous}}$. Is it continuous?
Consider: $$ \lim_{x \to 0} e^{x} = 1, \;\;\; \lim_{x \to 0} x = 0$$
Thus $$ \lim_{x \to 0} (e^{x} + x) = 1 + 0 $$
Rule: The limit of the sum is equal to the sum of the limits.
Sidenote: $$ \sqrt{3 + 2} \neq \sqrt{3} + \sqrt{2} $$
Consider how the rule works numerically.
| $x$ | $e^{x}$ | $x$ | $e^{x} + x $ |
|---|---|---|---|
| $1$ | $e$ | $1$ | $ e + 1 $ |
| $\frac{1}{2}$ | $\sqrt{e}$ | $\frac{1}{2}$ | $\sqrt{e} + \frac{1}{2}$ |
| $\frac{1}{3}$ | $\sqrt[3]{e}$ | $\frac{1}{3}$ | $\sqrt[3]{e} + \frac{1}{3}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $0$ | $1$ | $0$ | $1 + 0 = 1$ |
(Also, difference, product and quotient lead to a similar table.)
Sum Rule: Suppose $\lim\limits_{x \to a} f(x) = L$, $\lim\limits_{x \to a} g(x)= M$ (this means that we assume both exist!). Then $\lim\limits_{x \to a} (f(x) + g(x)) = L + M. $
Which means that $\lim\limits_{x \to a} (f(x) + g(x))$ also exists.
Similarly, $$ \begin{aligned} \lim_{x \to a} (f(x) - g(x)) & = L - M \\ \lim_{x \to a} (f(x) \times g(x)) & = L \times M \\ \lim_{x \to a} (f(x) \div g(x)) & = L \div M \end{aligned} $$ (they all exist.)
Example: Does $\lim\limits_{x \to a} (f(x)+g(x))$ exist, even though $\lim\limits_{x \to a} f(x)$ and $\lim\limits_{x \to a} g(x)$ do not?
Can the addition of $f + g$ cancel the irregular behavior? Yes.
Solution: What if $g = -f$? Then $f + g = 0$, so $\lim\limits_{x \to a} (f + g) = 0$. It exists.
For example: Take $f(x) = \dfrac{1}{x}; a = 0$
The $\lim\limits_{x \to 0} \dfrac{1}{x}$ does not exist. Neither does, $\lim\limits_{x \to 0} \left(-\dfrac{1}{x}\right)$. But $$ \lim_{x \to 0} \left( \dfrac{1}{x} + \left(-\dfrac{1}{x} \right) \right) = \lim_{x \to 0} 0 = 0 $$
Theorem: If $\lim\limits_{x \to a} f(x)$ exist but $lim_{x \to a} g(x)$ does not, then $\lim\limits_{x \to a} (f(x) +g(x))$ does not exist.
Prove it!
Review Exercise
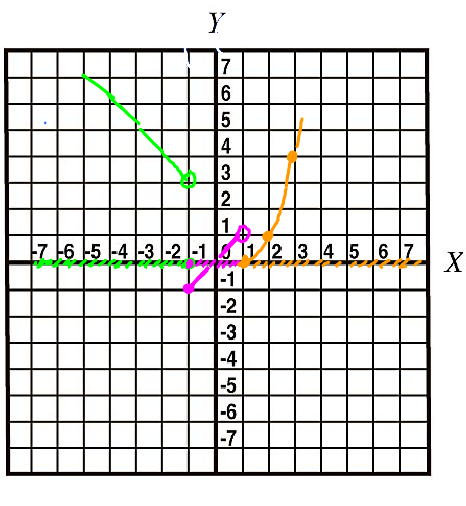
Plot the graph of: $$ f(x) = \begin{cases} 2 - x & \text{ if } x < -1 \\ x & \text{ if } -1 < x < 1 \\ (x - 1)^{2} & \text{ if } x >1 \end{cases} $$
$$ \begin{aligned} (1-1)^{2} & = 0 \\ (2-1)^{2} & = 1 \\ (3-1)^{2} & = 4 \end{aligned} $$
$\lim\limits_{x \to a} f(x)$ exists for all $a$ except $a = -1,1$
$$ \begin{aligned} \lim_{x \to -1^{-}} f(x) & = 3 \\ \lim_{x \to -1^{+}} f(x) & = -1 \\ \lim_{x \to 1^{-}} f(x) & = 1 \\ \lim_{x \to 1{+}} f(x) & = 0 \end{aligned} $$
The problem is about interpreting the graph in terms of limits.
Now, the other way around.
Exercise. From limits to graphs.
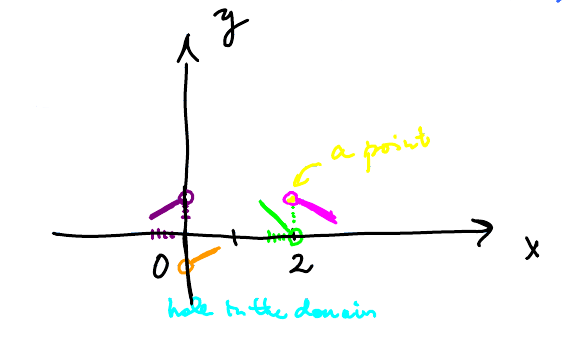
Given $$\begin{alignat}{3} \lim_{x \to 0^{-}} f(x) & = 1, & \quad \lim_{x \to 0^{+}} f(x) &= -1, & \quad f(0) & \text{undefined}, \\ \lim_{x \to 2^{-}} f(x) &= 0, &\quad \lim_{x \to 2^{+}} f(x) & = 1, &\quad f(2) &= 1 \end{alignat} $$
As $x \to 0^{-}, y \to 1$
As $x \to 0^{+}, y \to -1$
As $x\to 2^{-}, y \to 0$
As $x\to 2^{+}, y\to 1$
Just concentrate on the behavior of $f$ close to these prints.
Plot the graph of a possible $f$.
Algebraic Rules of Limits
How algebraic operations affect limits?
Assume that $\lim\limits_{x \to a} f(x)$ and $\lim\limits_{x \to a} g(x)$ both exist. Then $$ \begin{aligned} \lim_{x \to a} f(x) & = L \\ \lim_{x \to a} g(x) & = M \end{aligned} $$
Then, it is easy to conjecture that the limits on the left exist, first, and equal to the numbers on the right: $$ \begin{alignat}{3} \lim_{x \to a} (f(x) + g(x)) & = L + M & \quad &\text{ Sum} \\ \lim_{x \to a} (f(x) - g(x)) & = L - M & \quad &\text{Difference} \\ \lim_{x \to a} (cf(x)) & = cL & \quad &\text{ Constant} \\ \lim_{x \to a} (f(x)\cdot g(x)) & = L\cdot M & \quad &\text{ Product} \\ \lim_{x \to a} \left(\dfrac{f(x)}{g(x)}\right) & = \dfrac{L}{M} & \quad &\text{ Quotient, provided }M \ne 0 \\ \end{alignat} $$ In the last case, $g(x)$ can be 0 for some $x$.
Exercise: $f(x) = 1, g(x) = x, g(0) = 0$
Given a new function: $h(x) = \dfrac{f(x)}{g(x)}$, What is the domain of $h$?
They are the values of $x$ for which $h(x)$ makes sense. If $g(0) = 0$ then 0 is not the domain of $h(x) = f(x)/g(x)$.
Compute these limits:
$\lim_{x \to 0} \dfrac{f(x)}{g(x)} = \lim_{x \to 0}\dfrac{1}{x}$ does not exist, but $\lim_{x\to 1} \dfrac{f(x)}{g(x)} = 1$ does as $M = \lim_{x \to 1} x = 1 \neq 0$.
Example: $\lim_{x \to 2} 3 = 3$. Indeed, as $x\to 2, 3\to 3$ (where else?) as $y = 3$ does not go anywhere.
Example: Justify $\lim_{x \to 2} {(x)}=2$
Trivial. As $x \to 2$ as $x \to 2$ (where else?).
Example: $\lim{x \to 2} x^{2} = 2^{2} = 4$.
Justify : $f(x) = x^2$ is continuous at 2!
Very often: "$x \to 2$" is translated as $x = 2$, i/e., we evaluate the limit by substitution.
Substitution Property
Recall: If $f$ is continuous at $x = a$, then $\lim_{x \to a} f(x) = f(a)$. This is the definition of continuity. It's also called the direct substitution rule.
But what about $\lim_{x \to 1} e^{x^{2}}$? What if don't know (yet) that the function is continuous?
There is a better rule for this.
Substitution Rule. $$\lim_{x \to a} g(f(x)) = g(\lim_{x \to a} f(x)),$$
if $g$ is continuous at $y = \lim_{x \to a} f(x)$ (we assume that this limit exists!).
Example: Apply it. $\lim_{x \to 1} e^{x^{2}} = e^{\lim_{x \to 1} x^{2}} = e^{1^{2}} = e.$ This works because $e^{y}$ is continuous at $y = 1$.
The property is about compositions of functions:
$$ \xrightarrow[x]{} x^{2} \xrightarrow[y]{} e \xrightarrow[z]{} $$
Corollary If $f$ and $g$ are both continuous then $$\lim_{x \to a} g(f(x)) = g(f(a)).$$
Example $e^{y}$ and $x^{2}$ are continuous (everywhere). Then $$\lim_{x \to 1} e^{x^{2}} = e^{1^{2}} = e.$$
Example Justify this: $ \lim_{x \to 1} \sin \sqrt{x} = \sin \sqrt{1} = \sin 1.$
The substitution property applicable because $\sin y$ is continuous at $y = 1$ and $\sqrt{x}$ is continuous at 1.
Compare to $\lim\limits_{x \to 0} \sin \sqrt{x}$ which is undefined as is $\lim\limits_{x \to 0^{+}} \sin \sqrt{x}$
Corollary does not apply here because $\sqrt{x}$ is not continuous at 0, as we will see later.
Properties: (just choosing a specific $g$ in the substitution property)
- $\lim\limits_{x \to a} [f(x)]^{n} = [\lim\limits_{x \to a}f(x)]^{n}$, chose $g(y) = y^{n}$ here.
- $\lim\limits_{x \to a} \sqrt{f(x)} = \sqrt{\lim\limits_{x \to a} f(x)}$, if the right limit exist and is positive.
What if we end up with 0/0?
Example: Recall that $\lim\limits_{x \to 1} \dfrac{(x-1)^{2}}{x-1}$ or $\dfrac{0}{0}$
Sidenote: Informally, $\dfrac{1}{0} = \infty$. Observe that the numerator is non-zero here...
This expression, 0/0, is called and indeterminate, what does it mean?
We make no conclusions!
And we try something else, which usually is algebra.
$$ \lim \overset{\text{cancel}}{=} \lim_{x \to 1} (x - 1) \overset{\text{substitute}}{=} 1 - 1 = 0$$
Example: What should $\ast$ be in the limit $$\lim\limits_{x \to 1} \dfrac{\ast}{x-1} = 2$$ so that it makes sense?
Try this: $$ \begin{aligned} \lim_{x \to 2} \dfrac{(x-1)\cdot2}{x - 1} & = \lim_{x \to 2} 2 \\ &= 2 \end{aligned} $$
What if we replace 2 with 17? Compute...
In fact, this indeterminate expression, $\tfrac{0}{0}$, could be any number.
Further, can it be $\infty$?
Yes: $$\dfrac{0}{0} \gets \lim_{x \to 0} \dfrac{x - 1}{(x - 1)^{2}} = \lim_{x \to 1}\dfrac{1}{x - 1} = \infty ( = +\infty \text{ or } -\infty) $$
Example: $\lim\limits_{x \to 1} \dfrac{x^{2} -1}{x - 1} \rightarrow \dfrac{0}{0}$ If we mindlessly substitute, we get 0/0... What does it mean?
It means STOP! Erase everything and do algebra.
$$\begin{aligned} \lim\limits_{x \to 1} \dfrac{x^{2} -1}{x - 1} & = \lim_{x \to 1} \dfrac{(x - 1)(x+1)}{x-1} \\ & = \lim_{x \to 1} (x+1) \\ & = 2 \end{aligned} $$
Example: $\lim\limits_{x \to 0} \dfrac{\sqrt{x^{2} + 9} - 3}{x^{2}}$
Plug in: $\tfrac{\sqrt{0 + 9} - 3}{0} = \tfrac{0}{0}$. Not good.
Then do algebra, the purpose? To cancel the denominator.
Trick: Multiply by the "conjugate": $\sqrt{x^{2} + 9} + 3$.
The goal is to "rationalize" the numerator. It works because of the formula: $$ (a-b)(a+b) = a^{2} - b^{2} $$ Thus $$ \begin{aligned} \lim_{x \to 0} \dfrac{\sqrt{x^{2} + 9} - 3}{x^{2}} & = \lim_{x \to 0} \dfrac{(\sqrt{x^{2} + 9} - 3)\cdot (\sqrt{x^{2} + 9} + 3)}{x^{2}\cdot (\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{(x^{2} + 9) - 3^{2}}{x^{2}(\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{x^{2}}{x^{2}(\sqrt{x^{2} + 9} + 3)} \\ & = \lim_{x \to 0} \dfrac{1}{\sqrt{x^{2} + 9} + 3} \\ & = \dfrac{1}{\sqrt{0 + 9} + 3} = \dfrac{1}{6} \end{aligned} $$ Still $\dfrac{0}{0}$, but not after canceling. QR applies because the limit in the denominator exists and is not 0.
How to apply the rules
Be careful about applying the rules. For example, if you apply the sum rule: $$ \lim_{x \to a} (f(x) +g(x)) \overset{\text{SR}}{=} \lim_{x \to a} (f(x) + \lim_{x \to a} (g(x),$$ wrong, unless both limits exist.
Also, "DNE" is not a number: $ \text{DNE} + 5$ is meaningless.
Rule: Don't do algebra with "DNE".
Possible outcomes of limits: $$ \lim = \begin{cases} L, \text{ number } & \rightarrow \text{ algebra } \\ \infty, +\infty, -\infty & \rightarrow \text{ some algebra: } \infty + \infty = \infty \\ \text{DNE} & \rightarrow \text{ no algebra} \end{cases}$$
It;s similar to what we observe when we deal with functions (no limits). Recall:
Functions : 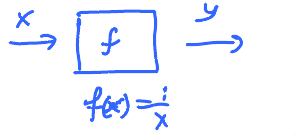
There may be nothing here as the output.
In particular, $$\left.\begin{aligned} \lim_{x \to a} f(x) &- \lim_{x \to a} f(x) \\ & \dfrac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} f(x)} \end{aligned} \right\} \qquad \text{Do nothing}$$ Unless you know the limits exist.
Review Exercise
$$\lim_{x \to -3^{-}} \dfrac{x+2}{x+3} = ?$$
Numerically: $$\begin{aligned} x & = 4, -3.5, -3.1, -3.01, \ldots \\ y & = \ldots, \ldots, \ldots, \ldots, \ldots, \to +\infty \end{aligned} $$
Incomplete... (same problem with plotting)
Solution: (algebraical)
$$ \begin{aligned} \lim_{x \to -3^{-}} (x + 2) & = -3 + 2 = -1 \quad \text{Since } x+2 \text{ is continuous.} \\ \lim_{x \to -3^{-}} (x + 3) & = -3 + 3 = 0 \quad \text{Since } x+3 \text{ is continuous.} \end{aligned} $$
Observe: Since limit of domain is 0, the QR (above) does not apply. But, $\lim$ of the numerator is $0$! Therefore the limit of the quotient is infinite.
Question: Which infinity? $$ \lim = +\infty \text { or } \lim = -\infty $$
$x \to -3^{-}$ means $x < -3$ and close to -3. If $x$ is like this, what is the sign of $f(x) = \dfrac{x+2}{x+3}$? If $$ \begin{aligned} x + 2 & < 0 \\ x + 3 & < 0 \end{aligned} $$ So $f(x) >0$
Answer: $\lim\limits_{x \to -3^{-}} \dfrac{x+2}{x+3} = +\infty$
Continue to Limits: part 3.