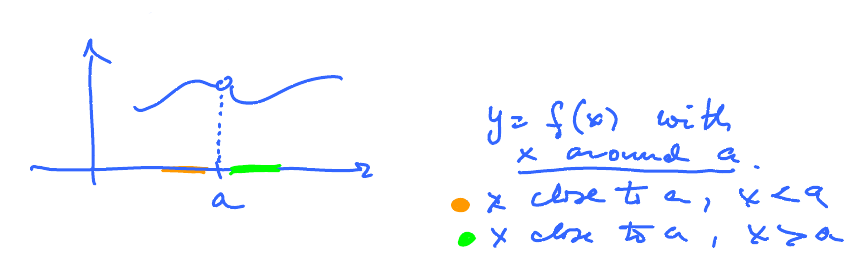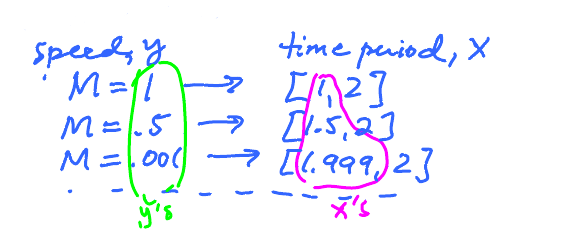This site is being phased out.
Limits: part 3
This is a part of Calculus 1: course.
Contents
How to tell limits that exist from limits that do not
Shortcut: All limit laws apply equally to one sided limits, $\lim\limits_{x \to a}$ replaced with $\lim\limits_{x \to a^{+}}$ (or $\lim\limits_{x \to a^{-}}$).
Example: $$ \lim_{x \to a^{+}} (f(x)+ g(x)) = \lim_{x \to a^{+}} f(x) + \lim_{x \to a^{+}} g(x) $$
Sum Rule applies provided these two limits exist. Same for DR, PR, QR, SR.
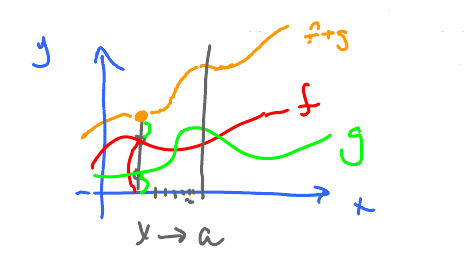
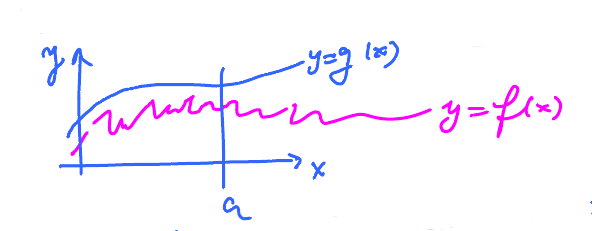
Example: Suppose we have the graphs of $f,g$ and we are interested in the limit of the sum.
The graph of $f + g$ is not very revealing. Let's try numbers instead.
Limit exists when:
$y$ approaches $L$ (some number or $\infty$), as $x$ approaches $a$ from both directions. Like this: $$ x \to 0: x = 1, -1, \dfrac{1}{2}, -\dfrac{1}{2}, \dfrac{1}{3}, -\dfrac{1}{3}, \ldots$$
We can break this into two: $$\begin{aligned} x &\to 0^{+}: x = 1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \ldots \\ x &\to 0^{-}: x = 1, -\dfrac{1}{2}, -\dfrac{1}{3}, -\dfrac{1}{4}, \ldots \end{aligned} $$
While $x$ has to approach $a$ from both sides, it's possible that there is nothing on one of the sides of $L$...
So, to evaluate $\lim\limits_{x \to a}$, we need to evaluate $\lim\limits_{x \to a^{-}}$ and $\lim\limits_{x \to a^{+}}$
Theorem: The limit $\lim\limits_{x \to a} f(x) = L$ exists if and only if $$ \lim_{x \to a^{-}} f(x) = \lim_{x \to a^{+}} f(x).$$
The last equation is to be understood as: both limits exist and they are equal to each other.
We need "equal", why?
Example:
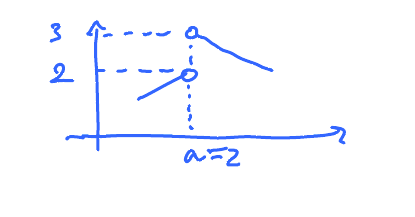 $$ \begin{aligned}
\lim_{x \to 2^{-}} f(x) &= 2 \\
\lim_{x \to 2^{+}} f(x) &= 3
\end{aligned} $$
$$ \begin{aligned}
\lim_{x \to 2^{-}} f(x) &= 2 \\
\lim_{x \to 2^{+}} f(x) &= 3
\end{aligned} $$
As $x\to 2$, $y\to 2$ or $y \to 3$. So, $y$ is not approaching a single value; we have two trends, not a single trend.
So $\lim\limits_{x \to 2} f(x)$ DNE.
Side-note: For functions of two variables, things are much more complicated in this respect because there are infinitely many directions from which one can approach a point...
Example: What is the $\lim\limits_{x \to a} f(x)$
We compare $\lim\limits_{x\to a^{-}} f(x)$ and $\lim\limits_{x \to a^{+}} f(x)$. Both exist and are equal to each other.
Example: $$ f(x) = \begin{cases} x & \text{ if } x < 1 \text{ (left, orange)}\\ x^{2} & \text{ if } x > 1 \text{ (right, green)} \end{cases} $$ Find $\lim\limits_{x \to a} f(x)$.
As $x\to 1$ and $x < 1$, we have $f(x) = x$. Then substitute that:
- Left limit
- $\lim\limits_{x \to 1^{-}} f(x) = \lim\limits_{x \to 1^{-}} x = 1.$
As $x\to 1$ and $x > 1$, we have $f(x) = x^{2}$. Then substitute that:
- Right limit
- $\lim\limits_{x \to 1^{+}} f(x) = \lim\limits_{x \to 1^{+}} x^{2} = 1^{2} = 1.$
So both limits exist and are equal. Then by the theorem, $\lim\limits_{x \to 1} f(x)$ exists, and it is equal to 1.
Review exercise
Compute the limit (specify the rules you apply): $$ \lim_{h \to 0} \dfrac{(2 + h)^{3} - 8}{h}.$$
Need algebra because $\tfrac{0}{0}$, if we plug in the value of the limit.
Using algebra to cancel the denominator.
We expand what's in parentheses:
$$ \begin{aligned} (2+h)^{3} & \neq 2^{3} + h^{3} \\ (2+h)^{2} & = 2^{2} + 2\cdot 2h + h^{2} \neq 2^{2} + h^{3} \end{aligned} $$
Recall: $$\begin{aligned} (a + b)^{3} & = (a + b)(a + b)(a + b) \\ & = (a^{2} + 2ab + b^{2})(a + b) \\ & = a^{3} + 3a^{2} b + 3a b^{2} + b^{3} \end{aligned} $$
Therefore $$\begin{aligned} \dfrac{(2+h)^{3} - 8}{h} &= \dfrac{2^{3} + 3\cdot 2^{2}\cdot h + 3\cdot 2\cdot h^{2} + h^{3} - 8}{h} \\ & = \dfrac{12h + 6h^{2} + h^{3}}{h} \\ & = 12 + 6h + h^{2} \to 12 \text{ as } h \to 0 \end{aligned} $$
Comparison of functions and their limits
We assume they exist...
Idea: Compare functions, that helps to compare their limits.
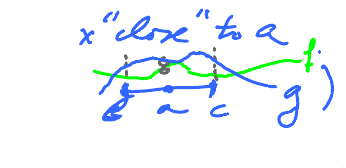
Consider that $f(x) < g(x)$ for all $x$ then $\lim\limits_{x \to a} f(x) \leq \lim\limits_{x \to a} g(x)$. (easy conjecture)
Theorem (Limit comparison). Suppose $f(x) \leq g(x)$ for all $x$ "close" to $a$ (i.e., for all $x $in $(b,a)$ and $(a,c)$). Suppose $\lim\limits_{x \to a} f(x), \lim\limits_{x\to a} g(x)$ exist. (Translation: These are numbers!) Then $$ \lim_{x \to a} f(x) \leq \lim_{x \to a} g(x). $$
Example: $$ f(x)=x^{2}, \quad g(x) = x^{2} + \underbrace{| \sin e^{x} |^{3}}_{\text{4 functions}} $$
We get $$ \begin{aligned} \lim_{x \to 1} f(x) & = 1^{2} = 1, \\ \lim_{x \to 1} g(x) & = \text{? I am interested in an estimate, a bound.} \end{aligned}$$
Notice something about $|\sin e^{x}|^{3}$: $$|\sin x| \leq 1,$$ so
- $0 \leq |\sin e^{x}|^{3} \leq 1 $
- Now $g$ is continuous, so $\lim\limits_{x \to 1} g(x)$ exists.
Estimate this limit: $$ \underbrace{1 + 0}_{1} < \lim_{x \to 1} g(x) \leq \underbrace{1 + 1}_{2} $$
Answer: Between 1 & 2
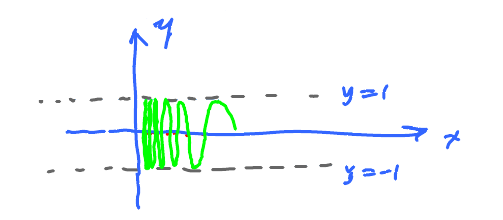
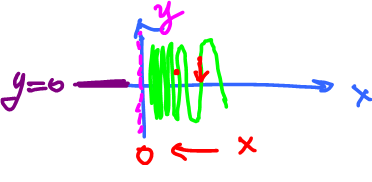
Example. Let $h(x) = \sin \dfrac{1}{x}$, with domain $(-\infty,0) \cup (0,\infty)$
Find $\lim\limits_{x \to 0} h(x)$.
Consider: $$\begin{aligned} -1 & \leq \sin x \leq 1 \\ -1 & \leq \sin \dfrac{1}{x} \leq 1 \end{aligned} $$
As $x \to 0, \tfrac{1}{x} \to \infty$. Now $\sin \pi k = 0$ for integer $k$, so $\sin \tfrac{1}{x} = 0$ for $x = \tfrac{1}{\pi k}$, where $k$ is an integer. Similarly, there are infinitely many values of $x$ with $\sin x=1, -1$etc. So, the limit does not exist.
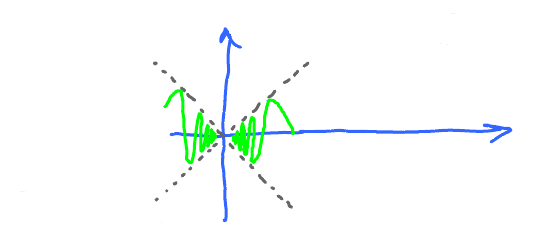
Example: Next, let $h(x) = x \sin \tfrac{1}{x} $.
Still holds: $$ x \sin \dfrac{1}{x} = 0 $$ for $x = \tfrac{1}{\pi k}$ and $k = 1, 2, \ldots $
In either case, there are infinitely many oscillations.
But here the swing dies down as it get close to 0.
It follows: $$ \lim_{x \to 0} x \sin \dfrac{1}{x} = 0.$$
Why the oscillations don't matter in this case? The graph of $h$ is between the two diagonals; and these diagonals meet at 0. So, $h(x)$ has no where else to go but 0. Here how $h$ is "squeezed" between two functions:
- $ –x \leq h(x) \leq x$ for $x > 0 $
- $\lim\limits_{x \to 0} –x = 0$
- $\lim\limits_{x \to 0} x = 0$
- $0 = 0$, equal limits!
So, $h$ is "sandwiched" between two functions that approach the same value as $x$ approaches 0. Then, $h$ approaches that value as $x$ approaches 0. This is the "squeeze theorem", or "sandwich theorem", or "theorem about two policemen", etc.
Theorem (The squeeze theorem). Suppose $$f(x) \leq h(x) \leq g(x),$$ for all $x$ close to $a$. Suppose the limits of $f$ and $g$ at $x = a$, $\lim\limits_{x \to a} f(x)$ and $\lim\limits_{x \to a} g(x)$,
- exist and
- are equal to each other.
Then, $\lim\limits_{x \to a} h(x)$ exists and equal to that number.
Both conditions are to be verified.
Example: Consider $h(x) = \sin \tfrac{1}{x}$, squeeze it: $$-1 \leq \sin \tfrac{1}{x} \leq 1$$ The limits of both left and right exists, of course, but: $$ \underbrace{\lim_{x \to 0} f(x) = 1}_{f(x)} \neq \underbrace{\lim_{x\to 0} g(x) = -1}_{g(x)} $$
The limits are not equal, so the theorem isn't applicable.
Conjecture: the limit does not exist. Prove that by other means.
As $x \to a$ what does $y = \sin \tfrac{1}{x}$ approach? No single value.
Need the "precise definition" of limit for the proof...
Precise definition of limit
Back to the spacecraft landing. Again question: How soft was the landing?
This time we realize: the question means different things to different people.
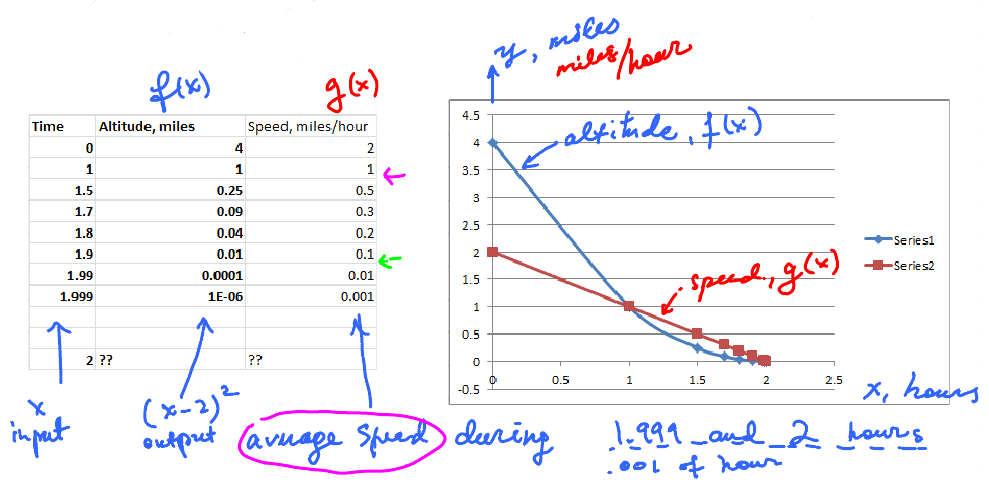
Recall our approach. We compute the average speed for several values of the altitude: how fast, on average, the module was moving between now and the time of landing. Plot altitude and speed (right). This is the data:
Now, hypothetically,
- Landing gear people came: "satisfactory" speed is 7m/h.
- Question: Was it soft? Find the appropriate row in the table.
- Answer: Average speed during the last 5hr was 5m/h. Yes, soft.
- Wiring people came. "Satisfactory" speed is .15m/h.
- Go to the table again, find the row, answer.
- Answer: average speed during the last .001h was .01 m/h. Yes!
- Equipment people came: they have another standard for speed for soft landing. Too many times happened, so...
Find a rule for answering these questions once and for all: $$ \begin{aligned} \text{Max speed allowed} & \to \text{ time period during which the average speed } \leq \text{ that} \\ \text{Q.} & \to \text{A.} \end{aligned} $$
How? We have the average speed as a function of time. $$ g(x) = \dfrac{(x-2)^{2}}{2-x},$$ where $x$ is the time and $x \neq 2$.
Problem: Given $M$, the max speed allowed, find $T$, time, so that for all $x$ in $[T,2], g(x) \leq M$.
Simplifying $g(x) = 2-x$ for $x = 2$, compare $g(T)$ and $M$. Find $T$ such that $$\begin{aligned} g(T) & \leq M \\ 2 - T & \leq M \\ \Rightarrow T & \geq 2 - M \end{aligned} $$
For the example above, look at the data:
Is there a limit? Looks like it...
as $T \to 2$, $M \to 0$.
So, there is always an answer, no matter how low the allowed speed is.
To summarize:.
The speed $y$ is the output of $g$. Now, we want it to be close enough to certain value of $y$ (it's 0 here) and we can ensure that by choosing the input of $g$ close enough to a certain value of $x$ (it's 2 here).
So, we have this. Limit $$y \to L \text{ as }x \to a$$ is interpreted as:
"We can make $y$ as close to $L$ as we like by making $x$ close enough to $a$."
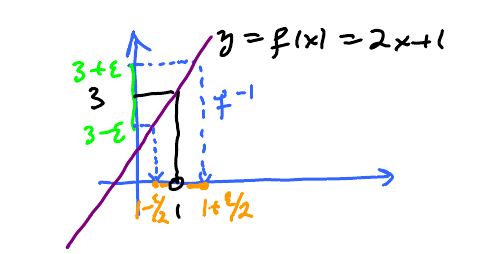
Example
Let's consider a simpler, mathematical, example.
- $f(x) = 2x+1$, $\lim\limits_{x \to 1} f(x) = 3$.
or
- $y \to 3$ as $x \to 1$.
To get started, let's make sure $y$ is within .5 from 3, how? We have no control over the output, $y$; we can only control the input, $x$. Let's make $x$ close enough to 1.
We need: $$ \begin{aligned} 2.5 & < y < 3.5 \\ 2.5 & < f(x) < 3.5 \end{aligned} $$ How? Choose (guess) this: $$ \begin{aligned} 0.9 & < x < 1.1 \\ \Rightarrow 1.8 & < 2x < 2.2 \\ \therefore 2.8 & < 2x+1 < 3.2 \end{aligned} $$ Yes, satisfied.
Now what if we look at 2.5 and 3.5 instead: $$ \underbrace{f(a)}_{2.5} \leq f(x) \leq \underbrace{f(b)}_{3.5} $$
Find $a$ and $b$ such that: $$ \begin{alignat}{2} f(a) & = 2.5 & \quad f(b) & = 3.5 \\ 2a + 1 &= 2.5 & \quad 2b+1 &= 3.5 \\ 2a &= 1.5 & \quad 2b &= 2.5 \\ a &=0.75 & \quad b&= 1.25 \end{alignat} $$
Answer: $[0.75,1.25]$
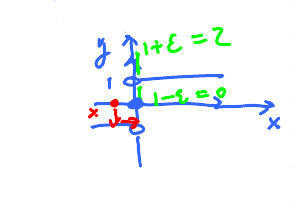
OK, what if we want it to be within not .5 but 0.3, 0.1, 0.001 etc from 3?
General solution:
- Given $\epsilon$ = how close is $y$ to 3.
- Find $\delta$ = how close is $x$ to 1.
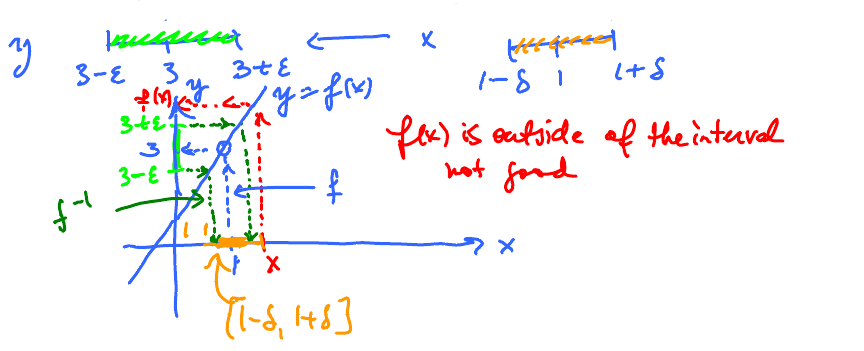
This is what we want: $$ 3- \epsilon < 2x + 1 < 3 + \epsilon$$ We achieve that by choosing $x$ such that: $$ 1 - \delta < x < 1 + \delta $$
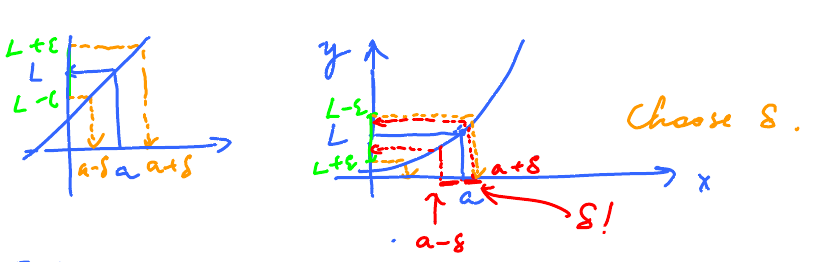
Given this, find that, below. Given a green interval around 3, find an orange interval around 1 that is taken to the green interval by $f$.
Observe that, in red, $f(x)$ is outside of the green interval. Not good. But the orange interval is all OK.
Algebraically $$ \begin{aligned} 3-2 & < 2x-1 < 3 + \epsilon \\ 1 - \delta & < x < 1 + \delta \end{aligned} $$ Need to explain how...
Recall, $y$ is supposed to be within $\epsilon$ from 3 (recall $(f(x) = 2x+1, a = 1, L = 3$). Goal: Find an interval on the $x$-axis so that all $x$'s in the interval go into $(3 - \epsilon, 3 + \epsilon)$ under $f$.
Solution: look at preimage of this interval, what are $f^{-1}(3 - \epsilon)$, $f^{-1}(3 + \epsilon)$?
Now, since $y= 2x + 1$, we need to solve: $$ \begin{aligned} y - 1 &= 2x \\ \dfrac{y-1}{2} = x \end{aligned}$$ So $$ f^{-1}(y) = \dfrac{y-1}{2} $$
$$ \begin{aligned} f^{-1}(3 - \epsilon) & = \dfrac{3 - \epsilon - 1}{2} = \dfrac{2 - \epsilon}{2} = \dfrac{1 - \epsilon}{2} \\ f^{-1}(3 + \epsilon) & = \dfrac{3 + \epsilon - 1}{2} = \dfrac{2 + \epsilon}{2} = \dfrac{1 + \epsilon}{2} \end{aligned} $$
Then our interval is $(1 - \tfrac{\epsilon}{2}, 1 + \tfrac{\epsilon}{2})$ or $(1 - \delta, 1 + \delta)$.
For every $\epsilon > 0$, we've found $\delta(=\tfrac{\epsilon}{2})$ such that if $x$ is in $(1 - \delta, 1 + \delta)$ then $y$ is in $(3 - \epsilon, 3 + \epsilon)$. And this is supposed to mean that $\lim\limits_{x \to 1} f(x) = 3$!
To make this more compact, rewrite by transitioning from intervals to inequalities:
- $x$ is in $(1 - \delta, 1 + \delta)$, or
- the distance from $x$ to 1 is less than $\delta$, or
- $|x - 1| < \delta$.
Similarly,
- $y$ is within $\epsilon$ from 3, or
- $ |y - 3| < \epsilon$.
Re-write: for every $\epsilon > 0$ we've found $\delta > 0$ such that if $$ | x - \underbrace{1}_{a} | < \underbrace{\delta}_{\delta = \dfrac{\epsilon}{2}}$$ then $$ | \underbrace{f(x)}_{y} - \underbrace{3}_{L}| < \epsilon. $$
Definition: $\lim\limits_{x \to a} f(x) = L$ if for every $\epsilon > 0$ there $\delta > 0$ such that if $ 0 < |x - a| < \delta$ then $|f(x) – L| < \epsilon$.
This is the infamous $\epsilon - \delta$ definition!
How to apply the definition
Typically, given $f, a, L$, find $\delta$ as a function of $\epsilon$.
Example: $f(x)= -3x – 2 , a = 2 , L = -4$. Find $f$ as a function of $\epsilon$ such that $$ |x - 2| < \delta \Rightarrow |\underbrace{-3x + 2}_{y} - (-4)| < \epsilon $$
Plan.
- Stage 1 : Find $\delta$.
- Stage 2: Prove that it satisfies the definition.
Stage 1.
Consider what we want: $$|x - 2| < \delta \overset{?}{\Rightarrow} |– 3x +6| < \epsilon. $$ What do these two have in common? To see it, try to turn $|x - 2|$ into $|-3x + 6|$.
Multiply $x-2$ by 3, then $$ \begin{aligned}3 |x - 2| &= |3(x - 2)| \\& = |3x - 6| \\& = |(-1)(3x-6)| = |-3x + 6|\end{aligned} $$ Rewrite $$ |x -2| < \delta \overset{?}{\Rightarrow} 3|x - 2| < \epsilon $$ Rewrite $$ |x - 2 < \delta \overset{?}{\Rightarrow} |x - 2| < \tfrac{\epsilon}{3}$$ Choose $\delta = \tfrac{\epsilon}{3} > 0$ (a function of $\epsilon$).
Stage 2. Prove that $\delta$ satisfies the definition.
Start with $$|x - 2| < \delta = \tfrac{\epsilon}{3}$$ and work your way toward $|-3x + 6) < \epsilon|$.
Multiply by 3 $$\begin{aligned}3|x - 2| & < \epsilon \\|3x - 6| & < \epsilon \\|-3x + 6| & < \epsilon \\|-3x + 2 –(-4)| & < \epsilon\end{aligned}$$ Done
Example. Prove $\lim\limits_{x \to 0} x^{2} = 0$
Here $$ f(x) = x^{2}, a = 0, L = 0.$$
Copy the definition and substitute these specifics.
For every $\epsilon > 0$, find $\delta > 0$ such that $$ |x - 0| < \delta \Rightarrow |x^{2} - 0| < \epsilon.$$ Re-write $$\begin{aligned} |x| < \delta & \overset{?}{\Rightarrow} |x^{2}| < \epsilon \\ & \sqrt{|x^{2}|} < \sqrt{\epsilon} \\ & \sqrt{|x|^{2}} < \sqrt{\epsilon} \\ |x| < \delta & \overset{?}{\Rightarrow} |x| < \sqrt{\epsilon} \end{aligned} $$ Choose $\delta = \sqrt{\epsilon}$. (This is stage 1!)
Graphical illustration of the definition:
Another example
Compute the limit by using the precise definition.
$\lim\limits_{x \to \underbrace{-1.5}_{a}} \underbrace{\tfrac{9 - 4x^{2}}{3 + 2x}}_{f(x)} = \underbrace{6}_{L} (\leadsto \tfrac{0}{0}).$
Plugging -1.5 give us an indeterminate expression. So, let's replace $f(x)$ with simpler one, equal to this for all $x \neq -1.5$. Some algebra: $$ \begin{aligned} \dfrac{9 - 4x^{2}}{3 + 2x} &= \dfrac{3^{2} - (2x)^{2}}{3 + 2x} \\ & = \dfrac{(3 + 2x)(3 - 2x)}{3 + 2x} \\ & = 3 -2x \end{aligned} $$ for all $x$ for which $3 + 2x \neq 0$, same as $x \neq 1.5$
Now, $f(x) = 3 - 2x$ is linear! Then the dependence of $\delta$ on $\epsilon$ is simple, in fact, linear.
- Stage 1
- $\delta = \tfrac{\epsilon}{2}$
- Stage 2
- Write the definition first
- For any $\epsilon > 0$ there is $\delta > 0$ such that$$ 0 < |x - a| < \delta $$ or $$\lim_{x \to a} f(x) = L$$
(We've found $\delta = \tfrac{\epsilon}{2}$) $$ 0 < | x - (-1.5)| < \dfrac{\epsilon}{2} \overset{?}{\Rightarrow} |3 - 2x - 6| < \epsilon$$ Verify this. $$ \begin{aligned} 0 < | x + 1.5| < \dfrac{\epsilon}{2} \overset{?}{\Rightarrow} & |-3 - 2x| < \epsilon \\ & | 2x + 3| < \epsilon \\ & | + 1.5 | < \epsilon \end{aligned} $$
Then, indeed, if $|x + 1.5| < \tfrac{\epsilon}{2}$ then $|-3 - 2x| < \epsilon$. The definition is satisfied.
This was "one day from the life of a math major".
Above: using the $\epsilon\cdot\delta$ definition to prove the existence of a limit.
Now: using the $\epsilon\cdot\delta$ definition to prove the non-existence of a limit.
Example. $$f(x) = \text{sign}(x) = \begin{cases} -1 & \text{ if } x < 0 \\ 0 & \text{ if } x = 0 \\ 1 & \text{ if } x >0 \end{cases}$$
Guess: $\lim\limits_{x \to 0} f(x)$ does not exist. So, we have to prove the opposite of the definition: there is no $L$ that satisfies the definition.
Or even less: let's just show that $L = 1$ is not the limit.
Idea: We can't come up with $\delta$ satisfying this condition for some $\epsilon > 0$.
Pick $\epsilon = 1$. Is there $\delta > 0$ such that: $$ 0 < |x - \overbrace{0}^{a}| < \delta \Rightarrow |\underbrace{\overbrace{\text{sign}(x)}^{f(x)} - \overbrace{1}^{L}| < \epsilon = 1}_{f(x) \text{ is within } (0,2)}$$
What $x$ would violate this? Any $x \leq 0$. If $x < 0$, then $f(x) = -1$ (outside of $(0,2)$).
No matter how close $x$ is to $a=0$.
The definition fails, so $L = 1$ is not the limit.
Exercise: What if $L = -1$, $L = 0$?