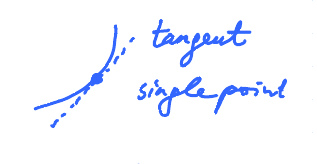This site is being phased out.
Limits: part 1
This is a part of Calculus 1: course.
Where limits come from
Problem: Suppose we have a landing module (maybe moon landing). What's its speed? (Observe there is no speedometer).
This is what we know: Altitude. At all times, except the end (maybe crash?).
Question: Was it a soft landing?
Solution: We'd approach the problem by computing the distance covered during the last:
- 2 mins
- 1 mins
- 0.5 mins
- etc
Then we use: $$ \text{average speed} = \dfrac{\text{distance}}{\text{time}}. $$
Review Exercise:
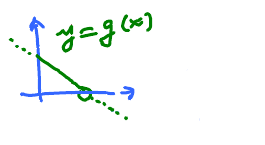
Plot the graph of the inverse of $y = f(x)$ plotted below:
- Draw the diagonal $y = x$,
- pick a few points on the graph of $f$ (we choose 4 points, call it $A$),
- plot a corresponding point for each of them:
- on the line through $A$ that is perpendicular to the diagonal,
- on the other side of the diagonal from $A$,
- some distance from the diagonal as $A$.
Red: graph of $f$ with $x,y$ coordinates Green: graph of $f$ with $x,y$ coordinates
Back to the landing problem...
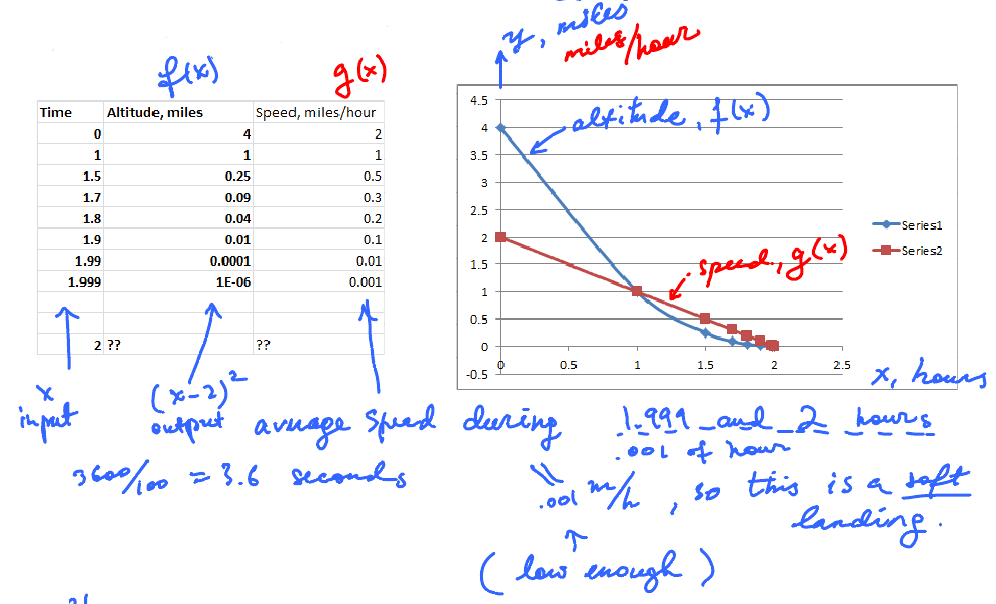
Compute the average speed for several values of the altitude: how fast, on average, the module was moving between now and the time of landing.
Plot the altitude and speed:
The data suggests that the landing was soft. Indeed the average speed is .001 m/h.
Further, from the point of view of physics we need an exact answer: What is the exact speed at the exact time $x = 2$?
Graph (red) suggests the answer is 0.
To justify, we need exact, complete data. Suppose we discover an exact formula. The altitude $y$ as a function of time, $x$, is $$ y=f(x) =(x-2)^{2};\;\; \text{ Domain } [0, 2)$$
Questions: First, are we landed when $x=2$? In other words, what is $f(2)$?
It's undefined! The reason is that 2 is excluded from the domain.
Instead, we ask:
Question: What is the trend close to the end of the decent?
Answer: 0, based on the graph.
Interpretation: $f(x)$ approaches 0 as $x$ approaches 2.
This is how we write this algebraically.
$$\lim_{x \to 2} f(x) = 0, $$ or $$\lim_{x \to 2} (x - 2)^{2} = 0, $$
How do we know the answer?
We found the answer by simply extending the domain to include 2, with the same formula.
Second: What is the speed at exactly $x=2$?
Say, the average speed at $x$ is $g(x)$. What is the formula for $g$?
Average speed,
$g(x) = \dfrac{f(x)}{2-x} \begin{cases} \gets \text{ distance covered} \\ \gets \text{ time passed} \end{cases}$
Plug in $x = 2$: $g(x) = \dfrac{(x-2)^{2}}{2-x}, \;\; x \neq 2$
Division by 2-x. So $x = 2$ is not in the domain, again.
Problem: $g(2)$ is undefined!
Solution: Consider the trend.
Question: As $x$ is approaching 2, what is $g(x)$ approaching?
Based on data, answer: 0
Do that algebraically: Rewrite $g$ as: $$ \begin{aligned} g(x) & = \dfrac{(x-2)^{2}}{2-x} \;\;\; (x\ne 2, \text{ a hidden restriction}) \\ & = 2-x \;\; \text{ for } x = 2 \text{ (domain)} \end{aligned} $$
Plot it:
Compute. We evaluate the limit of $ 2-x $, by letting $x=2$.
$$ \begin{aligned} \lim_{x\to 2} g(x) & = \lim_{x\to 2} (2 - x) \gets \text{ linear function }\\ & = 2-2 \\ & = 0 \end{aligned} $$ No mention anymore $x \neq 2$. This step is justified. It's clear because $2-x$ is such a simple function.
Limit as a trend
Example: Compute: $\lim\limits_{x\to 0} \dfrac{x^{2}}{x}$.
Observe: If plug in $x = 0$, $$ \dfrac{0^{2}}{0} = \dfrac{0}{0} $$
This is called "indeterminate expression".
Instead, cancel $x$ first, $$ \begin{aligned} \lim_{x \to 0} \dfrac{x^{2}}{x} & = \lim_{x\to 0} x \\ & = 0 \end{aligned} $$
Here $x\to 0$ means that $x$ approaches 0, never equal to 0. That's why canceling" $x$ is justified.
Example: Compute $\lim\limits_{x \to 0} \dfrac{x}{x^{2}}$.
We get $$ \lim_{x \to 0 } \dfrac{x}{x^{2}} = \lim_{x \to 0} \dfrac{1}{x} $$
Can't divide by $ x \neq 0 $ as $\dfrac{0}{0}$ is meaningless; can't plug in $x = 0 $.
So, back to the question: What's the trend?
Data:
| $x:$ | 1 | 0.1 | 0.01 | 0.001 | $\ldots$ | 0 |
|---|---|---|---|---|---|---|
| $y = \dfrac{1}{x}:$ | 1 | 10 | 100 | 1000 | $\ldots$ | $\infty$ |
We can see from the tables that as $x$ tends to zero, $y$ keeps growing and doesn't approach any number.
Answer: The limit does not exist. (it's an "infinite" limit, discussed later.)
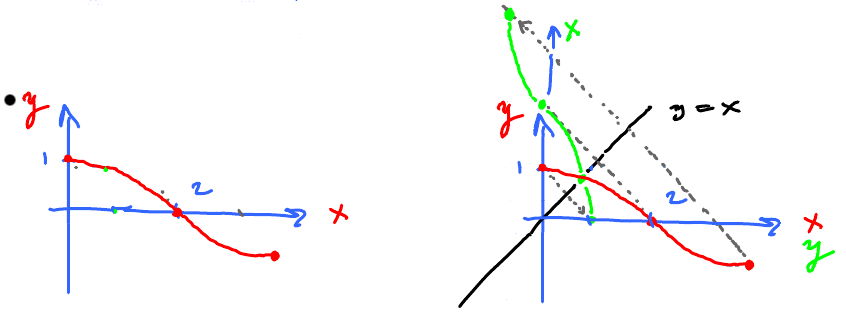
Example: Define the "sign function"
$$ f(x) = \begin{cases} -1 & \text{ if } x < 0 \\ 0 & \text{ if } x = 0 \\ 1 & \text{ if } x > 0 \end{cases} $$
Domain $f =(-\infty,\infty), f(0)= 0.$
Question: $\lim_{x \to 0} f(x) = $?
Try $$ \left.\begin{aligned} x & = 1, 0.1, 0.01, \ldots \\ f(x) & = 1, 1, 1, 1, \dots \end{aligned} \right\} \qquad \text{Right side} $$
Try $$ \left.\begin{aligned} x & = -1, -0.1, -0.01, \ldots \\ f(x) & = -1, -1, -1, -1, \dots \end{aligned} \right\} \qquad \text{Left side} $$
So,
- $ y = f(x)$ approaches (equal to) 1 as $x$ approaches 0 and $x > 0$.
- $ y = f(x)$ approaches (equal to) -1 as $x$ approaches 0 and $x < 0$.
Two good trends, but one too many...
Answer: The limit does not exist as there is no single trend!
- $\lim\limits_{x \to 0^{-}} f(x) = -1$, $x$ approaches 0 and $x < 0$.
- $\lim\limits_{x \to 0^{+}} f(x) = 1$, $x$ approaches 0 and $x > 0$.
To understand the behavior on each side separately, plot parts of the graph:
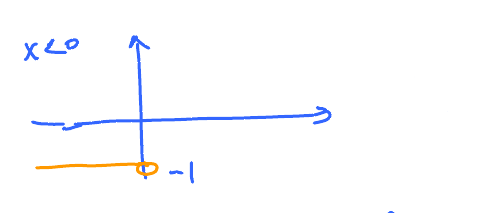
- Restrict the domain of $f$ to $(-\infty,0)$
- Notation: $0^{-}$
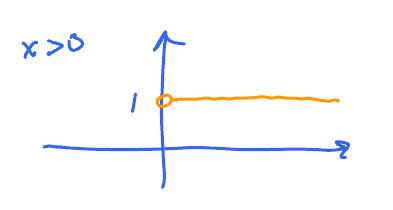
- Restrict the domain of $f$ to $(0,\infty)$
- Notation: $0^{+}$
Review Exercise:
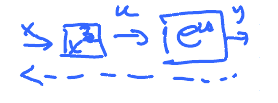
Find the inverse of $$ f(x) = e^{x^{3}}$$
NOTE: This is not $(e^{x})^{3}$
Method: Equation $y = e^{x^{3}}$, solve for $x$.
To get to $x$, we need to get rif of the exponent. To cancel it, apply its inverse to both sides
For $e^{x}$ its $\ln$: $$ \begin{aligned} \ln y & = \ln e^{x^{3}} \\ \ln y & = x^{3} \end{aligned} $$
Apply the inverse to get to $x$ $$ \begin{aligned} \sqrt[3]{\ln y} & = \sqrt[3]{x^{3}} \\ & = x \end{aligned} $$
Answer: $ f^{-1}(y) = \sqrt[3]{\ln y} $
This is how $x$ can approach 0:
$$ \begin{aligned}
1, & \dfrac{1}{2}, \dfrac{1}{3},\dfrac{1}{4}, \ldots \\
-1, & -\dfrac{1}{2}, -\dfrac{1}{3}, -\dfrac{1}{4}, \ldots \\
1, & -\dfrac{1}{2}, \dfrac{1}{3},-\dfrac{1}{4}, \dfrac{1}{5}, \dots
\end{aligned}
$$
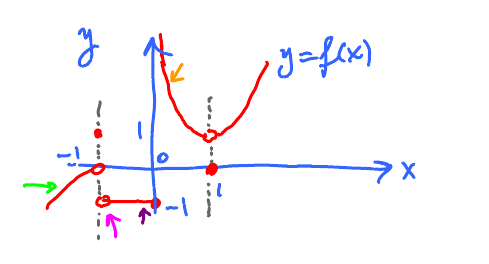
Look at the graph and describe the behavior using limits.
$ \lim\limits_{x \to -1} f(x)$ undefined because $$ \begin{aligned} \lim_{x \to -1^{-}} f(x) & = 0 \\ \lim_{x \to -1^{+}} f(x) & = -1 \end{aligned} $$
$\lim\limits_{x \to 0} f(x)$ undefined , because $$ \begin{aligned} \lim_{x \to 0^{-}} f(x) & = -1 \\ \lim_{x \to 0^{+}} f(x) & = \infty \\ \Rightarrow \lim_{x \to 1} f(x) & = 1 \end{aligned}$$ even though $ f(1)= 0 $.
Informal definition of limit
We write $\lim_{x \to a} f(x) = L$ if "the limit of $f(x)$ as $x$ approaches $a$ is $L$" (here $L$ is a number)
This means: Compute $y = f(x)$, for $x$ approaching $a$ and the trend is: $y$ approaches $L$.
Alternative notation: $$f(x) \longrightarrow L \text{as} x \longrightarrow a.$$ or $$\underset{\text{dependent}}{y} \longrightarrow L \text{as} \underset{\text{independent}}{x} \longrightarrow a.$$
Limits that are easy to compute are the ones that involve "continuous" functions.
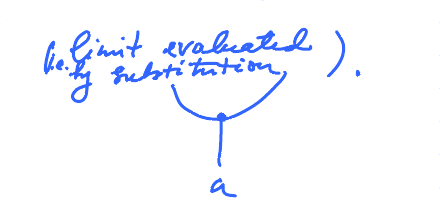
Definition: $y = f(x)$ is called continuous if $\lim\limits_{x \to a} f(x) = f(a)$, i.e. the limit is evaluated by substitution.
Example: Example above is not continuous.
- $f$ is undefined at $a$.
- $a$ is an end point of the domain of $f$.
Review Exercise
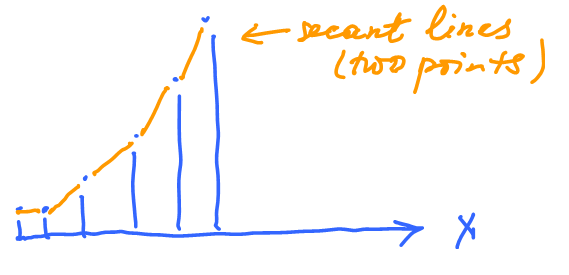
Estimate the tangent line of a function given numerically.
Use the secant lines, or average of two adjacent secant lines.
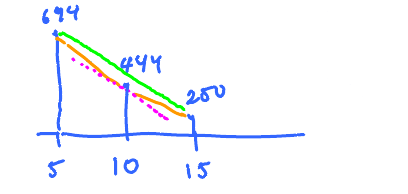
What is the slope at $x = 10$?
Slopes
- 1st Slope: $\dfrac{444 - 694}{5} = -50$
- 2nd Slope: $\dfrac{250 - 444}{5} = -38.8$
- Average: $ \dfrac{ -50 + (-38.8)}{2} = \dfrac{88.8}{2} = -44.4 $
- Use (b) or try another secant line (double)
Same: $ \dfrac{250 - 694}{10} $
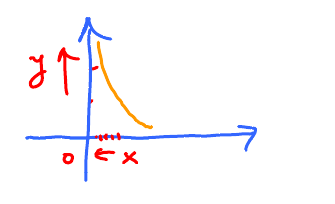
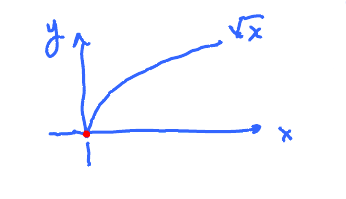
Example: $ f(x) = \sqrt{x} $, $f$ can not be continuous for $a < 0$
What about 0?
$f(0)= \sqrt{0} = 0$, defined, but $\lim\limits_{x \to 0} f(x) = \lim_{x \to 0} \sqrt{0}$ does not exist, because $x$ cannot approach 0 from the left. So $\sqrt{x}$ is not continuous at 0. There seems to be some kind of continuity at 0. What kind?
$\lim\limits_{x \to 0} f(x)$ does not exist. But $\lim\limits_{x \to 0^{+}} f(x)$ exists.
$$ \underbrace{\lim_{x \to 0^{+}} \sqrt{0} = \sqrt{0} = 0}_{\text{This is almost the definition for continuity.}} $$
So we say $\sqrt{x}$ is continuous from the right.
Example: $\dfrac{1}{x}$ is not continuous at 0.
Example: $\ln x$ is not continuous at 0.
Example: $\tan x$ is not continuous at $x$.
These are discontinuous outside their domains.
Example: The sign function is different:
Continuous: $$ \left. \begin{aligned} \text{polynomials} & \text{ for all } a \\ \sin x, \cos x & \text{ for all } a \end{aligned} \right\} $$
Which one does not belong? $$ \begin{aligned} \rightarrow \sqrt{x} & \text{ continuous for all } a > 0 \\ \rightarrow \dfrac{1}{x} & \text{ continuous for all } a \neq 0 \end{aligned} $$
Continuous on their domains:
Polynomials, trigonometric functions, rational functions, exponential functions, logarithms.
Example: $\lim\limits_{x \to 3} e^{x} = e^{3}$, so continuous at $x = 3$
Example: $\lim\limits_{x \to 5} \ln x = \ln 5 $. Use the fact that $\log$ is continuous on its domain. The expression makes sense, hence it's continuous. One can compute the limit by substitution.
On the other hand, $\lim\limits_{x \to -5} \ln x = \ln (-5)$ does not make sense. Hence it's not continuous, and the limit does not exist.
Continue to Limits: part 2.