Physics

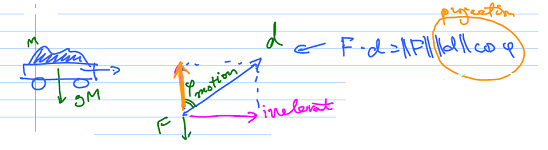
Suppose $F$ is a force. As we move, we perform work against the force. We can also consider the work performed by the force to move an object. We know that this number is $$W=Fd,$$ where $d$ is the distance moved.

As it is possible that we move with or against the force, we have to look at these two quantities as vectors. Then: $$W=F\cdot d.$$ Here $d$ is the displacement vector and $\cdot$ is the dot product. Indeed, this formula is justified by the fact the component of the force orthogonal to the direction of motion doesn't contribute to the amount of work performed, such as in this example of lifting without pulling (or pulling without lifting) this heavy cart:

More generally, the force may vary from location to location. We think of $F$ then as a vector field. Our motion may also be in various directions changing with time as we move along a parametric curve $C$.

This curve may be given by $$r=r(t)\in {\bf R}^n,t\in [a,b].$$

Along a "short" piece of this curve the above formula still applies but, as we add them together, we produce a line integral: $$W=\int _C F\cdot dr = \int _a^b F(r(t))\cdot r'(t)dt.$$ Here $F\cdot dr$ is a differential form of dimension $1$.

This is how we solve the "exactness problem". Given a continuous function $f$, it is exact if it's the derivative of something: $$f=F'.$$ To rephrase, the $1$-form $fdx$ is exact if it's the exterior derivative of some $0$-form: $$f=dF.$$ We simply define $$F(x)=\int _a ^x f(x)dx,x \in [a,b].$$

We consider closed and exact $1$-forms in ${\bf R}^2$.

All $1$-forms in ${\bf R}^2$ look like this: $$\varphi = f dx + g dy,$$ where $f=f(x,y),g=g(x,y)$ are functions of two variables.

Theorem: $\varphi = fdx + gdy$ is closed if and only if $g_x=f_y$.

Corollary. The Cauchy-Riemann equation $g_x=f_y$ is a necessary condition for a vector field $F=(f,g)$ to be conservative.

Question: When is $\varphi= fdx + gdy$ exact, $\varphi = d \psi$?

Here $\psi$ is simply a function of two variables. So, we conclude that $$\psi _x=f,\psi _y =g.$$ And further $$\psi =\int f(x,y)dx, \psi =\int g(x,y)dy.$$

Given a $1$-form $\varphi =fdx+gdy$ we construct a $0$-form $\psi$ with $d\psi =\varphi$ as a line integral. We fix a point $a \in {\bf R}^n$ and define $\psi$ as a function of $u=(x,y)$: $$\psi (u)=\int _C \varphi,$$ where $C$ is a path from $a$ to $u$.

Is this function well defined? To be well defined, $\psi$ should be independent of our choice of path $C$. There may be many paths from $a$ to a given $u$ and they all should produce the same value to be assigned to $\psi (u)$.

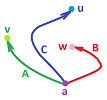
Suppose we have another path $C'$ from $a$ to $u$ that doesn't intersect $C$ except at the end points. Then we need to prove that $$\int _C \varphi = \int _{C'} \varphi.$$

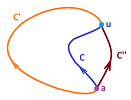
Recall that by paths we understand parametric curves (that we can integrate). The idea is to form a closed path from $a$ to $a$ from these two: $K=C \cup -C'$, where $-C'$ is $C$ parametrized in the opposite direction.

Then, on one hand, we compute $$\int _K \varphi =\int_C \varphi + \int _{-C'} \varphi = \int_C \varphi - \int _{C'} \varphi.$$ On the other hand $$\int _K \varphi = \int\int _D (g_x-f_y)dxdy ,$$ where $D$ is the region bounded by $K$, by Green's theorem. Therefore the integral is zero because the form $\varphi =fdx+gdy$ is closed. It follows then that $$\int_C \varphi - \int _{C'} \varphi =0.$$

Finally we differentiate the integral which is just a function: $$d\psi = \psi _x dx + \psi _y dy = fdx+gdy.$$ The result follows from the Fundamental Theorem of Calculus for parametric curves.

Theorem (Poincare Lemma). Every closed $1$-form in ${\bf R}^n$ is exact.

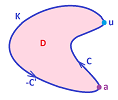
Example. Consider $$\theta = \frac{1}{x^2+y^2} (-ydx + xdy)$$ $$ = f dx + g dy.$$ This one is closed. But $\theta $ is not exact! (Proof long.) The domain is $R = {\bf R}^2 - \{(0,0)\}.$

Conclusion: It is not true that every closed $1$-form in ${\bf R}^2 - \{(0,0)\}$ is exact.

What makes the difference is the topology of the region $R$.