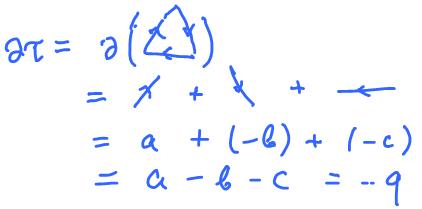Homology in dimension 2

Redirect to:

• Oriented chains

Start at Homology in dimension 1.

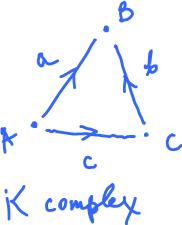
Recall that given a cell complex $K$, a $k$-chain is a "formal" linear combination of finitely many oriented $k$-cells, such as $3a + 5b - 17c$ with, typically, integer coefficients. Then the set of all $k$-chains $C_k(K)$ is an abelian group with respect to chain addition generated by the $k$-cells of $K$: $$C_k(K) = \left\{ \displaystyle\sum_i s_i \sigma_i \colon s_i \in {\bf Z}, \sigma_i {\rm \hspace{3pt} is \hspace{3pt} a \hspace{3pt}} k{\rm -cell \hspace{3pt} in \hspace{3pt}} K \right\}$$

In order to capture the topology of the cell complex we use the boundary operator.

The boundary of a vertex empty, so the boundary operator of a $0$-chain is $0$: $$\partial (A) = 0 {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} A \in C_0(K).$$

The boundary of a $1$-cell consists of its two end-points: $$\partial (a) = \partial (AB) = B - A {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} a = AB \in C_1(K),$$ extended to the whole chain complex by assuming that $\partial$ is a homomorphism (or a linear operator in the vector space case).

A chain is called a cycle if its boundary is $0$: $$Z_k(K) = {\rm ker}(\partial).$$

In the above example, we have: $$Z_1(K) = {\rm span}\{ q \},$$ where $$q = -a + b + c,$$ or, in the group case, $$Z_1(K) = .$$

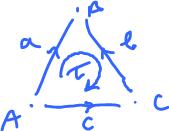
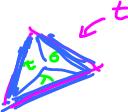
Adding a face to this triangle will patch the hole and, algebraically, make $q = -a + b + c$ homologous to $0$, i.e., it's the boundary of a surface. To make this idea algebraic we need to define the boundary operator for cells (and chains) of dimension $2$. The procedure for the $2$-cell in the new complex $L$ is illustrated below:

Here we first follow the chain around clockwise as indicated by its orientation writing the $1$-cells as they appear, and then interpret these $1$-cells in terms of the $1$-cells $a, b, c$, that we recorded in our cell complex $L$ (compare to boundary operator of simplicial complexes). It can be extended to the whole chain complex $C_2(L)$.

The conclusion: $q$ is indeed a boundary. We established this by solving this equation: $$u = \partial ( \alpha ) {\rm \hspace{3pt} over \hspace{3pt} all \hspace{3pt}} \alpha \in C_2(L).$$

It follows that $$H_1(L) = 0.$$

Definition. The $k$-boundary group of cell complex $K$ is the set of all boundaries of the $(k+1)$-chains in $K$, i.e., it's the image of the $(k+1)$-chain group: $$B_k(K) = \partial (C_{k+1}(K)).$$

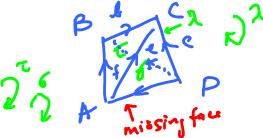
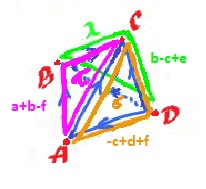
Let's consider another example. Suppose $K$ is a $3$-face pyramid (no bottom face):

• $\dim 0: A, B, C, D;$
• $\dim 1: a, b, c, d, e, f$;
• $\dim 2: \lambda, \sigma, \tau$.

Topology problem. Find all $1$-cycles that are boundaries of $2$-chains.

In other words, we need to compute the boundary group $B_1(K)$. This is what we know: $$\partial \lambda = a + b - f,$$ $$\partial \sigma = f - c + d,$$ $$\partial \tau = -c + e + b.$$

In the vector space environment, $$C_2(K) = {\bf R}^3, C_1(K) = {\bf R}^6,$$ so the boundary operator $$\partial \colon C_2(K) \rightarrow C_1(K)$$ is represented by a $6 \times 3$ matrix.

Exercise. (a) Without finding the matrix, what are the possible outcomes for the image of $\partial$? (b) Find the matrix of $\partial$.

Linear algebra problem. Find the image of the linear operator $\partial$.

We need to find all $u = \partial ( \alpha ), \alpha \in C_2(L)$. Suppose $$u = x\lambda + y\sigma + z\tau, {\rm \hspace{3pt} for \hspace{3pt} some \hspace{3pt}} x, y, z \in {\bf R}.$$

Then $$\begin{array}{l} \partial u &= x \partial \lambda + y \partial \sigma + z \partial \tau \\ &= x(a + b - f) + y(f - c + d) + z(-c + e + b) \\ &= xa + (x + z)b + (-y - z)c + yd + ze + (-x + y)f \end{array}$$

Or, $$\partial \colon [x,y,z] \rightarrow [x, x + z, -y - z, y, z, -x + y].$$

Is there a $1$-chain ($6$-vector) that's not here?

Let's try $a = [1, 0, 0, 0, 0, 0]$. Is this a boundary?

Compute: $$x = 1 \rightarrow z = -1, y = 1,$$ so, no!

What about $t = [1, 0, 0, 1, -1, 0]$? At the first sight it may seem that since $t$ is the boundary of the missing face, it's not a boundary in $K$. We can see why this is wrong by looking at the image on the right or, even better, we can just let algebra do the work.

From the equations, $$\begin{array}{} x = 1, \\ x + z = 0 \rightarrow z = -1, \\ -y - z = 0 \rightarrow y = 1, \\ y = 1, \\ z = -1, \\ -x + y = 0. \end{array}$$

So, $$t = \partial [1, 1, -1].$$

This is what we have to deal with: $$\begin{array}{} x_1 = x, \\ x_2 = x + z, \\ x_3 = -y - z, \\ x_4 = y, \\ x_5 = z, \\ x_6 = -x + y. \end{array}$$

To capture all possible vectors $[x_1, ..., x_6]$ we can treat $x, y$, and $z$ as parameters. Since $$\partial ([x,y,z]) = \partial (xa + yb + zc),$$ the image of $\partial$ is spanned by $$p = \partial (a) = [1, 1, 0, 0, 0, -1]$$ $$q = \partial (b) = [0, 0, -1, 1, 0, 1], $$ $$r = \partial (c) = [0, 1, -1, 0, 1, 0].$$

Next, by solving a homogeneous system of linear equations, we show that $p, q, r$, are linearly independent. Therefore, $\{p, q, r \}$ is a basis of $B_1(K)$.

A topological interpretation of this result is simple:

Exercise. Represent the torus as a cell complex with two $2$-cells, compute the boundary group $B_1(K)$ by solving a system of linear equations (as above).

Example. Compute the homology of sphere with membrane.

Cells of $K$:

• $2$-cells: $\mu, \sigma, \tau$,
• $1$-cells: $e$,
• $0$-cells: $A$.

Chain groups:

• $C_2(K) = {\rm span}\{\mu, \sigma, \tau \} = {\bf R}^3,$
• $C_1(K) = {\rm span}\{e \} = {\bf R},$
• $C_0(K) = {\rm span}\{A \} = {\bf R}.$

The boundary operator: $$\partial \colon 0 \rightarrow {\bf R}^3 \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow 0.$$

• $\dim 0$:

$$Z_0(K) = C_0(K).$$

Always, since $\partial \colon {\bf R} \rightarrow 0$, its kernel is the whole domain. So $$Z_0(K) = {\rm span}\{A \}.$$

Next, $$\partial e = A - A = 0,$$ so $$B_0(K) = {\rm span}\{∂e \} = 0,$$ so $$H_0(K) = Z_0(K) / B_0(K) = {\rm span}\{A \} / 0 = {\rm span}\{A \}.$$

So, there is only one piece here.

• $\dim 1$:

Since $\partial e = 0$, the boundary operator $$\partial \colon C_1(K) = {\rm span}\{e \} \rightarrow C_0(K) = {\rm span}\{A \}$$ is zero.

Hence, $$Z_1(K) = {\rm ker \hspace{3pt}} \partial = {\rm span}\{e \}.$$

Observe: $$\begin{array}{l} \partial \mu = -e, \\ \partial \sigma = e, \\ \partial \tau = e. \end{array}$$

Then $$B_1(K) = {\rm span}\{ \partial \mu, \partial \sigma, \partial \tau \} = {\rm span}\{e \},$$ and $$H_1(K) = Z_1(K) / B_1(K) = {\rm span}\{e \} / {\rm span}\{e \} = 0.$$

So, there are no non-trivial loops here.

• $\dim 2$:

Since the dimension of the image of the boundary operator $$\partial \colon C_2(K) = {\rm span}\{ \partial \mu, \partial \sigma, \partial \tau \} \rightarrow C_1(K) = {\rm span}\{e \}$$ is $1$, then the dimension of its kernel is $3 - 1 = 2$.

Let's find its basis by solving the system of linear equations $\partial x = 0$. By examination: $$\partial (\mu + \tau) = e - e = 0,$$ $$\partial (\mu + \sigma) = e - e = 0,$$ so $\{\mu + \tau, \mu + \sigma \}$ is a basis of $Z_2(K)$. Finally, $$H_2(K) = Z_2(K) / B_2(K) = {\rm span}\{\mu + \tau,\mu + \sigma \} / 0 = {\rm span}\{ \mu + \tau,\mu + \sigma \}.$$

These two elements represent the two voids in the sphere. (Note: $\mu - \tau, \sigma + \mu$, etc may also form a basis.)

Exercise. Compute the homology of the sphere with a string from $N$ to $S$.