This site is being phased out.
Homology and algebra
Redirect to:
Oriented vs non-oriented chains
The homology of a cubical complex was introduced as a collection of homology classes. By its nature this was a combinatorial approach as there was no algebraic relation between the homology classes. The problem with this approach is that it does not allow us to derive the topological characteristics of the complexes, such as Betti numbers from the homology. Two relevant examples are below.
Suppose complex $3{\bf P}$ consists of $3$ distinct $0$-cells, only: $A, B, C$. Then $A, B$, and $C$ are cycles and they are non-homologous. But so are $A+B$, $B+C$, $C+A$, $A+B+C$. All of them generate distinct, non-zero homology classes. The total number is $7$. Then where does the Betti number come from? $$B_0(3{\bf P}) = 3.$$
There are $3$ components after all. The answer is: there are $3$ generators of this group: $$H_0(3{\bf P}) = <[A], [B], [C]>.$$
In the above representation, this group is (we have to include $0$) $$H_0(3{\bf P}) = {\bf Z}_2 \times {\bf Z}_2 \times {\bf Z}_2.$$
A slightly more complex example is given by the figure eight ${\bf F}8$:
- $0$-cells: $A, B, C, D, E, F$
- $1$-cells: $a, b, c, d, e, f, g$
- Boundary operator: $\partial a = A + B$, $\partial b = B + C$, etc
We "know" what the answer should be: $$B_1({\bf F}8) = 2.$$
Two holes! But there are many non-homologous cycles: $$\begin{array}{l} x = a + b + c + d, \\ y = c + e + f + g, \\ z = a + b + e + f + g + d. \end{array}$$
(Others would be reduced to these by the cancellation $2u=0$.) Fortunately, $$z = x + y.$$
So this group has two generators. In fact,
$$H_1({\bf F}8) = {\bf Z}_2 \times {\bf Z}_2.$$
Thus the $k$-th Betti number of complex $K$ is simply the number of generators in the $k$-th homology group. The latter is known as the rank of the group. Thus, $$B_k(K) = {\rm rank}( H_k(K) ).$$
The above approach is referred to as homology over ${\bf Z}_2$. Indeed the "cancellation rule" $2u=0$ means that all non-zero elements have order $2$.
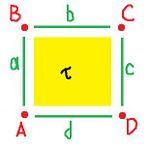
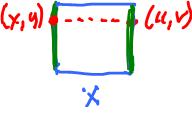
In the second example, let's consider how we build the cylinder from the square. The complex $K$ of the square is:
- $0$-cells: $A, B, C, D$
- $1$-cells: $a, b, c, d$
- $2$-cells: $\tau$
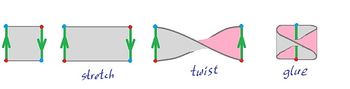
We can create the cylinder ${\bf C}$ by gluing two opposite edges. We can also interpret the gluing as equivalence of $a$ and $c$: $$a \sim c.$$
Suppose now that we want to build the Mobius band ${\bf M}$ from the square. Once again we can interpret the gluing as equivalence of $a$ and $c$. But this time they are attached to each other with $c$ upside down. It makes sense then to interpret this as this equivalence: $$a \sim -c.$$
This suggests that we can use the "negative" of a cell when forming chains. Then the chain complex will include all (integer) linear combinations of the cells, such as for example:
$$z = 2a - b + 3e - 17g + d.$$
This will make the chain complexes and the homology "larger" that will still have the same number of generators. In the above examples: $$\begin{array}{l} H_0(3{\bf P}) = {\bf Z} \times {\bf Z} \times {\bf Z}, \\ H_1({\bf F}8) = {\bf Z} \times {\bf Z}. \end{array}$$
If you allow the real coefficients in the chains, the results are:
$$\begin{array}{l} H_0(3{\bf P}) = {\bf R} \times {\bf R} \times {\bf R}, \\ H_1({\bf F}8) = {\bf R} \times {\bf R}. \end{array}$$
The latter groups are in fact vector spaces. These are respectively homology over ${\bf Z}$ (or integer homology) and homology over ${\bf R}$. The choice among these three (and others: ${\bf Z}_p$, ${\bf C}$, ${\bf Q}$, etc) might make a difference in capturing more subtle homological features of the complex. The difference lies in the torsion of these groups. The Betti numbers will be the same though.
As it turns out, the negative of a cell is the same cell with the "opposite orientation", i.e., the order of vertices.
The boundary operator and homology
Again, chains over the reals give us vector spaces of chains.
Among all the chains, we are interested firstly in the ones that capture topological features: components, tunnels, voids etc.
Consider tunnels (holes in 2D). As we saw previously, tunnels are captured by closed curves. Such a curve can certainly be made of just the edges ($1$-cells) followed consecutively until you come back to the first vertex. What is so special about such a collection of edges? Every edge has another one attached to its end points by its initial point. Therefore each vertex appears twice. If the curve revisits the vertex one more time, then the vertex appears four times, etc. Thus each vertex appears, as an end point of an edge, an even number of times. Therefore the boundary of this chain is $0$.
So, the algebraic analogue of a closed curve is a chain with $0$ boundary.
Definition. A chain $C$ is called a cycle if $$∂C = 0.$$
If $C$ is a $k$-chain, we call it $k$-cycle.
Since the boundary of any $0$-cell is $0$, all $0$-chains are cycles. As we just showed, $1$-cycles correspond to closed (parametric) curves. A similar argument will show that $2$-cycles correspond to closed (parametric) surfaces.
Since there are many chains that capture the same topological feature, we combine them into equivalence classes. The way it was done previously:
- two points are homologous if they are the end points of a curve.
- two closed curves are homologous if they form a boundary of a surface.
- two closed surfaces are homologous if the are the boundary of a solid.
This time everything is entirely algebraic.
Definition. Two $k$-cycles $A$ and $B$ are homologous $(A \sim B)$ if they are the boundary of a $(k+1)$-chain: $$∂C = A + B.$$
Example.
Dimension 0: Two $0$-cycles are homologous if there is a path between them made of edges.
Dimension 1: Two $1$-cycles are homologous if there is a chain connecting them made of faces.
Dimension 2: Exercise...
Exercise. Prove that for a $1$-chain $a$, $\partial a=0$ iff $a$ is a closed curve (i.e., $1$-cycle). Solution: 
Exercise. Show that homology is an equivalence relation.
Now, each homology class captures a single topological feature of the complex in each dimension.
Definition. The $k$-th homology $H_k(K)$ of complex $K$ is the set of all $k$-homology classes of $K$.
We can also write $$H_k(K) = H_k(|K|) = H_k(X).$$
The homology class of the trivial chain $0$ is denoted by $0$. We include it in $H_k(K)$. It is a matter of convenience for now but in the future this becomes crucial as we treat the homology as a group.
Exercise. Show that for any $0$-chain $A$, $A \sim 0$ if and only if $A = 0$.
Exercise. Compute the homology of the complex. Solution: 
Exercise. Prove that for any cubical complex $K$, $H_0(K)$ has only one non-zero element if and only if its realization $|K|$ is (path) connected. (Note that in the case of path connectedness, the points being connected don't have to be vertices and the path doesn't have to be made of edges. Illustration: 
) Hint: Think of edges as streets, vertices as intersections, cells as parking lots, $0$-homology as a turn-by-turn instructions from an intersection to another. Solution: 
Theorem. Homology is a topological invariant.
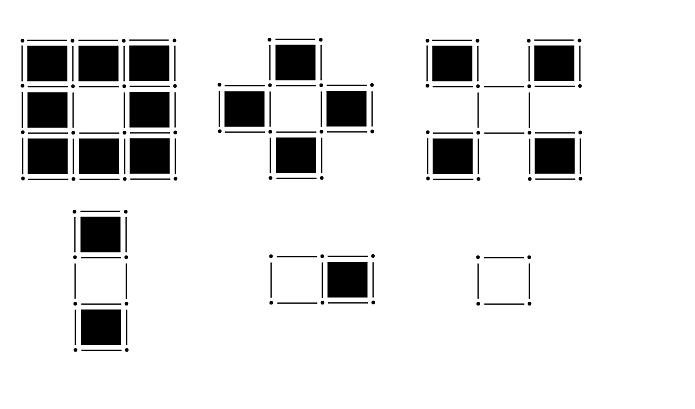
To illustrate, the homology of the six complexes below is the same, that of the circle.
Proving theorems like this requires some build-up...
When is the homology trivial?
When every cycle is a boundary!
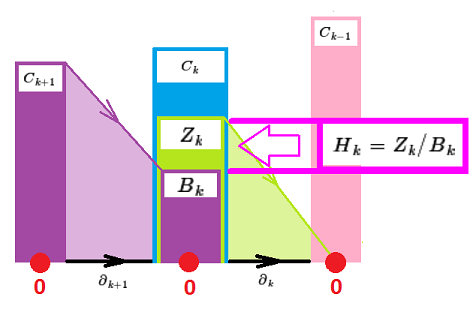
It is illustrated by this familiar diagram:
