This site is being phased out.
From continuity to point-set topology
Redirect to:
Our interest is mainly is algebraic topology. Consequently, point-set topology will be limited to that of the euclidean space, "nice" subsets of the euclidean space, such as cells, and "nice" combinations of those.
Since algebra will take care of how these pieces fit together globally to form components, holes, voids, etc, here, in a way, we are interested in local topological properties.
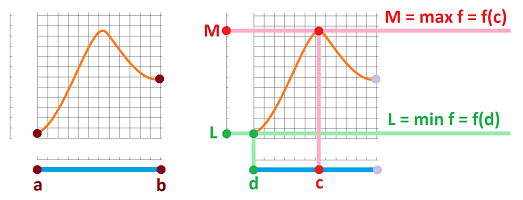
Let's recall one topological theorem from calculus. Under appropriate circumstances, a function $f$ may have attain its extreme values:
In fact, we have
Extreme Value Theorem. If $f$ is continuous on $[a,b]$, then there is $c,d$ in $[a,b]$ such that $f(c) = M,f(d) = L$, where $M,L$ are the maximum and minimum values of $f$ on $[a,b]$ respectively.
So, let's take a look at continuity.
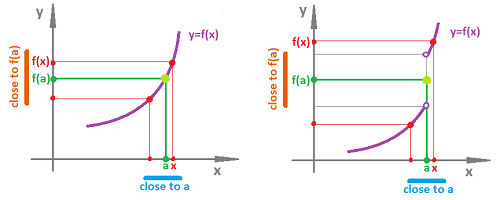
Recall from calc 1, that continuity of function $f \colon {\bf R} \rightarrow {\bf R}$ at point $x=a$ can be introduced in terms of closeness (proximity):
That's on the left. On the right, even though $x$ is close to $a$, $f(x)$ does not have to be close to $f(a)$: the discontinuity of the function does not allow us to control its output.
This is the usual definition of continuity of $f$ at point $x=a$:
The second part can be restated as:
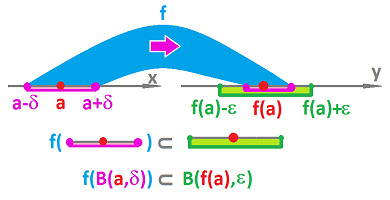
This says simply that $f$ takes a certain set on the $x$-axis to another set on the $y$-axis: $$f\left( (a-\delta,a+\delta) \right) \subset \left( f(a)-\epsilon, f(a)+\epsilon \right).$$ These sets are open intervals but can be also seen as "balls": $$f\left( B(a,\delta) \right) \subset B \left( f(a), \epsilon \right),$$ where $B(p,d)=\{u \colon |u-p| < d \}$.
In calculus we see a lot of examples of functions between higher-dimensional Euclidean spaces $f:{\bf R}^n \rightarrow {\bf R}^m$: parametric curves, parametric surfaces, vector fields, etc. To accommodate this need we re-write the last part of the definition with the norm replacing the absolute value: $$||x - a|| < \delta \Rightarrow || f(x) - f(a) || < \epsilon.$$
This isn't general enough as we want to deal with any subsets of the Euclidean space. Therefore we need to adjust the definition a bit more.
Definition. A function $f:X \rightarrow Y$ with $X \subset {\bf R}^n, Y \subset {\bf R}^m$ is called continuous at $x=a \in X$ if for any $\epsilon > 0$ there is a $\delta > 0$ such that $$||x - a|| < \delta,x \in X \Rightarrow || f(x) - f(a) || < \epsilon.$$
Observe that with this definition we don't have to deal with "continuity from the left/right" anymore.
Definition. $f$ is called continuous if it is continuous at every point of its domain.
Note: "Discuss continuity of $1/x$" will be answered in a very different way now. Compare:
- Calc 1: $1/x$ is discontinuous at $x=0$ (... and continuous on $(-\infty,0)\cup (0,\infty)$).
- Topology: Function $f:(-\infty,0)\cup (0,\infty) \to {\bf R}$ given by $f(x)=1/x$ is continuous.
...because we don't even consider continuity at a point where the function is undefined (consider extensions of functions though).
As before, the inequalities indicate simply that $f$ takes $x$ in a certain set in the domain of $f$ to $y=f(x)$ in another set in its range:
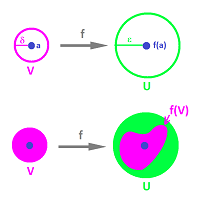
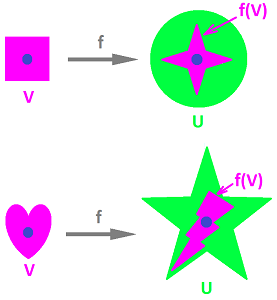
where $B(p,d)= \{u \colon ||u-p|| < d \}$. This can be re-written as $$f \left( B(a, \delta) \right) \subset B \left( f(a) , \epsilon \right).$$ To put it simply, $$f( V ) \subset U,$$ where $$V=B(a, \delta), U=B \left( f(a) , \epsilon \right).$$ So, in dimension $2$, the relation between these sets is illustrated as follows:
Suppose now that
- $\gamma _X$ is the set of all open balls in $X={\bf R}^n$, and
- $\gamma _Y$ is the set of all open balls in $Y={\bf R}^m$.
We can restate the definition in a more abstract -- and more compact! -- form:
Another advantage of this approach is seen in our ability to handle subsets in the same manner as the whole Euclidean space:
We just choose for $\gamma _X$, instead of balls, intersections of the balls with $X\subset {\bf R}^n$: $$\gamma _X = \{ B(x,\delta)\cap X: x\in X,\delta>0 \}.$$
Further, these balls can be easily replaced with sets of any other shape:
The importance of these intervals, disks, and balls is the reason why we start studying topology by studying these collections of sets. We will call them neighborhoods. For example, $B(a, \delta)$ is a "ball" neighborhood of $a$.
The difference now is that, since we only discuss continuity one point at a time, we don't need a single yardstick to measure distances everywhere. We just need the ability, for each $a \in X$, to answer the question: "How close is $x$ to $a$?" And the answer doesn't look that different:
- Calc 1: "It's within $\delta$";
- Topology: "It's within $V$".
However, all references to numbers are gone!
In order to have a meaningful concept of continuity we need these sets of neighborhoods to satisfy certain properties...
First, we want to be able to discuss continuity of $f:X\to Y$ at every point $a\in X$. So, these neighborhoods have to cover the whole set:
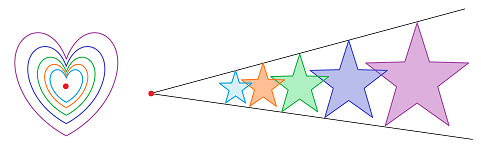
That's not all. We also want to be able to zoom in on every point -- to detect breaks. So, the collection $\gamma$ should be "refinable":
This is how we understand the refining process, illustrated with disks:
To summarize:
- (B1) $\cup \gamma = X$.
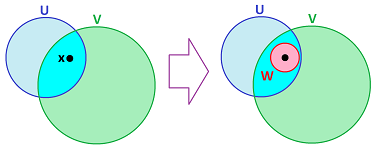
- (B2) For any neighborhoods $U, V\in \gamma$ and any point $c\in U\cap V$ in their intersection, there is a neighborhood $W\in \gamma$ of $c$ such that $W \subset U \cap V$.
So, as it turns out, this is all the extra structure we need to be able to study continuity on a set.
Definition. Suppose $X$ is any set. Any collection $\gamma$ satisfying properties (B1) and (B2) is called a basis of neighborhoods in $X$.
And the new definition is wonderfully compact:
Definition. Given two sets $X,Y$ with bases of neighborhoods $\gamma_X,\gamma_Y$, function $f:X\to Y$ is continuous if for any $U \in \gamma _Y$ there is $V \in \gamma _X$ such that $f( V ) \subset U$.