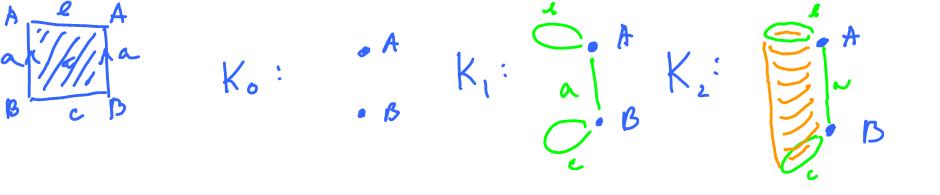Examples of cell complexes

Redirect to:

• Cell complex

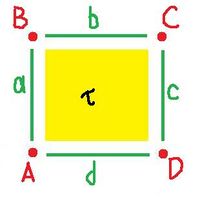
Let's see what we can build from the square:

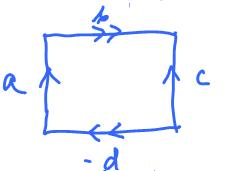
The complex $K$ of the square is:

• $0$-cells: $A, B, C, D$;
• $1$-cells: $a, b, c, d$;
• $2$-cells: ${\tau}$;
• boundary operator: ${\partial}{\tau} = a + b + c + d; {\partial}a = A + B, {\partial}b = B + C$, etc.

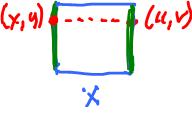
Now, we can create the cylinder $C$ by gluing two opposite edges with the following equivalence relation: $$(0,y) \sim (1,y).$$

The cells of the cell complex are identified too:

• $a \sim c;$
• $A \sim D, B \sim C.$

We sill have our collection of cells (with some identified) only the boundary operator is different:

• ${\partial}{\tau} = a + b + c + d = a + b + a + d = b + d;$
• ${\partial}a = A + B, {\partial}b = B + C = 0, {\partial}c = A + B, {\partial}d = D + A = 0.$

In order to build the Mobius band ${\bf M}^2$ the equivalence relation is $$(0,y) \sim (1,1-y).$$

And the equivalence of cells is:

• $a \sim -c.$

Here $-c$ represents edge $c$ with the opposite orientation. Further

• $A \sim D, B \sim C.$

The boundary operator is:

• ${\partial}{\tau} = a + b + c + d = a + b - a + d = b + d;$
• ${\partial}a = A + B, {\partial}b = B + C = 0, {\partial}c = A + B, {\partial}d = D + A = 0.$

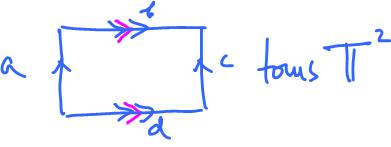
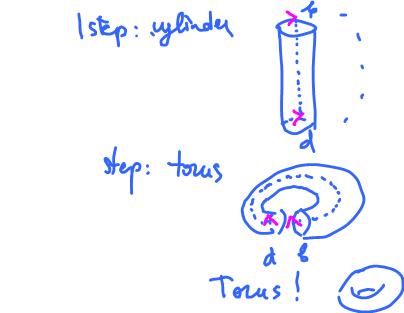
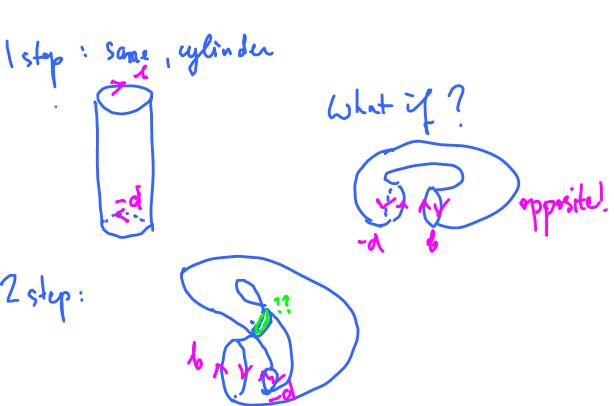
What if after creating the cylinder by identifying $a$ and $c$ we also identify $b$ and $d$? The result is the torus ${\bf T}^2$.

The diagram of the identification is on the right and below is the actual gluing construction.

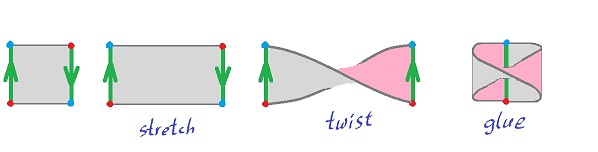
Example. What if we flip one of the edges? Like this:

• $a \sim c,$
• $b \sim -d.$

The result is called the Klein bottle. If we try to follow the gluing procedure we used for the cylinder, we get stuck because $b$ and $-d$ aren't aligned and can't be glued together. We have to flip $d$ for alignment but then to get the ends of the cylinder together we have to go through its side!

Fortunately, it can be done via $4$th dimension. Besides, the gluing diagram is the Klein bottle (defined as a quotient space).

Exercise. What if we flip both? Like this:

• $a \sim -c,$
• $b \sim -d.$

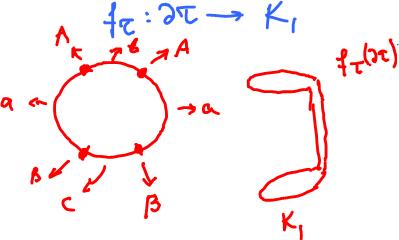
Example. Let's explore more thoroughly the cell complex structure of the cylinder by explicitly presenting both the skeleta and the gluing maps.

The formulas for the gluing maps for the 1-skeleton are simple. Suppose,

• $a = b = c = [0,1]$,

then

• $f_a(0) = A, f_a(1) = B;$
• $f_b(0) = f_b(1) = A;$
• $f_c(0) = f_c(1) = B.$

For the $2$-skeleton, we'll use a diagram to present the only gluing map $f_{\tau}$. Since ${\tau}$ is a disk, we only need to show where in $K_1$ the points on its boundary ${\bf S}^1$ are taken. Below we show the preimages of the cells in $K_1$:

• the preimages of the $0$-cells $A, B$ are $2$ points for each,
• the preimages of the three $1$-cells $a, b, c$ are one arc, two arcs, one arc, respectively.

Exercise. Find other ways to attach the $2$-cells to the $1$-skeleton. Solution:

Exercise. Following the procedure above represent the following surfaces as cell complexes:

• the Mobius band,
• the torus,
• the Klein bottle,
• the projective plane.

Example. A simple example of a higher dimensional cell complex is the $n$-sphere. It is made of two cells:

• $0$-cell $A$ and $n$-cell ${\tau}$.

The skeleta are:

• $K_0 = ... = K_{n-1} = \{A \}.$

The gluing map is constant:

• $f_{\tau}(x) = A.$

Hence:

• $K_n = {\bf S}^n.$

Exercise. Represent the sphere as a cell complex with two $2$-cells, list all cells, and describe/sketch the gluing maps. Solution: