Boundary operator of simplicial complexes

Redirect to:

• Simplicial homology

The boundary operator is much easier to handle if you choose to use simplicial complexes.

We need to prove the key fact needed for homology theory:

boundaries have no boundaries

or, algebraically, $$\partial \partial( \tau ) = 0$$ for any chain $\tau$.

Recall that a collection $K$ of subsets of set $S$ is called an abstract simplicial complex if all subsets of any element of $K$ are also elements of $K$, i.e.,

if $\tau \in K$ and $\sigma < \tau$ then $\sigma \in K$.

In this sense, what is an abstract $n$-simplex? It's simply any finite set $$s = A_0A_1...A_n.$$

It suffices to prove that $\partial \partial (s) = 0$ for any simplex $s$ in $K$.

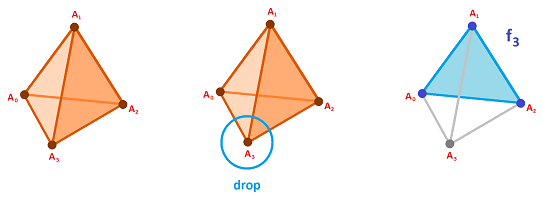
Recall first what are the faces of a simplex.

As the $n$-simplex is just a list of $n+1$ vertices, any of its $(n-1)$-faces is a list of the same vertices with one dropped (indicated by parentheses):

$$f_0 = [A_0]A_1...A_n,$$ $$f_1 = A_0[A_1]...A_n,$$ $$...$$ $$f_n = A_0A_1...[A_n].$$

The $(n-2)$-faces will miss two vertices: $$f_{ij} = A_0...[A_i]...[A_j]...A_n, $$

Now the boundary of $s$ is the alternating sum of its faces:

$\partial s = f_0 - f_1 + f_2 - ... \pm f_n$, or

$$\partial s = \sum_i (-1)^i A_0A_1...(A_i)...A_n.$$

Theorem. $\partial \partial = 0$.

Proof. The idea is that in $\partial \partial s$ each $(n-2)$-face appear twice but with the opposite sign.

We use the definition and then linearity of the boundary operator: $$\begin{array}{} \partial \partial s &= \partial( \sum_i (-1)^i A_0A_1...[A_i]...A_n ) \\ &= \sum_i (-1)^i \partial(A_0 A_1...[A_i]...A_n) \end{array}$$ Consider each term: $$\begin{array}{} \partial(A_0 A_1...[A_i]...A_n) \\ &= \sum_{j<i} (-1)^{j-1} [ A_0A_1...[A_i]...[A_j]...A_n \text{ ($A_j$ in position } (j-1)) \\ & + \sum_{i < j} (-1)^j A_0 A_1 ... [A_j] ... [A_i]... A_n . \end{array}$$ Therefore $$\begin{array}{} \partial \partial s & = \sum_{i < j} (-1)^{i+j-1} A_0 A_1...[A_i]...[A_j]...A_n + \sum_{i > j} (-1)^{i+j} A_0 A_1...[A_j]...[A_i]...A_n. \end{array}$$

These terms are put in a $(n-1) \times (n-1)$ table with the first part above the diagonal, the second part below, the diagonal empty. The entries in the table symmetric with respect to the diagonal have the same face, $f_{ij}$, but with opposite signs. So, they all cancel. $\blacksquare$

So, the boundary of the boundary of a cell is zero. Since every chain is a linear combination of cells, it follows from the linearity of ${\partial}$ that the boundary of the boundary of any chain is zero: $$C_k(K) \xrightarrow{\partial} C_{k-1}(K) \xrightarrow{\partial} C_{k-2}(K)$$ $${\tau} \mapsto 0.$$

In other words, the square of the boundary operator is the zero operator: $${\partial}{\partial} = 0.$$

The cap product is a bilinear map on homology and cohomology: $$\frown : H_p(X)\times H^q(X) \rightarrow H_{p-q}(X),$$ defined by multiplying a $p$-chain $\sigma$ in $X$ by a $q$-cochain $\psi$ in $X$ evaluated on $(p-q)$-faces of the simplices of $\sigma$. It is defined using the linearity by starting with simplices. So, given a simplex $\sigma =A_0 A_1... A_q...A_n$ and a cochain $\psi$, then: $$\sigma \frown \psi = A_0 A_1 ... A_q ... A_n \frown \psi = \psi(A_0 A_1 ... A_q) \cdot A_q ... A_n .$$

The boundary operator and coboundary operator on chain/cochains behaves like this: $$\partial(\sigma \frown \psi) = (-1)^q(\partial \sigma \frown \psi - \sigma \frown \delta \psi). $$ In addition, given a map $f$, the induced homology and cohomology operators satisfy: $$f_*( \sigma ) \frown \psi = f_*(\sigma \frown f^* (\psi)).$$