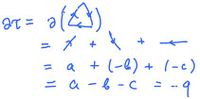Boundary operator

Redirect to:

• Chain complex

Recall that given a cell complex $K$, a $k$-chain is a "formal" linear combination of finitely many oriented $k$-cells, such as $3a + 5b - 17c$ with, typically, integer coefficients.

The set of all $k$-chains $C_k(K)$ is called the chain complex: $$C_k(K) = \left\{ \displaystyle\sum_i s_i \sigma_i \colon s_i \in {\bf Z}, \sigma_i {\rm \hspace{3pt} is \hspace{3pt} a \hspace{3pt}} k{\rm -cell \hspace{3pt} in \hspace{3pt}} K \right\}$$

The boundary operator captures a relation between cells/chains of different dimensions in order to capture the topology of the cell complex.

The boundary of a vertex empty, so the boundary operator of a $0$-chain is $0$: $$\partial (A) = 0 {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} A \in C_0(K).$$

The boundary of a $1$-cell consists of its two end-points, so in the binary setting this was simple: $$\partial (a) = \partial (AB) = A + B.$$

In the integral setting, the direction of the edge matters ($AB \neq BA$), so we define: $$\partial (a) = \partial (AB) = B - A {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} a = AB \in C_1(K).$$

With the operator defined on each of the cells, one can extend this definition to the whole chain complex, by assuming that $\partial$ is a homomorphism (or a linear operator in the vector space case):

if $a = \displaystyle\sum_i s_i \sigma_i, s_i \in {\bf Z}$, then $\partial(a) = \displaystyle\sum_i s_i \partial( \sigma_i )$.

Example:

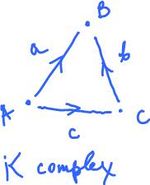
In dimension $2$, suppose we have a cell complex $K$:

• $0$-cells: $A, B$,
• $1$-cells: $a = AB, b = CB, c = AC$,
• $2$-cells: $\tau = ABC$.

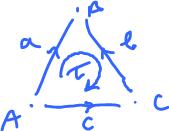
The the boundary $\partial \tau$ is defined as a linear combination of its faces: $$\partial \tau = AB + BC + CA = a + b - c,$$

or:

Here we first follow the chain around clockwise as indicated by its orientation writing the $1$-cells as they appear, and then interpret these $1$-cells in terms of the $1$-cells, $a, b, c$, that we recorded in the cell complex $L$. It can be extended to the whole chain complex $C_2(L)$.

Example:

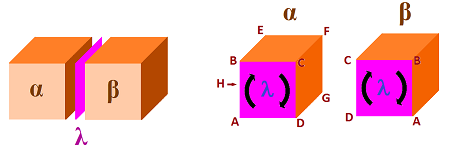
In dimension $3$, there is only one $$3{\rm -cell} \colon \alpha = ABCDEFG$$ with the orientation given by this particular order of vertices. Next, $$2{\rm -cells} \colon \tau = ABCD, \sigma = BCFG, \lambda = CFED,$$ with the orientations indicated by the arrows just as in the above example. To compute the boundary of $\alpha$ we need to express its faces in terms of these $2$-cells, plus or minus. These faces are obtained by dropping one of the vertices from the list $ABCDEFG$: $$\begin{array}{l} \partial \alpha &= ABCD + BCFG + CDEF + 3 {\rm \hspace{3pt} more} \\ &= \tau + \sigma - \lambda + 3 {\rm \hspace{3pt} more}. \end{array}$$

Why the minus sign? Let's see how many transpositions it takes to turn $\lambda = CFED$ into $CDEF$. $$CFED \rightarrow CEFD \rightarrow CEDF \rightarrow CDEF.$$

Three. Since it's odd, $CDEF = - CFED = -λ$.

More generally, the boundary of a $k$-cell is a collection of $(k-1)$-cells, i.e., a $(k-1)$-chain. Since we are dealing with groups, we want it to be a homomorphism: $$\partial \colon C_k(K) \rightarrow C_{k-1}(K).$$

And, if we know $\partial (\sigma_i)$ for each cell $\sigma_i \in C_k(K)$, we can simply extend $\partial$ to the rest of the group: $$\partial \left( \displaystyle\sum_i s_i \sigma_i \right) = \displaystyle\sum_i s_i \partial( \sigma_i ).$$

The key fact needed for homology theory is:

boundaries have no boundaries

or, algebraically, $$\partial \partial = 0.$$

In other words,

for any $x \in C_k(K), \partial(\partial(x)) = 0 \in C_{k-2}(K)$.

For $k<2$, the fact is obvious. For $k=2$, it is easy to prove.

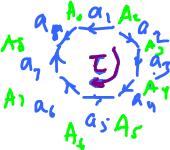
Example: Let's do that for this $2$-cell, with the orientations of $1$-cells randomly assigned.

Then $$\partial \tau = -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8,$$

$$\begin{array}{l} \partial (\partial \tau) &= \partial( -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8 ) \\ &= -\partial a_1 + \partial a_2 + \partial a_3 + \partial a_4 - \partial a_5 + \partial a_6 + \partial a_7 - \partial a_8 \\ &= -(A_1 - A_2) + (A_3 - A_2) + (A_4 - A_3) + (A_5 - A_4) \\ & - (A_5 - A_6) + (A_7 - A_6) + (A_8 - A_7) - (A_8 - A_1) \\ &= 0. \end{array}$$

The pattern in clear.

It's not as easy in higher dimensions. We will switch to simplicial complexes to tackle that - see Boundary operator of simplicial complexes.

Thus every boundary is a cycle:

$B_k$ $\subset$ $Z_k$.

That's why homology group makes sense: $$H_k = B_k / Z_k.$$