This site is being phased out.
Algebra of differential forms
Redirect to:
Here we will devise a set of algebraic axioms that rule differential forms.
Contents
Algebraic properties of forms
For now, $1$-forms in the $3$-space appear to be functions of $x$, $y$, $z$, $dx$, $dy$, and $dz$ that are linear on $dx$, $dy$, and $dz$ (those are called differentials in calculus).
For example, we see below that $\phi = x^2 dx + xy dy$ is a linear function of $dx$ and $dy$, non-linear for $x,y$.
- Suppose we have two pairs of differentials: $dx,dy$ and $dx',dy'$ (meaning another value of the same variable). Consider replacing $dx$ and $dy$ in $\phi$ by $dx + dx'$ and $dy + dy'$. In this case we get
$$x^2 (dx + dx') + xy(dy + dy') = (x^2 dx + xy dy) + (x^2 dx' + xy dy').$$ This is called additivity.
- Let $\alpha \in {\bf R}$ and consider replacing $dx$ with $\alpha dx$ and $dy$ with $\alpha dy$ in $\phi$. In this case we get
$$x^2(\alpha dx) + xy(\alpha dy) = \alpha x^2 dx + \alpha xy dy = \alpha(x^2 dx + xy dy).$$ This is called homogeneity.
So $1$-forms are linear on the second argument. What about $2$-forms?
They are not quite as simple.
Consider the $2$-form $\varphi = xy dx \hspace{1pt} dy$, and let's try to verify that it is linear.
- If we try to verify additivity, and we compute $xy (dx + dx')(dy + dy')$, we get a mess.
- If we try to verify homogeneity, and we compute $xy (\alpha dx)(\alpha dy) = \alpha^2 xy dx \hspace{1pt} dy$, we have no match!
Conclusion: they aren't linear!
OK, in what sense are $2$-forms linear?
They are
- linear on $dx$,
- linear on $dy$,
- not linear on $(dx,dy)$!
Also, keep in mind that here $dx,dy$ aren't numbers but forms!
We easily verify that it is indeed linear on $dx$:
- We verify additivity in $dx$ by computing $xy (dx + dx')dy = xy dxdy + xy dx'dy$.
- We verify homogeneity in $dx$ by computing $xy (\alpha dx)dy = \alpha xy dx \hspace{1pt} dy$.
To summarize, we see that differential forms are multilinear, i.e., linear with respect to each variable as all others are fixed.
What about symmetry? That is, is it similar to the dot product: $$<x,y>=<y,x>?$$
It turns out that differential forms are not symmetric but anti-symmetric. That is, they are more like the cross product: $$x \times y = -y \times x.$$ In particular, for 2-forms, this results in the equivalence $$dx \hspace{1pt} dy = -dy \hspace{1pt} dx.$$
From this rule it follows, for example, $$dx \hspace{1pt} dy \hspace{1pt} dz = -dy \hspace{1pt} dx \hspace{1pt} dz = -(-dy \hspace{1pt} dz \hspace{1pt} dx) = dy \hspace{1pt} dz \hspace{1pt} dx.$$
We also have that $$dx \hspace{1pt} dx = -dx \hspace{1pt} dx$$ and therefore $$2dx \hspace{1pt} dx = 0$$ implying $$dx \hspace{1pt} dx=0.$$ This suggests the following.
Corollary: $dx \hspace{1pt} dx=0$, $dy \hspace{1pt} dy=0$, and $dz \hspace{1pt} dz=0$.
Where does this come from?
We think of differential forms as multilinear antisymmetric functions parametrized by location in ${\bf R}^n$: $$\varphi =\varphi ^k: {\bf R}^n \times ({\bf R}^n)^k \rightarrow {\bf R}.$$
The axiomatic definition of differential forms
Based on this insight we define forms as follows.
First, we are given the "ambient space" which will be assumed to be Euclidean, ${\bf R}^n$.
Second, the domain, or the location space, $R$ is given, which is a subset of the ambient space ${\bf R}^n$. Typically, it is an open subset.
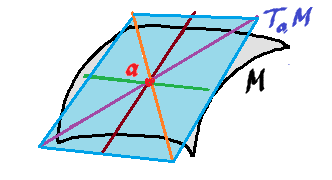
Below is a more advanced set-up, where $R=M$ an $n$-manifold and $V=TM$ is its tangent bundle:
Third, the tangent, or the direction space, $V$ is given, which is (isomorphic to) a subspace of ${\bf R}^n$. Typically, it is ${\bf R}^n$.
Finally, a continuous function $$\varphi =\varphi ^k: R \times V^k \rightarrow {\bf R}$$ is called a differential form of degree $k$ over $R$, or simply a $k$-form, if
- $\varphi$ is linear with respect to each $V$;
- $\varphi$ is antisymmetric with respect to $V^k$.
Note that neither $R$ nor $V$ inherit the geometric structure of ${\bf R}^n$. The former gets the topology and the latter gets the algebra. There is no geometry so far.
The set of such $k$-forms over $R$ is denoted by $\Omega ^k(R)$. It is a vector space.
The starting point of our analysis will be dimension $3$, where $k$-forms are these functions: $$\varphi =\varphi ^k : {\bf R}^3 \times ({\bf R}^3)^k \rightarrow {\bf R},$$ where
- the ${\bf R}^3$ part corresponds to the variables $x$, $y$, and $z$, and
- the $({\bf R}^3)^k$ part corresponds to $dx$, $dy$, and $dz$,
with the following properties with respect to each ${\bf R}^3$.
- Multilinearity:
- For $\varphi(\cdot,b,c)$ : $\varphi(\alpha u + \rho v,b,c) = \alpha \varphi(u,b,c) + \rho \varphi(v,b,c)$;
- For $\varphi(a,\cdot,c)$ : $\varphi(a,\alpha u + \rho v,c) = \alpha \varphi(a,u,c) + \rho \varphi(a,v,c)$
- For $\varphi(a,b,\cdot)$ : $\varphi(a,b,\alpha u + \rho v) = \alpha \varphi(a,b,u) + \rho \varphi(u,b,v)$
- Anti-symmetry:
- $\varphi(x,y,c) = -\varphi(y,x,c)$
- $\varphi(a,y,z) = -\varphi(a,z,y)$
- $\varphi(x,b,z) = -\varphi(z,b,x)$
We will show that this definition is satisfied by the forms introduced in the traditional way. However, note that the "traditional way" we started with doesn't provide a definition of forms, other than as expressions that serve as "integrands".
An alternative way of defining forms as functions is as continuous maps $$\varphi = \varphi ^k: R \rightarrow \Omega^k (point) =\Lambda ^k.$$ It is based on the following well-known exponential identity of functions: $$[X \times Y,Z]=[X,[Y,Z]],$$ where $[A,B]$ stands for the set of functions from $A$ to $B$. The bijection is seen via: $$f(x,y)=f(x)(y).$$
The vector space of differential forms
Let's consider the set $\Omega^k$ of all $k$-forms. The algebra that we have considered gives it an extra structure.
It is a vector space under the usual addition and scalar multiplication of functions: $$+ \colon \Omega^k \times \Omega^k \rightarrow \Omega^k,$$ $$\cdot \colon {\bf R} \times \Omega^k \rightarrow \Omega^k.$$ The only thing to be verified is the fact that the multilinearity and the antisymmetry are preserved under these operations (Exercise).
What is the dimension of this vector space?
One can start with degree $k=0$. Then $\Omega ^0$ is simply the space of all continuous functions. Its dimension is infinite. To prove that just consider all polynomials (Exercise).
For higher dimensions, $\Omega ^k$ contains these functions as well and, therefore, is infinite-dimensional as well.
But what if we limit ourselves to a fixed location? In this case, $1$-forms are just functions $\varphi ^1(a,\cdot)$. They are linear functions defined on a finite-dimensional space. The space they form is then finite-dimensional. One can think of this space as simply $\Omega ^k(p)$, where $p$ is a point in ${\bf R}^3$.
Let's compute the dimensions of these spaces.
The $k$-forms are linear functions $$\varphi ^k: ({\bf R}^n)^k \rightarrow {\bf R}.$$ Since the dimension of the domain space is $nk$ and that of the target space is $1$, these are represented by matrices $1 \times nk$. Therefore, the dimension of this space is $nk$.
Let's compare this result to the original definition of $k$-forms. For example, $2$-forms in $3$-space look like this: $$Adxdy+Bdydz+Cdzdx.$$ Since the (numerical) coefficients $A,B,C$ vary independently, the dimension of this space is $3$. But it's $6$ according to the above formula.
Exercise. Find out what is wrong here and provide the correct solution.
Back to $1$-forms as combinations $dx,dy$
From the axiomatic definition we now circle back to the traditional one, i.e., differential forms as "combinations" of $dx,dy,dz$.
How do we make sense of them?
It all starts when the domain $R={\bf R}^n$ is supplied with a coordinate system. Suppose $\{e_1,...,e_n\}$ is a basis. It is important to remember that this is an ordered basis, i.e., interchanging any two element amounts to a new basis that require change of variables etc. This assumption makes the space "oriented". This assumption explains why $dxdy \ne dydx$.
In that case, all points of $R$ are expressed in terms of their coordinates with respect to this system: $$x \in R \Rightarrow x=(x_1,...,x_n).$$ This means that these are the location variables of our form $\varphi ^k$: $$x_1,...,x_n.$$
What about the direction variables?
It is tempting to call them $dx_1,...,dx_n$ and that's they way it is frequently done. However, as we have seen, $dx,dy$, etc are $1$-forms! Then, in our axiomatic definition, we would have $dx$ that has $dx$ as a variable...
We choose these names: $$v \in V \Rightarrow v=<v_1,...,v_n>.$$ Here "$v$" stands for "velocity". Then our direction variables are: $$v_1,...,v_n,$$
However, this is enough only for $1$-forms and for higher degree forms we need more of those. These are the variables of a $k$-form in $n$-space: $$v^1_1,...,v^1_n;$$ $$v^2_1,...,v^2_n;$$ $$...$$ $$v^k_1,...,v^k_n.$$ Notice that the coordinate free representation is much simpler: $$\varphi(a,v^1,...,v^k),$$ where $a \in R,v^i \in V$. However, our interest right now is to learn how to express forms in terms of a specific coordinate system.
As these lists of variables are quite cumbersome, we'll stay in lower dimensions and use
- for location variables: $x,y,z$;
- for direction variables: $v_x,v_y,v_z$, and possibly $v'_x,v'_y,v'_z$ etc.
What are the $0$-forms? They are just functions.
What about $1$-forms?
To approach this, we start by trying to understand the meaning, in the sense of the axiomatic definition, of $dx$ and $dy$ in ${\bf R}^2$.
Just as for all forms, we have $$dx:{\bf R}^2 \times {\bf R}^2 \rightarrow {\bf R}.$$ Let's make it the simplest one of all, besides the zero. Just look at the input variables: $$dx(x,y,v_x,v_y)=?$$ It can't be a non-zero constant, because of the required linearity, so we put $$dx(x,y,v_x,v_y)=v_x,$$ and then $$dy(x,y,v_x,v_y)=v_y.$$ What makes these especially simple is that their values are independent of location.
Now, what about the rest of $1$-forms?
We know that they are to be found all as $$\varphi^1=Adx+Bdy,$$ where $A=A(x,y),B=b(x,y)$ are just (continuous) functions. This representation still makes sense in light of our new understanding of the two basic forms. Indeed, we just evaluate this formula with the usual meanings of the algebraic operations: $$\varphi^1(x,y,v_x,v_y)=A(x,y) \cdot v_x+B(x,y) \cdot v_y.$$
The only question remains: does this function satisfy the axiomatic definition?
For $1$-forms we just need to verify linearity with respect to $(v_x,v_y)$. An easy exercise.
It is common to omit $(x,y)$ throughout. Then our formula $$\varphi^1=Adx+Bdy,$$ suggests another meaning of $dx,dy$. Consider, $\varphi^1$ "looks" like a linear combination of $dx,dy$. Then, $\{dx,dy\}$ "is" a basis of $\Omega^1(R)$!
Of course, since $A,B$ are functions, this is not a linear combination we know from linear algebra. However, if we fix a location, it is!
So, $$\Omega^1(p)=span\{dx,dy\}.$$
Exercise. Prove this formula.
For $2$-forms we will need the wedge product.