Realizations of cubical complexes

Redirect to:

• Cubical complexes

We want to understand the point-set topology of cubical complexes.

Let's start with the cells. The cells of a cubical complex are simply subsets of the Euclidean space and below they are treated as such. So, we can study their openness, closedness (see Open and closed sets, interior, frontier and closure (see Classification of points with respect to a subset).

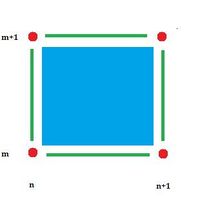
In dimension $2$, we have $$\begin{array}{l|l} 0{\rm -cell}, {\rm \hspace{3pt} vertex \hspace{3pt}} P & {\rm closed, \hspace{3pt} not \hspace{3pt} open} \\ 1{\rm -cell}, {\rm \hspace{3pt} edge \hspace{3pt}} a & {\rm neither \hspace{3pt} open \hspace{3pt} nor \hspace{3pt} closed} \\ 2{\rm -cell}, {\rm \hspace{3pt} face \hspace{3pt}} \sigma & {\rm open, \hspace{3pt} not \hspace{3pt} closed} \end{array}$$

Also, $$\begin{array}{l} {\rm Int}(P) = \emptyset, {\rm Fr}(P) = P, {\rm Cl}(P) = P \\ {\rm Int}(a) = \emptyset, {\rm Fr}(a) = a, {\rm Cl}(a) = a \cup \{ {\rm the \hspace{3pt} two \hspace{3pt} endpoints} \} \\ {\rm Int}(\sigma) = \sigma, \\ {\rm Fr}(\sigma) = \displaystyle\cup \{4 {\rm \hspace{3pt} edges \hspace{3pt} and \hspace{3pt}} 4 {\rm \hspace{3pt} vertices \hspace{3pt} of \hspace{3pt} the \hspace{3pt} square} \}, \\ {\rm Cl}(\sigma) = {\rm the \hspace{3pt} closed \hspace{3pt} square} \end{array}$$

It is important to distinguish the frontier of a cell if it treated as as a subset from the boundary of the cell if treated as a chain. Certainly the former is a subset and the latter is another chain, i.e., an algebraic entity. But even when we can go back and forth between the sets and algebra, the difference is still dramatic:

$$\begin{array}{l|l} {\rm Fr}(P) = P & \partial P = 0 \\ {\rm Fr}(a) = a & \partial a = {\rm the \hspace{3pt} sum \hspace{3pt} of \hspace{3pt} the \hspace{3pt} two \hspace{3pt} endpoints} \\ {\rm Fr}(\sigma) = \displaystyle\cup \{4 {\rm edges \hspace{3pt} and \hspace{3pt}} 4 {\rm \hspace{3pt} vertices} \} & \partial \sigma = {\rm the \hspace{3pt} sum \hspace{3pt} of \hspace{3pt}} 4 {\rm edges} \end{array}$$

As you can see in the latter case it is the dimension of the cells that matters not the dimension of the ambient space.

Recall that a cubical complex is a collection of cells with: if a cell belongs to the complex then so does any of its boundary cells, and its realization $|K|$ is the union of all of its cells.

A complex and its realization:

It follows that:

Theorem. $|K|$ is a closed subset of ${\bf R}^n$.

Proof. In dimension $2$: $\blacksquare$

It follows that

Theorem. If $K$ is finite, $|K|$ is compact.

Why do we need realizations? If we want to study the topology of a subset of the Euclidean space, we can do that by representing it as a realization of a cubical complex:

Given $A \subset {\bf R}^n$, find a cubical complex $K$ such that $|K| = A$, evaluate its homology, then set $H(A) = H(K)$.

It is possible that $A = |K| = |L|$ for another complex $L$. However, $H(K) = H(L)$, see Invariance of homology.