This site is being phased out.
Precalculus with Scientific Applications -- Spring 2016 -- final exam
Name:_________________________ $\qquad$ 14 problems, 140 points total
- Justify every step you make with as thorough an explanation as possible, in English.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1. Represent this function: $h(x)=\tan (2x)$ as the composition of two functions of variables $x$ and $y$.
$\bullet$ 2. Functions $y=f(x)$ and $u=g(y)$ are given below by tables of some of their values. Present the composition $u=h(x)$ of these functions by a similar table: $$\begin{array}{c|c|c|c|c} x &0 &1 &2 &3 &4 \\ \hline y=f(x) &1 &1 &2 &0 &2 \end{array}$$ $$\begin{array}{c|c|c|c|c} y &0 &1 &2 &3 &4 \\ \hline u=g(y) &3 &1 &2 &1 &0 \end{array}$$
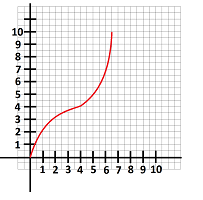
$\bullet$ 3. Find the average rate of change of the function shown below on the interval $[1,6]$:
$\bullet$ 4. Solve the equation: $2^x=3^{x+1}$. Don't simplify.
$\bullet$ 5. By transforming the graph of $y=\sin x$, plot the graph of the function $f(x)=2\sin (x-3)$. Identify the domain, the range, and the asymptotes.
$\bullet$ 6. A city loses $3\%$ of its population every year. How long will it take to lose $20\%$?
$\bullet$ 7. Give examples of an even function, an odd function, and a function that's neither. Provide formulas.
$\bullet$ 8. Make a hand-drawn sketch of the graph of the function: $$f(x)= \begin{cases} -3 &\text{ if } x<0\\ x^2 &\text{ if } 0\le x<1\\ x &\text{ if } x>1 \end{cases}$$
$\bullet$ 9. Find the composition $h(x)=(g\circ f)(x)$ of the functions $y=f(x)=x^{2}-1$ and $g(y)=3y-1.$ Evaluate $h(1).$
$\bullet$ 10. Suppose $f$ is a polynomial of degree $55$ and its leading term is $-1$. Describe the long term behavior of this function.
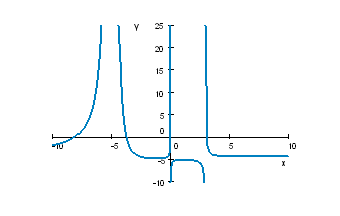
$\bullet$ 11. The graph of the function $y=f(x)$ is given below. (1) Find its domain. (2) Determine intervals on which the function is decreasing or increasing. (3) Provide $x$-coordinates of its relative maxima and minima. $(4)$ Find its asymptotes.
$\bullet$ 12. Given vectors $a=<1,2>,\ b=<-2,1>$, find their magnitudes and the angle between them.
$\bullet$ 13. Compute $\displaystyle\sum _{n=1}^{4} n^2$.
$\bullet$ 14. Find the equation of the line starting at the point $(1,2,3)$ in the direction of the vector $<1,1,1>$.