Examples of homology of cubical complexes

Redirect to:

• Oriented chains

Let's construct a cubical complex for the disjoint union of a circle and an line segment and compute its homology, $X$.

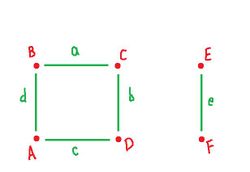
The simplest way to capture the topology of $X$ is by considering a square and an edge as on the right. Its cubical representation includes $5$ edges and $5$ vertices. We name them as shown.

More specifically below we present the cubical complex $K$ of $X$:

• Part $1$, list of all cells:
  • $0$-cells: $\{A, B, C, D, E, F \}$
  • $1$-cells: $\{a, b, c, d, e \}$
• Part 2, list of the boundaries of all cells:
  • $0$-cells: ${\partial}A = 0, {\partial}B = 0, {\partial}C = 0, {\partial}D = 0, {\partial}E = 0, {\partial}F = 0$
  • $1$-cells: ${\partial}a = B + C, {\partial}b = C + D, {\partial}c = D + A, {\partial}d = A + B, {\partial}e = E + F$

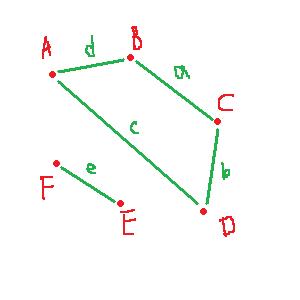
As an exercise let's reconstruct $X = |K|$ from $K$. First we randomly throw the $0$-cells (Part 1) on the plane:

(This is called the $0$-skeleton of $K$.)

Then we add the $1$-cells (Part 1) according to their boundaries (Part 2):

This is the $1$-skeleton of $K$.

The outcome is different from $X$ but homeomorphic to it. Note that if the order of $0$-cells was different, we'd have to put them in 3D space to avoid intersections of cells. This is possible for any complex if we choose the ambient space of high enough dimension.

Next we compute the homology. First dimension $0$. From the boundaries of $1$-cells (Part 2) we know:

$$B \sim C, C \sim D, D \sim A, A \sim B, E \sim F.$$

Therefore we have two equivalence classes:

$[A] = \{A, B, C, D \}$ and $[E] = \{E, F \}$,

as well as their sum. So, the homology group $H_0(K)$ of $K$ is generated by these two classes:

$$H_0(K) = <[A], [E]>.$$

Now dimension $1$. From examination of the boundaries of $1$-cells, ones sees that the only non-zero $1$-cycle is $q = a + b + c + d$. Now, since there are no $2$-cells, this cycle isn't homologous to $0$. So,

$$H_1(K) = <[q]>.$$

Thus the Betti numbers are $2$ and $1$.

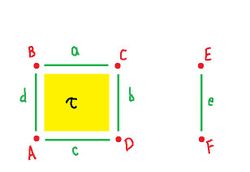
Further, what happens if there is a $2$-cell $\tau$ on the left?

This is the new complex:

• Part $1$, list of all cells:
  • $0$-cells: $\{A, B, C, D, E, F \}$
  • $1$-cells: $\{a, b, c, d, e \}$
  • $2$-cells: $\{ \tau \}$
• Part 2, list of the boundaries of all cells:
  • $0$-cells: ${\partial}A = 0, {\partial}B = 0, {\partial}C = 0, {\partial}D = 0, {\partial}E = 0, {\partial}F = 0 $
  • $1$-cells: ${\partial}a = B + C, {\partial}b = C + D, {\partial}c = D + A, {\partial}d = A + B, {\partial}e = E + F$
  • $2$-cells: ${\partial} \tau = a + b + c + d = q$

Then there are no changes in dimension $0$:

$$H_0(K) = <[A], [E]>.$$

And in dimension $1$ the only non-zero cycles, $q$, is now homologous to $0$, so $$H_1(K) = 0.$$

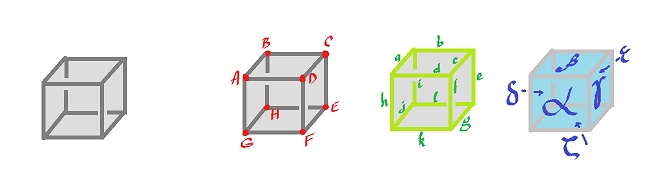
This is a cube (empty), i.e., a topological sphere.

The list of cell is already given. To present the cubical complex, write the boundaries.

Exercise. Compute its homology.