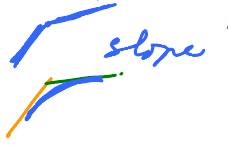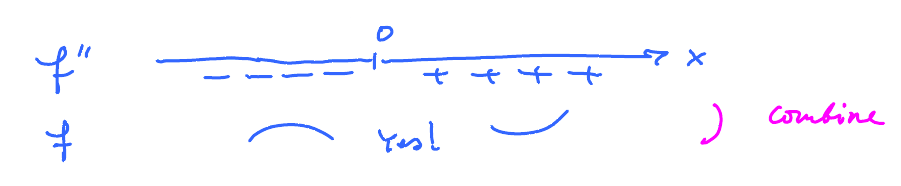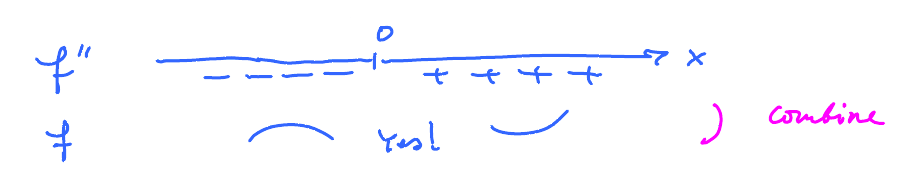Using derivative to study concavity

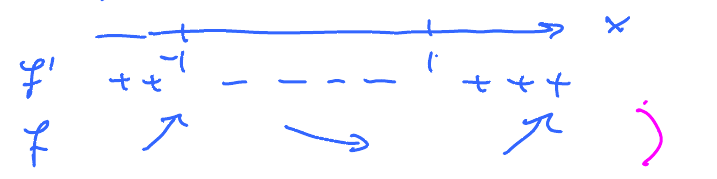
Recall how we are using derivative to study monotonicity.

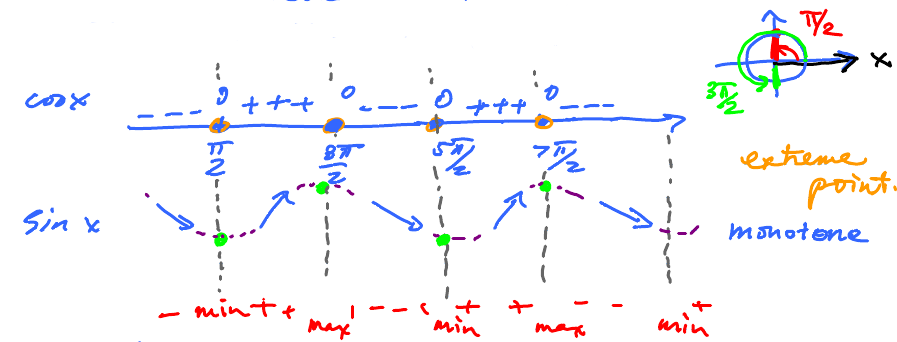
Consider $$\begin{alignat}{3} f(x) &= \sin x & \quad & \nearrow & \quad & \searrow \\ f^{\prime}(x) &= \cos x & \quad & + & \quad & - \end{alignat}$$

Start with with equations: $\cos x = 0, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots$.

That's not all. Derivatives give us more than just $\nearrow\searrow$.

Consider this common situation:

 "the growth of the economy has slowed down". 

Suppose $f$ is the volume of the economy. What does the above statement tell us about the rate of growth, $f^{\prime}$, of the economy?

Translated: the growth of the derivative has slowed down! But the growth is described by the derivative!

We are talking about the derivative of the derivative. So this is about $ f^{\prime\prime}$.

Recall $f^{\prime\prime} = (f^{\prime})^{\prime}$.

Then if $ f^{\prime} \searrow $ then $f^{\prime\prime} < 0$.

Two main possibilities when $f^{\prime\prime} < 0$:

Now, what if the economy grew during the year: $f \nearrow$. Again, there are two main possibilities. For example...

During the first half, the growth was increasing, which means that the economy was accelerating.

During the second half, the growth was decreasing, which means that the economy was decelerating.

This is then the big picture:

The geometry is clear, what so we do to find out algebraically?

In fact, we need to answer: What happens to tangent lines?

Observation:

1. They turn counter clockwise, so
2. the slope has increased.

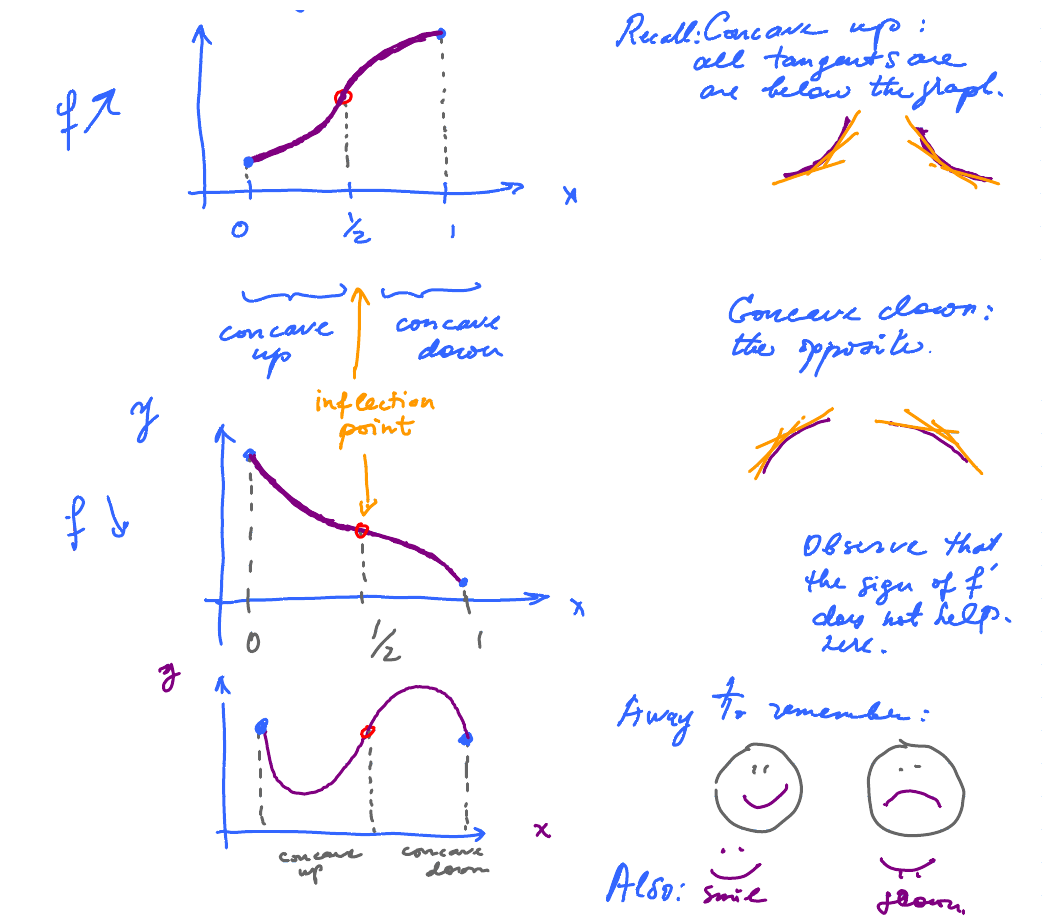
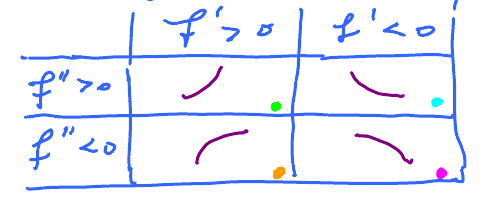
This is concave up and opposite for concave down:

$f^{\prime}$ has increased, or $$(f^{\prime})^{\prime} > 0$$ or $$ f^{\prime\prime} > 0. $$

Concavity Theorem. Suppose $f$ is twice differentiable. Then

• if $f^{\prime\prime}(x) > 0$ on interval $(a,b)$ then $f$ is concave up on $(a,b)$;
• if $f^{\prime\prime}(x) < 0$ on interval $(a,b)$ then $f$ is concave down on $(a,b)$.

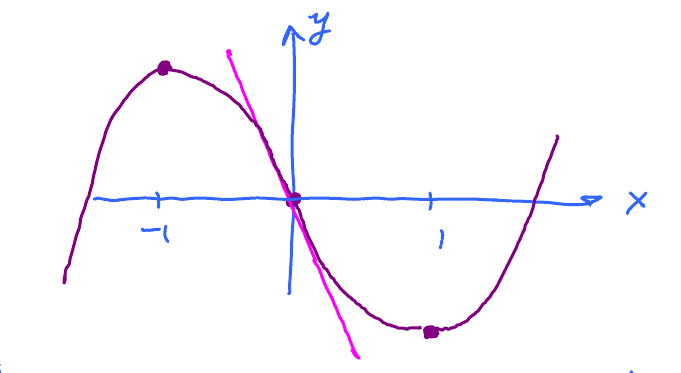
Example. Suppose $$\begin{aligned} f(x) &= x^{3} - 3x \\ f^{\prime}(x) &= 3x^{2} - 3 \end{aligned}$$ Critical point: $x = \pm 1$

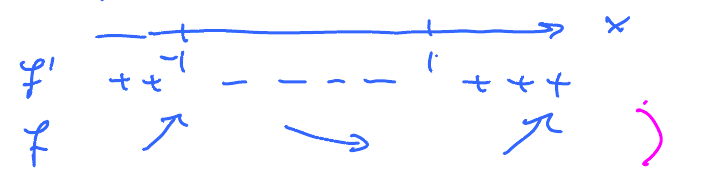
Just follow the arrows to get a rough sketch:

Look at the points where $f^{\prime\prime}$ changes its sign: $$f^{\prime\prime}(x) = 6x,$$ solve for $x$: $$x = 0.$$

Combine the tables:

Reading from this table we draw a better picture:

What about a different kind of problem: identify the extreme points of the function.

Turns out: concavity helps!

Suppose we have already found a critical point: $f^{\prime} = 0$.

It possibly can be:

• Local Max : (concave down)
• Local Min : (concave up)
• Neither : (inflection)

Generally...

Second Derivative Test. Given a point $c$ with $f^{\prime}(c) = 0$$.

• If $f^{\prime\prime}(c) < 0$, then $c$ is a local max point.
• If $f^{\prime\prime}(c) > 0$, then $c$ is a local min point.
• Extra: If $f^{\prime\prime}(c) = 0$, then test fails.

Possibilities:

Max/Min: $$ f(x) = x^{4} \to f^{\prime\prime}(0) = 0 $$

Neither: $$ f(x) = x^{3} \to f^{\prime\prime}(x) = 6x $$

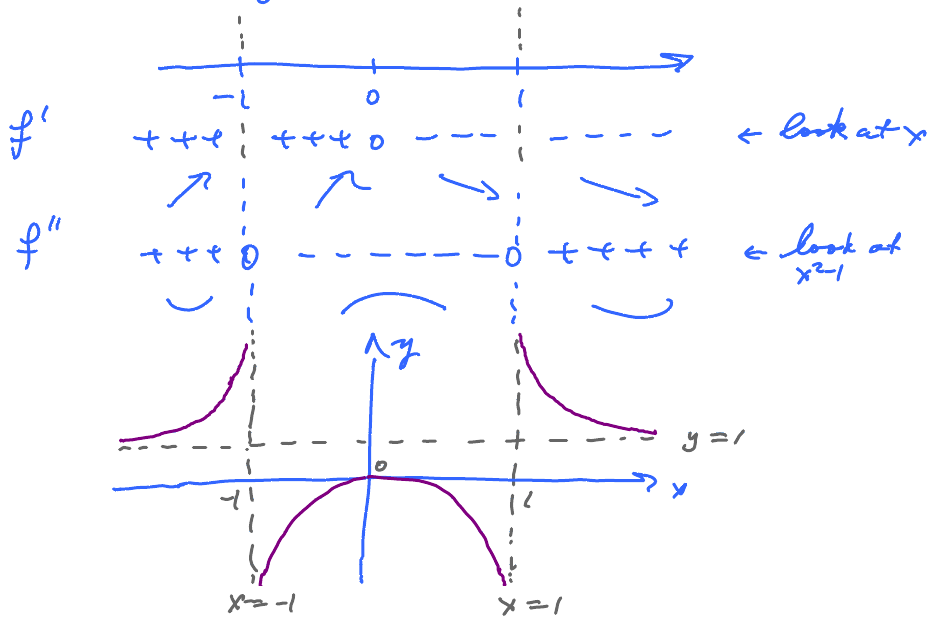
Exercise. Let $$f(x) = \frac{x^{2}}{x^{2} - 1}.$$ Domain all but $x = \pm 1 $. (Note: this is not a critical point as $f$ is undefined here.)

• Vertical Asymptotes : $$ x = 1, x = -1. $$
• Horizontal Asymptotes : $$ y= 1. $$

Now compute the derivatives. $$\begin{aligned} f^{\prime} &= \frac{2x(x^{2} - 1) - x^{2}\cdot 2x}{(x^{2} - 1)^{2}} \\ &= \frac{2x^{3} - 2x - 2x^{3}}{(x^{2} - 1)^{2}} \\ &= - \frac{2x}{(x^{2} - 1)^{2}} \end{aligned}$$ We had to simplify in order to differentiate again. $$\begin{aligned} f^{\prime\prime}(x) &= -\frac{2(x^{2} - 1)^{2} - 2x \cdot 2(x^{2} - 1) 2x}{(x^{2} - 1)^{4}} \\ & = - \frac{2(x^{2} - 1)(x^{2} - 1 - 4x^{2})}{(x^{2} - 1)^{4}} \\ & = \frac{2(x^{2} - 1)(3x^{2} + 1)}{(x^{2} - 1)^{4}} = 0 \end{aligned}$$ We had to simplify in order to factor.

Find the signs of the factors and the derivatives:

The way the graph approaches the asymptotes can be understood now from $\nearrow\searrow$ behavior of $f$: $$\lim_{x \to -1^{-}} f(x) = + \infty, \quad \lim_{x \to -1^{+}} f(x) = -\infty, \ldots $$

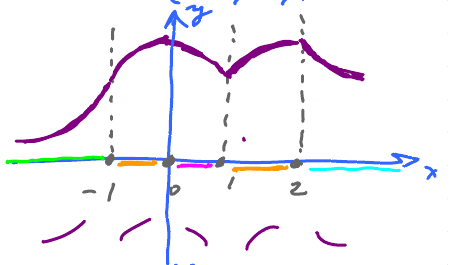
Example. An opposite problem... Plot $f$ with

• $f^{\prime} > 0$ on $(-\infty,0)$ and $(1,2)$.
• $f^{\prime} < 0$ on $(0,1)$ and $(2,\infty)$.
• $f^{\prime\prime} > 0$ on $(-infty,-1)$ and $(2,\infty)$.
• $f^{\prime\prime} < 0$ on $(-1,2)$.

This is how $f^{\prime}$, $f^{\prime\prime}$ relate to the shape of the graph.