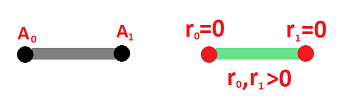This site is being phased out.
Simplicial complexes
Contents
From graphs to multi-graphs
A graph is pure data. It consists of two sets:
- the nodes, say, $N=\{A, B, C, D\}$, representing some agents, and
- the edges, say, $E=\{AB, BC, CA, DA, CD\}$, representing some pairwise relation between them.
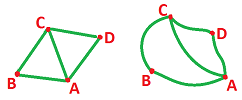
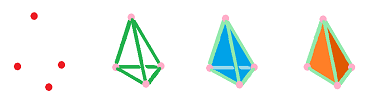
The topology is hidden in the data and, in order to see it, we often have to illustrate the data by a subset of the Euclidean space, as follows. Each node is plotted as a distinct point, but otherwise arbitrarily, and these points are connected by simple curves (paths) that can have only the nodes in common:
This set is called a realization of the graph, which is no more than an illustration of the data. Unfortunately, illustrations are only revealing when the data they represent is small...
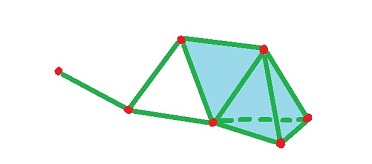
Now, with a graph on the left, what could be the meaning of the data behind the picture on the right?
There must be some new kind of relation present! This three-way relation exists for $A,B,C$ but not for $A,C,D$.
We now have a collection $K$ of three sets:
- the nodes $N=\{A, B, C, D\}$ representing some agents,
- the edges $E=\{AB, BC, CA, DA, CD\}$ representing some pairwise relations, and
- the triangular face(s) $F=\{ABC\}$ representing some three-way relations.
This data set is called a simplicial complex (or sometimes even a “multi-graph”). Its elements are called $0$-, $1$-, and $2$-simplices.
Example (graph). The graph $G$ may come from a series of phone conversation between the four individuals: $$\begin{array}{c|cccccc} & A &B &C &D \\ \hline A: &- &+ &+ &+\\ B: &+ &- &+ &-\\ C: &+ &+ &- &+\\ D: &+ &- &+ &-. \end{array}$$ Here, the fact that a conversation has occurred, it is marked with “+”.
$\square$
Example (simplicial complex). Meanwhile, the simplicial complex $K$ above may come from, say, the list of stores visited by these individuals: $$\begin{array}{c|cccccc} & K &M &J &W \\ \hline A: &+ &+ &+ &-\\ B: &+ &- &- &- \\ C: &+ &+ &- &+\\ D: &- &- &+ &+. \end{array}$$ Here, 'K' may stand for Kroger, 'M' for Macy's, 'J' for JCPenney, and 'W' for Walmart.
$\square$
Exercise. Create a similar table for yourself and four of your best friends documenting your joint activities. Create a simplicial complex.
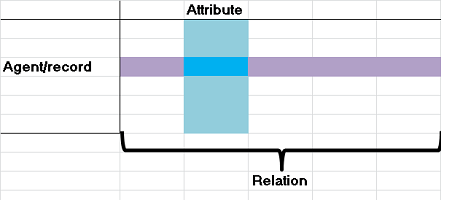
Example (database). A similar construction is possible for any “relational database”, which is simply a table:
For a single column table, every collection of $n$ agents that happen to have an identical attribute form an element of our simplicial complex, an $(n-1)$-simplex.
$\square$
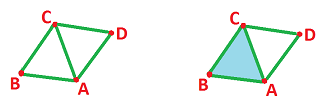
Based on these examples, it seems that a simplicial complex is nothing but a collection of subsets of some finite set. However, anticipating the need for defining the boundaries of simplices, we want all the boundary cells of each simplex to be present as well. These cells are called faces of the simplex. For example, the $1$-faces of $ABC$ are $AB,BC,CA$ and the $0$-faces are $A,B,C$. This is the notation we will use:
- for $\tau,\sigma \in K$, we write $\sigma < \tau$ if $\sigma$ is a face of $\tau$.
But this means simply that $\sigma$ is a subset of $\tau$: $$\sigma < \tau \Leftrightarrow \sigma \subset \tau.$$
An examination of this definition reveals the following properties:
- if $\tau \in K$ and $\sigma < \tau$ then $\sigma \in K$;
- if $\tau, \sigma \in K$ then $\tau \cap \sigma < \tau$.
These properties are reflected in a realization of this simplicial complex:
- the complex contains all faces of each simplex;
- two simplices can only share a single face.
Not every list of subsets of $S$ would work then. Consider $\{AB, BC \}$ for example. This can't be a simplicial complex because the $0$-faces of these $1$-simplices are absent. However, once we add those to the list, the first condition of simplicial complex above is satisfied and the second too, automatically. Indeed, the list becomes: $$\{AB, BC, A, B, C\}.$$
So, as it turns out, the first condition is the only one we need to verify.
Definition. A collection $K$ of subsets of a finite set $S$ is called an abstract simplicial complex if all subsets of any element of $K$ are also elements of $K$, i.e.,
A subset with exactly $n+1$ elements, $n=0,1,...$, is called an $n$-simplex.
Exercise. (a) Demonstrate that a relational database with a single attribute produces a simplicial complex as described above. (b) Give an example how simplices (and a simplicial complex) can be formed without requiring the attributes to be identical. (c) How is a complex formed if there are more than one attribute?
Simplices in the Euclidean space
Next, we consider realizations of simplicial complexes as a way of giving them a topology. We start with simplices.
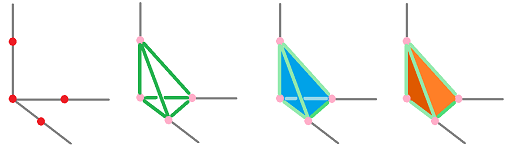
The most direct way to represent an $n$-simplex is as a “polytope” in ${\bf R}^n$ the $n+1$ vertices of which are located at the end-points of the basis vectors of the $n$-dimensional Euclidean space and zero: $$\begin{array}{cccc} (0,0,0,0,...,0,0,0),\\ (1,0,0,0,...,0,0,0), \\ (0,1,0,0,...,0,0,0), \\ ...\\ (0,0,0,0,...,0,1,0),\\ (0,0,0,0,...,0,0,1). \end{array}$$ A $3$-simplex built this way is illustrated below:
Alternatively, we can use the first $n$ basis vectors of the $N$-dimensional Euclidean space with $N\ge n$. Suppose such a space is given.
Now, we will build a similar object starting with an arbitrary collection of points:
Given a set of $n+1$ points $\{A_0, A_1 , ... , A_n\}$, a convex combination of these points is any point $x$ given by $$x= \sum_{i=0}^n \lambda_i A_i,$$ with the real coefficients that satisfy:
- 1. $0\le \lambda_i\le 1, \ \forall i$, and
- 2. $\sum_i \lambda_i=1.$
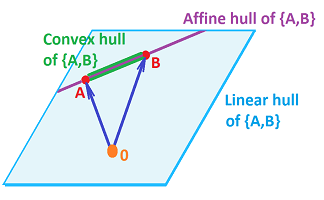
Then the convex hull is the set of all convex combinations.
These two conditions are important. To illustrate the idea, let's compare the convex hull of two points in ${\bf R}^3$ to
- the linear hull (aka the span) -- no restrictions on the coefficients, and
- the affine hull -- only the second restriction left.
They are show below:
The convex hull of this finite set is denoted by $$\operatorname{conv}\{A_0, A_1,..., A_n \},$$ and the convex hull of any set $Q$ is the set of all of its convex combinations: $$\operatorname{conv}(A):=\bigcup \{ \operatorname{conv}(P):\ P\subset Q, P \text{ finite}\}.$$
Recall that a set $Q$ is convex if it contains all of its pairwise convex combinations: $$\lambda x+(1-\lambda)y \in Q,\ \forall x,y \in Q,0\le\lambda\le 1.$$ It follows that for any convex set $Q$ we have $$\operatorname{conv}(Q)=Q.$$ Convex sets are important in topology because they are “acyclic”: they are connected, have no holes, voids, etc.
That's why it is a good idea to choose the building blocks to be convex, just as the ones of cubical complexes. But we also want to control the dimensions of these blocks!
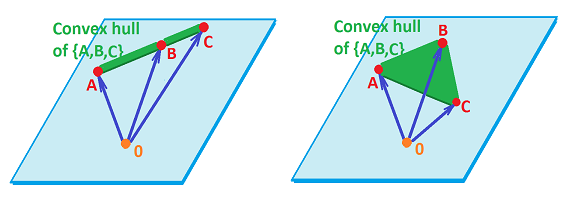
This is the reason why we need a condition that prevents a “degenerate” situation when, for example, the convex hull of three points isn't a triangle, such as this: $$\operatorname{conv}\{(0,0),(1,0),(2,0)\}.$$ Below the issue is illustrated in ${\bf R}^3$:
We require these $n+1$ points $\{A_0, A_1 , ... , A_n\}$ to be in general position, which means:
One may say that this is a generic arrangement in the sense that if you throw three points on the plane, the probability that they line up is zero. They are also called “geometrically independent”.
Proposition. The affine hull $$\left\{\sum_{i=0}^n r_iA_i:\sum_ir_i=1\right\}$$ of $n+1$ points in general position is an $n$-dimensional affine subspace (i.e., $M=v_0+L$, where $L$ is a linear subspace and $v_0$ is some vector).
Definition. A geometric $n$-simplex is defined as the convex hull of $n+1$ points $A_0, A_1, ..., A_n$ in general position: $$s:=A_0 A_1 ... A_n := \operatorname{conv}\{A_0, A_1, ..., A_n \}.$$
Exercise. Prove that the order of vertices doesn't matter.
Suppose $s$ is an $n$-simplex: $$s=A_0 ... A_n .$$ An arbitrary point in $s$ is a convex combination of the vertices: $$x=\sum_i r_iA_i:\sum_ir_i=1,\ r_i\ge 0, \forall i.$$ These coefficients $r_0 ,...,r_n$ are called the barycentric coordinates of $x$.
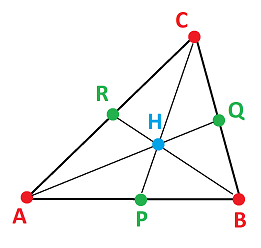
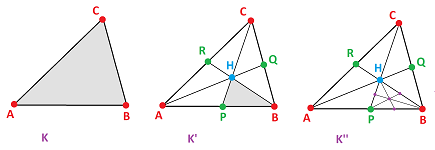
Example. An example of dimension $2$ is below:
Here:
- $P=\frac{1}{2}A+\frac{1}{2}B,Q=\frac{1}{2}B+\frac{1}{2}C,R=\frac{1}{2}C+\frac{1}{2}A,$
- $H=\frac{1}{3}A+\frac{1}{3}B+\frac{1}{3}C.$
$\square$
Exercise. Prove that the barycentric coordinates are unique for any given point.
Then it makes sense to write: $$\begin{array}{llll} A=(1,0,0),&B=(0,1,0),&C=(0,0,1);\\ P=\left( \frac{1}{2},\frac{1}{2},0 \right), & Q=\left( 0,\frac{1}{2},\frac{1}{2} \right), & R=\left( \frac{1}{2},0,\frac{1}{2} \right);\\ H=\left( \frac{1}{3},\frac{1}{3},\frac{1}{3} \right). \end{array}$$
Exercise. Show that the point with barycentric coordinates $(1/3,1/3,1/3)$ is the center of mass of the triangle.
The point with equal barycentric coordinates is called the barycenter of the simplex.
Theorem. The $n$-simplex is homeomorphic to the $n$-ball ${\bf B}^n$.
Exercise. Prove the theorem.
Realizations
The realizations of simplices up to dimension $3$ are simple topological spaces:
Just as realizations of cubical complexes, a realization of a simplicial complex $K$ is made of cells, but instead of
- edges, squares, cubes, ..., $n$-cubes;
they are
- edges, triangles, tetrahedra, ..., $n$-simplices:
Definition. A geometric simplicial complex is a finite collection of points in space along with some of the geometric simplices defined by them. We will refer by the same name to the union of these simplices. Topological spaces homeomorphic to geometric simplicial complexes are called polyhedra.
A geometric complex acquires its topology from the ambient Euclidean space. But how do we study its homology?
There is an additional structure here; a simplex has faces.
Example (dimension 1). Suppose $a$ is a $1$-simplex, $$a = A_0A_1 .$$ Then its faces are the vertices $A_0$ and $A_1$. They can be easily described algebraically. An arbitrary point in $a$ is a convex combination of $A_0$ and $A_1$: $$x=r_0A_0 + r_1A_1 \text{ with } r_0 + r_1 = 1,\ r_0,r_1\ge 0.$$ What about $A_0$ and $A_1$? They are convex combinations too but of a special kind: $$A_0 = r_0A_0 + r_1A_1 \text{ with } r_0 = 1, r_1 = 0,$$ $$A_1 = r_0A_0 + r_1A_1 \text{ with } r_0 = 0, r_1 = 1.$$
$\square$
In other words,
Notation. We write
- $\sigma < \tau$ if $\sigma$ is a face of $\tau$.
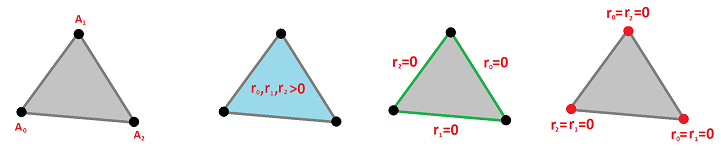
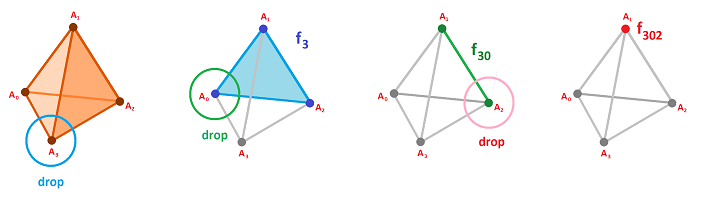
Example (dimension 2). Suppose $\tau$ is a $2$-simplex, $$\tau = A_0A_1A_2 .$$ An arbitrary point in $\tau$ is a convex combination of $A_0,A_1,A_2$: $$x=r_0A_0 + r_1A_1 + r_2A_2 \text{ with } r_0 + r_1 + r_2 = 1,\ r_i\ge 0.$$ To find all $1$-faces, set one of these coefficients equal to $0$; the brackets indicate which: $$f_2 :=A_0A_1[A_2]= \{r_0A_0 + r_1A_1 + r_2A_2: r_0 + r_1 + r_2 = 1, r_2 = 0\},$$ $$f_1 :=A_0[A_1]A_2= \{r_0A_0 + r_1A_1 + r_2A_2: r_0 + r_1 + r_2 = 1, r_1 = 0\},$$ $$f_0 :=[A_0]A_1A_2= \{r_0A_0 + r_1A_1 + r_2A_2: r_0 + r_1 + r_2 = 1, r_0 = 0\}.$$
So, $$f_0,f_1,f_2 < \tau.$$
To find all $0$-faces, set two of these coefficients equal to $0$: $$A_0 =f_{12}=A_0[A_1][A_2]= 1 \cdot A_0 + 0 \cdot A_1 + 0 \cdot A_2, {\rm \hspace{3pt} etc}. $$
$\square$
Similar ideas apply to higher dimensions as we drop vertices one by one from our convex combinations.
Notation. For each $k=0,1,...,n$, we denote by $f_k$ the $k$th face of $s$ which is an $(n-1)$-simplex acquired by setting the $k$th barycentric coordinate equal to $0$: $$f_k:=A_0 ... [A_k] ... A_n=\left\{\sum_i r_iA_i:\sum_ir_i=1,r_i\ge 0,r_k=0\right\}.$$ This way the $k$th vertex is removed from all convex combinations. Further, for each pair $i,j=0,1,...,n,\ i \ne j$, let $f_{ij}=f_{ji}$ be the $(n-2)$-simplex acquired by setting the $i$th and $j$th barycentric coordinates equal to $0$: $$f_{ij}:=A_0 ... [A_i] ... [A_j] ... A_n.$$ This way the $i$th and $j$th vertices are removed from all convex combinations.
Exercise. Show that $f_{ij}$ is a face of $f_i$ and a face of $f_j$.
We can continue this process and drop more and more vertices from consideration. The result is faces of lower and lower dimensions.
Definition. Given an $n$-simplex $\tau$, the convex hull $f$ of any $m+1, m<n$, vertices of $\tau$ is called an $m$-face of $\tau$. We write: $f < \tau$.
Exercise. How many $m$-faces does an $n$-simplex have?
Definition. The boundary of a geometric $n$-simplex is the union of all of its $(n-1)$-faces.
This union can be seen as either:
- the formal binary sum, or
- a linear combination with real coefficients.
In that latter case, it is a combination of all of the $(n-1)$-faces of the simplex in the original abstract simplicial complex. Then, the boundary operator can be defined and the rest of the homology theory can be developed. Of course, we will rather carry out this construction with the abstract simplicial complexes themselves.
Meanwhile, the topological issues, as opposed to the geometrical issues, of realizations of simplicial complexes will be discussed later under cell complexes:
Refining simplicial complexes
Definition. The Euler characteristic $\chi (K)$ of an $n$-dimensional simplicial complex $K$ is defined as the alternating sum of the number of simplices in $K$ of each dimension: $$\chi (K) = \# 0 \text{-simplices } - \# 1\text{-simplices } + \# 2\text{-simplices } - ... \pm \# n\text{-simplices.}$$
We will prove later that the Euler characteristic is a topological invariant, i.e., if complexes $K$ and $M$ have homeomorphic realizations, $|K| \approx |M|$, then their Euler characteristics coincide, $\chi(K) = \chi(M)$. The converse of this theorem is not true, which means that the Euler characteristic is not a “complete topological invariant”.
Exercise. Find examples of non-homeomorphic complexes (of dimensions $1,2,3$) with the same Euler characteristic.
We will provide evidence in support of this theorem:
This is what “elementary subdivisions” of a $2$-dimensional complex do to its Euler characteristic:
- Adding a vertex, $+1$, in the middle of an edge will split the edge and, therefore, increase the number of edges by one, $-1$.
- When this edge is in the boundary of a face, an extra edge has to be added, $-1$, but the face is also split in two, $+1$.
- Adding a vertex in the middle of a face, $+1$, will require $3$ more edges, $-3$, and the face split into three, $-2$.
In all three cases the net effect on the Euler characteristic is nil.
Exercise. Provide a similar analysis for a $3$-simplex.
Exercise. What is the analog of barycentric subdivision for cubical complexes? Provide a similar analysis for $2$-dimensional cubical complexes.
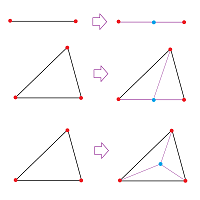
There is a standard method for refining geometric simplicial complexes of all dimensions. First, we cut every $n$-simplex into a collection of $n$-simplices, as follows. The process is inductive, for $k=0,1,2,...$. For each $k$-simplex $\tau \in K$,
- we remove $\tau$ and all of its boundary simplexes (except for the vertices) from $K$;
- we add a vertex $V_{\tau}$ to $K$, and then
- we create a new simplex from $V_{\tau}$ and each boundary simplex $a$ of $\tau$.
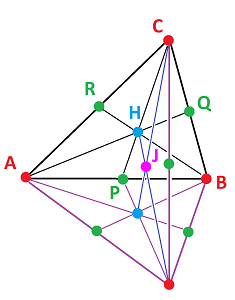
Example (dimension 2). The result is a new collection $K'$ of simplices. This is what it looks like in dimension $2$:
Here:
- for $\tau =ABC$ we choose $V_{\tau}=H$;
- for $\tau =AB$ we choose $V_{\tau}=P$;
- for $\tau =BC$ we choose $V_{\tau}=Q$;
- for $\tau =AC$ we choose $V_{\tau}=R$;
We also add the new edges: $AP,PB,PH$, etc., and new faces: $AHP,PHB$, etc.
$\square$
Exercise. Prove that the new collection is a simplicial complex.
A specific version of this operation is called the barycentric subdivision: the new vertex $V_{\tau}$ chosen for each cell $\tau$ is its barycenter -- the point with equal barycentric coordinates -- of the cell.
Example (dimension 3). The structure of the subdivision of a $3$-simplex is more complex:
For the $3$-simplex above, we:
- keep the $4$ original vertices,
- add $6$ new vertices, one on each edge,
- add $4$ new vertices, one on each face, and
- add $1$ new vertex inside the simplex.
Then one adds many new edges and faces.
$\square$
Exercise. Given an abstract simplicial complex $K$, define a discrete version of barycentric subdivision. Hint: the vertices of the new complex are the simplices of $K$.
The following important result suggested by this analysis is to be proven later.
Theorem (Invariance of Euler characteristic). The Euler characteristic is preserved under barycentric subdivision, i.e., if $K'$ is the simplicial complex that results from the barycentric subdivision of simplicial complex $K$, then $$\chi(K') = \chi(K).$$
Exercise. Prove the theorem (a) for a $3$-dimensional simplicial complex and (b) similarly for a $3$-dimensional cubical complex.
The simplicial complex of a partially ordered set
Suppose $P$ is a finite partially ordered set (poset). We now would like to define a simplicial complex $\Delta (P)$ in such a way that its (Euclidean) topology would well correspond to the order topology on $P$. We will build complex $\Delta (P)$ on this set: its elements become the vertices of $\Delta (P)$ while some of the higher-dimensional cells are also added to mimic the topology of $P$.
The topology is meant to reflect the proximity of the elements of $P$ and this proximity can't rely on any distance. Instead we define the topology of $\Delta (P)$ in terms of the order relation on $P$:
The later means $A<B$ or $A>B$.
Then, in order to encode this fact in $\Delta(P)$, we include an edge between these elements: $$A < B \Rightarrow AB \in \Delta (P).$$ Notice that it doesn't matter how many steps it takes to get from $A$ to $B$!
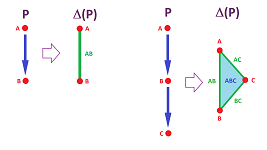
Example. With just two, related, elements present, there is just one edge:
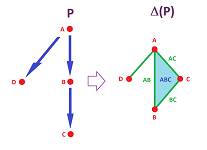
For the second example, we have $P=\{A,B,C:\ A < B < C \}$, and all the pairs $AB,BC,AC$ are present in the complex.
However, the resulting complex has a hole! Such a mismatch of the two topologies is what we want to avoid -- and we add the $2$-simplex $ABC$ to $\Delta (P)$.
$\square$
What does this last simplex have to do with the $1$-simplices we have added so far? All of its vertices are related, pairwise. But this is only possible when they are linearly ordered.
Definition. We define the order complex $\Delta (P)$ of the ordered set $P$ as the simplicial complex on $P$ with all the “monotone sequences” of $P$ as its simplices: $$\Delta (P):=\{A_1 A_2 ... A_n:\ A_i\in P,\ a_1 < a_2 < ... < a_n\},$$
Exercise. Prove that $\Delta(P)$ is a simplicial complex.
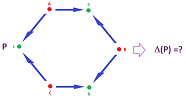
Example.
$\square$
Is it possible to have $\Delta(P)$ with a non-trivial topology?
Exercise. Compute the order complex for the following poset:
Exercise. Indicate what happens to the intervals of the posets in the above examples.
Conversely, the face poset $P(K)$ of a simplicial complex $K$ is the poset of nonempty simplices of $K$ ordered by inclusion.
Exercise. Find the $\Delta(P(S))$, where $S$ is a $2$-simplex.
Exercise. Describe the order topology of $P$ in terms of the simplices of $\Delta (P)$.
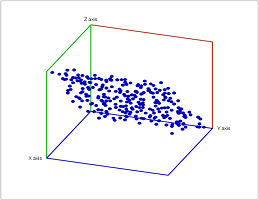
Data as a point cloud
Consider this object:
It appears to be a triple torus.
But what if we zoom in?
We realize that the “object” is just points suspended in space! It is called a point cloud.
Where do point clouds come from? They may come from scanning, as well as radar, sonar, etc. But they also come from data!
If a scientist has conducted $1000$ experiments each of which consists of a sequence of $100$ specific measurements, then the results are combined into a collection of $1000$ disconnected points in ${\bf R}^{100}$. Then the scientist may be looking for a pattern in this data.
It is impossible to visualize higher dimensional data because any representation is limited to dimension $3$ (by using colors one gets $6$, time $7$). In search of a pattern, we might still ask the same questions:
- Is it one piece or more?
- Is there a tunnel?
- Or a void?
- And what about possible $100$-dimensional topological features?
Through “clustering”, statistics answers the first question. The rest need the homology groups of the complex.
This data may hide a “manifold” behind it. It may be a curve (dimension $1$):
or a surface (dimension $2$):
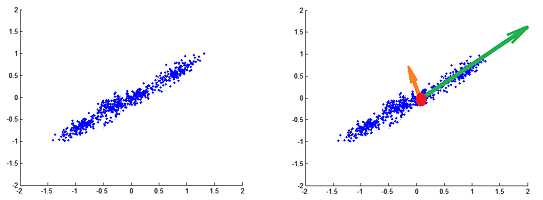
There are some well-developed approaches to this problem. For example, the principal component analysis is a mathematical procedure for finding a linear transformation of the Euclidean space so that the features of the shape of the point cloud are aligned with the new coordinate axes. Such analysis will reveal the interdependence in data:
If the spread along an axis is less than some threshold, this axis may be ignored, which leads to “dimensionality reduction”. However, the linearity assumption of the method may cause it to fail when the manifold is highly curved.
The topological approach is to create a simplicial complex that “approximates” the topological space behind the point cloud.
When the data isn't too noisy, Excel builds a complex by a simple interpolation:
However, the software has to rely on the assumption that this is a surface!
What if the data is noisy? The method is as follows. We pick a threshold $r>0$ so that any two points within $r$ from each other are to be considered “close”. Then we
- add an edge between any two points if they are within $r$ from each other,
- add a face spanning three points if the “diameter” of the triangle is less than $r$, etc.
The result is a simplicial complex that might reveal the topology of whatever is behind the incomplete and noisy data. It is called the Vietoris-Rips complex.
Exercise. For a few values of $r$, construct the Vietoris-Rips complex for: four points on a line, or at the corners of a square, five points at the corners of a pentagon, five random points in the plane, six points at the corners of a cube. Hint: even though the points are in the plane, the complex might be of higher dimension.
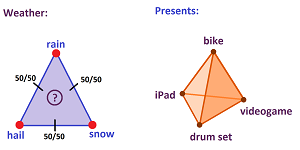
Social choice: the lottery of life
Suppose we are to consider $n+1$ possible events or outcomes, $A_0,...,A_n$. They are conveniently located at the vertices of an $n$-simplex $\sigma ^n=A_0...A_n$.
In addition to these “primary” events, we can also to consider their combinations. Does it make sense to combine them? These events are seen as mutually exclusive but all of them may come true. What happens is determined by the probabilities assigned to the primary events. These convex combinations of primary events are called lotteries, or, in the context of game theory, mixed strategies. The lotteries are conveniently represented by the points of the simplex $\sigma ^n$ and the barycentric coordinates of a point are the probabilities of the lottery. Then $\sigma ^n$ becomes the probability simplex.
Example. The midpoint between “rain” and “snow” represents the lottery when either is equally likely to appear while “hail” is impossible. The probabilites of the three events give the vector $(1/2,1/2,0)$ of barycentric coordinates of this point. $\square$
We next study the preferences of a person among these primary choices and, furthermore, among the lotteries.
The person's set of preferences is given by an order relation on the set of lotteries, i.e., the probability simplex $\sigma^n$. This means, as we know, that the following two axioms are satisfied:
- completeness: for any lotteries $x,y$, exactly one of the following holds:
$$x < y, \ y > x, \ \text{ or } y=x;$$
- transitivity: for any lotteries $x,y,z$, we have:
$$x \le y, \ y \le z \Rightarrow x \le z.$$
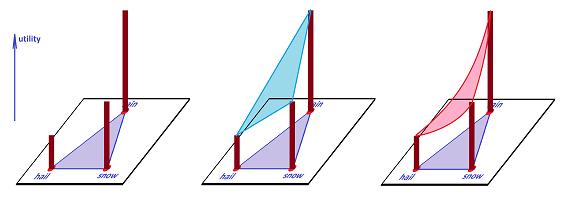
Sometimes these preferences are captured by a single function.
Definition. A utility of a given set of preferences is a function $$u:\sigma ^n\to {\bf R},$$ that satisfies: $$x < y \Leftrightarrow u(x) < u(y).$$
Example. One may prefer: $$rain \ >\ snow\ >\ hail,$$ and define the utility function $u$ by assigning: $$u(r):=3, \quad u(s):=2, \quad u(h):=1.$$ Then, we may evaluate the lotteries by extending $u$ to the whole $2$-simplex, by linearity: $$u(t_1r+ t_2s+t_3h):=t_1\cdot 3+ t_2 \cdot 2+t_3 \cdot 1.$$ Of course, circular preferences, such as $$rain \ > \ snow \ > \ hail \ > \ rain,$$ don't have corresponding utility functions.
$\square$
Under certain special circumstances the preferences can be represented by a utility function of a very simple form -- a linear combination of the utilities of the primary outcomes: $$U(p_0,...,p_n)=\sum_i p_iu_i,$$ where $u_0,..., u_n$ are some numbers. This function is called the expected utility.
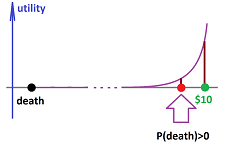
Of course, a person may have preferences that vary non-linearly but it is always assumed that the utility function is continuous.
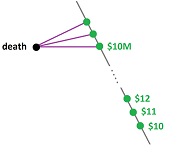
In the study of human behavior, this may present a problem. Even though one would always choose $\$ 10$ over death, the continuity implies that, for a small enough probability $\alpha$, he would see a positive value in the following extreme lottery:
- death: probability $\alpha >0$; and
- $\$ 10$: probability $1-\alpha$.
Exercise. Show that, moreover, such a lottery (with death as a possible outcome) will have a higher utility than that of $\$ 1$, for a small enough $\alpha$.
The reasons why we find this conclusion odd may be that, even though they are clearly comparable, death and $\$ 10$ seem incompatible!
On the other hand, death and $\$ 10$ million may seem compatible to some people and these people would take part in such a lottery.
To account for these observations, we should have an edge between “death” and $\$ 10$M but no edge between “death” and $\$ 10$:
Then, instead of a single simplex, the space of outcomes is a simplicial complex. The complex is meant to capture all possible or plausible lotteries. (Note that one can start with $\$ 10$ and continue gradually, in a compatible fashion, to worse and worse things until reaching death.)
Do we ever face a simplicial complex with a more complex topology, such as one with holes, voids, etc.?
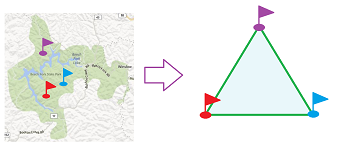
Let's recall the problem of social choice for two hikers: we are to develop a procedure for finding a fair compromise on the location of the camp on the shore of a lake. In the original statement of the problem, the choices of sites are allowed to be arbitrary. However, a simplicial interpretation can be justified too, as follows. Suppose there are three camp sites already set up on the shore of the lake and let's assume that they are the only ones available.
The hiker has a preference location on the shore, but, for the record, he may have to make this choice by assigning an appropriate probability, or weight, to each camp site. For example, if the person's choice is located between camps $A$ and $B$ and twice as close to $A$ than to $B$, then he may assign: $2/3$ to $A$, $1/3$ to $B$, and $0$ to $C$. That sets up a lottery for him. By allowing no more than two non-zero weights, we limit ourselves to the simplicial complex of the hollow triangle. For the original problem, once the aggregation of the choices is completed and the compromise location is chosen, its coordinates are used for a lottery on the whole $2$-simplex. That's the next stage, with which we are not concerned here.
To sum up, we have disallowed some lotteries/mixed strategies in order to prevent the participants from doing some silly things: betting $\$ 10$ against death or placing a camp in the middle of a lake. This decision has produced a space of choices with a possibly non-trivial homology. As we shall see later, this will make impossible some desirable social arrangements.