This site is being phased out.
The algebra of cubical cells
Contents
- 1 Cells as building blocks
- 2 Cubical cells
- 3 Boundaries of cubical cells
- 4 Binary chains and their boundaries
- 5 Are chains just “combinations” of cells?
- 6 Orientations and boundaries
- 7 Computing boundaries with a spreadsheet
- 8 The boundary of a cube in the $N$-dimensional space
- 9 The chain complex of ${\mathbb R}^N$
- 10 The boundary of a boundary is zero
Cells as building blocks
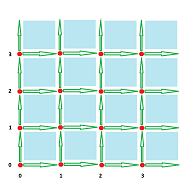
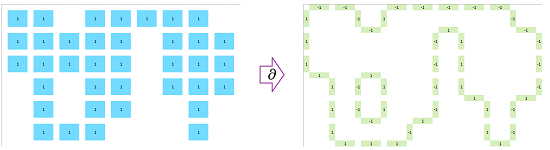
We know that we can decompose the $N$-dimensional Euclidean space into blocks, the $N$-cells. For instance, this is how an object can be represented with tiles, or pixels ($N=2$):
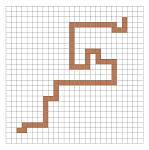
Some questions remain, such as: what about curves? Without making sense of curves we can't study such topological concepts as path-connectedness. Are curves also made of tiles? Such a curve would look like this:
If we look closer, however, this “curve” isn't a curve in the usual sense! The answer is: curves should be made of edges. Then a “discrete” -- but still Euclidean -- curve will look like this:
This idea isn't entirely abstract; just contrast these two images:
The conclusion is that we need to include the lower dimensional cells as additional building blocks. The complete cell decomposition of the pixel is shown below; the edges and vertices are shared with adjacent pixels:
Meanwhile, a mismatch of the dimensions also appears in the $3$-dimensional case if you try to use bricks, or voxels, to make surfaces. Surfaces should be made of faces of our bricks, i.e., the tiles. This is what a “discrete” surface looks like:
It's $2$-dimensional!
The cell decomposition of the voxel follows and here, once again, the faces, edges, and vertices are shared:
One can interpret cells as, literally, the building blocks for everything:
- dimension $1$: sticks and wires;
- dimension $2$: tiles and plywood boards;
- dimension $3$: bricks and logs.
Now, we are on a solid ground to describe adjacency of cells.
Two adjacent edges, $1$-cells, share a vertex, i.e., a $0$-cell:
Two adjacent pixels, $2$-cells, share an edge, i.e., a $1$-cell:
Two adjacent voxels, $3$-cells, share a face, i.e., a $2$-cell:
The hierarchy becomes clear.
Thus, our approach to decomposition of space, in any dimension, boils down to the following:
Cubical cells
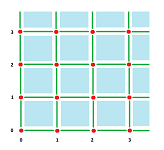
From many possible decompositions of the plane, ${\bf R}^2$, into “cells” we choose the squares:
Here and elsewhere we use the following coloring convention:
- red vertices,
- green edges,
- blue faces,
- orange cubes.
Example (dimension 1). We should start with dimension $N=1$ though:
Here the cells are:
- a vertex, or a $0$-cell, is $\{n\}$ with $n=...-2,-1,0,1,2,3, ...$;
- an edge, or a $1$-cell, is $[n, n + 1]$ with $n=...-2,-1,0,1,2,3, ...$. $\\$
And,
- $1$-cells are attached to each other along $0$-cells. $\square$
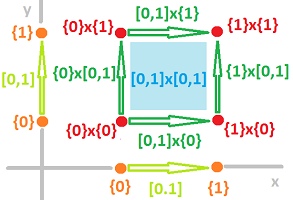
Example (dimension 2). Meanwhile, for the dimension $N=2$ grid, we define (closed) cubical cells for all integers $n,m$ as products:
- a vertex, or a $0$-cell, is $\{n\} \times \{m\}$;
- an edge, or a $1$-cell, is $\{n \} \times [m, m + 1]$ or $[n, n + 1] \times \{m \}$;
- a square, or a $2$-cell, is $[n, n + 1] \times [m, m + 1]$. $\\$
And,
- $2$-cells are attached to each other along $1$-cells and, still,
- $1$-cells are attached to each other along $0$-cells. $\square$
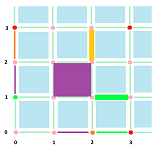
Example.
Cells shown above are:
- $0$-cell $\{3\}\times \{3\}$;
- $1$-cells $[2,3]\times\{1\}$ and $\{2\}\times [2,3]$;
- $2$-cell $[1,2]\times [1,2]$. $\square$
Exercise. Show that intersections of the elements of the basis of the Euclidean space ${\bf R}^N$ with an open cell form its basis. What about the closed cells?
Example (dimension 3). For all integers $n,m,k$, we have:
- a vertex, or a $0$-cell, is $\{n\} \times \{m\}\times \{k\}$;
- an edge, or a $1$-cell, is $\{n \} \times [m, m + 1]\times \{k\}$ etc.;
- a square, or a $2$-cell, is $[n, n + 1] \times [m, m + 1]\times \{k\}$ etc.;
- a cube, or a $3$-cell, is $[n, n + 1] \times [m, m + 1]\times [k, k + 1]$.
$\square$
What we see here is the $N$-dimensional Euclidean space decomposed into $0$-, $1$-, ..., $N$-cells in such a way that
- $N$-cells are attached to each other along $(N-1)$-cells,
- $(N-1)$-cells are attached to each other along $(N-2)$-cells,
- ...
- $1$-cells are attached to each other along $0$-cells.
Definition. In the $N$-dimensional unit grid, ${\bf Z}^N$, a cube is the subset of ${\bf R}^N$ given by the product with $N$ components: $$P:=I_1\times ... \times I_N,$$ such that its $k$th component is either
- an edge $I_k=[m_k,m_k+1],$ or
- a vertex $I_k=\{m_k\},$ $\\$
in the $k$th coordinate axis of the grid. The cube is $n$-dimensional, $\dim P=n$, and is also called a (cubical) cell of dimension $n$, or an $n$-cell, when there are $n$ edges and $N-n$ vertices on this list.
Notation: The set of all unit cubes (of all dimensions) in ${\bf R}^N$ will be denoted by ${\mathbb R}^N$.
Exercise. Show that any $(k - 1)$-dimensional face of a $(k+1)$-dimensional cube $P$ is a common face of exactly two $k$-dimensional faces of $P$.
Exercise. For $k \le 6$, determine the number of vertices and the number of edges of a $k$-cube.
Exercise. Count the faces of a $4$-cube.
A face of $P$ is also a cube given by the same product as $P$ but with some of the edges replaced with vertices.
The boundary cells, also known as $(m-1)$-faces, of an $m$-cell $P$ are certain $(m-1)$-cells that can be computed from the above representation. For each edge $A_i = [n_i, n_i + 1]$ in the product, we define a pair of opposite faces of $P$: $$\begin{array}{lll} P_i^- &:= B_1 \times B_2 \times B_3 \times ... \times B_N,\\ P_i^+ &:= C_1 \times C_2 \times C_3 \times ... \times C_N, \end{array}$$ where
- $B_k=C_k=A_k$ for $k \ne i$,
- $B_i=\{n_i\}$, and
- $C_i=\{n_i+1\}$. $\\$
Then the list of faces of $P$ is $$\{P_i^-,P_i^+:\ A_i = [n_i, n_i + 1],\ i=1,2, ...,N \}.$$ It follows that the total number of $(m-1)$-faces is $2m$.
One can define $k$-faces, $k<m$, of $P$ inductively, as faces of faces.
Exercise. Give a direct construction of (a) $(m-1)$-faces of $m$-cube $P$, (b) all $k$-faces for $k<m$ of $P$. (c) How many of each dimension?
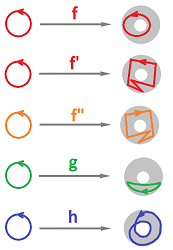
Boundaries of cubical cells
Before we start with the topological analysis of subsets of the Euclidean space made of cubes, let's review what we have learned previously. Starting with the $0$- and $1$-cells of our grid, we are in the exact same situation: the boundary of an edge is still the sum of its endpoints:
The algebraic tool we used was the boundary operator: $$\partial (AB)=A+B.$$ The main lesson of our study of the topology of graphs is:
i.e., formal sums of cells. More precisely,
Example. Let's show what this theory looks like in our new, cubical notation. It is simple in ${\mathbb R}^1$: $$\partial\Big([n,n+1] \Big)=\{n\}+\{n+1\}.$$ And it looks similar for ${\mathbb R}^2$: $$\begin{array}{lllll} &\partial\Big([n,n+1]\times \{k\}\Big) &=\Big(\{n\}+\{n+1\}\Big)\times \{k\}\\ \hspace{.19cm}&&=\{n\}\times \{k\}+\{n+1\}\times \{k\}.&\hspace{.19cm}\square \end{array}$$
Further, our approach is uniform throughout all dimensions:
- The boundary of an edge, $1$-cell, consists of its two endpoints, $0$-cells;
- The boundary a square, $2$-cell, consists of its four edges, $1$-cells;
- The boundary of a cube, $3$-cell, consists of its six faces, $2$-cells;
- etc.
Example. Let's compute the boundaries of the cells from last subsection (${\mathbb R}^2$):
- $0$-cell $\{3\}\times \{3\}$;
- $1$-cells $[2,3]\times\{1\}$ and $\{2\}\times [2,3]$;
- $2$-cell $[1,2]\times [1,2]$.
The boundary of a vertex is empty. Algebraically, $$\partial \{(3, 3) \} = 0.$$
The boundary of an edge is a combination of its endpoints, or algebraically, $$\begin{array}{lll} \partial \Big([2,3] \times \{1 \}\Big) &= \{(2,1) \} + \{(3,1) \},\\ \partial \Big(\{2 \} \times [2,3]\Big) &= \{(2,2) \} + \{(2,3) \}. \end{array}$$
Finally, the square: $$\partial \Big([1,2] \times [1,2]\Big) = [1,2] \times \{1 \} + \{1 \} \times [1,2] + [1,2] \times \{1 \} + \{2 \} \times [1,2].$$ To confirm that this makes sense, let's factor and rearrange the terms: $$\begin{array}{lll} = [1,2] \times \Big( \{1 \} + \{2 \} \Big) & + \Big( \{1 \} + \{2 \} \Big) \times [1,2] \\ = [1,2] \times \partial [1,2] & + \partial [1,2] \times [1,2]. \end{array}$$ We have linked the boundary of the product to the boundaries of its factors! $\square$
The last result may be stated as a formula: $$\partial (a \times b) = a \times \partial b + \partial a \times b.$$ It looks very much like the Product Rule for derivatives, except this time the order of factors matters.
Binary chains and their boundaries
Now, what about boundaries of more complex objects?
They are still made of cells and we simply think of them as formal sums of cells. Just in the case of graphs, we will call them chains. Since boundaries of chains of all dimensions can be empty, we adopt the convention that
Further, we need to combine their boundaries somehow to form the boundary of the object.
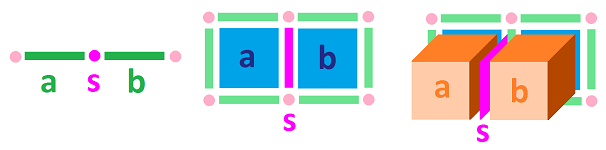
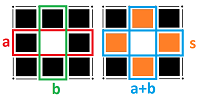
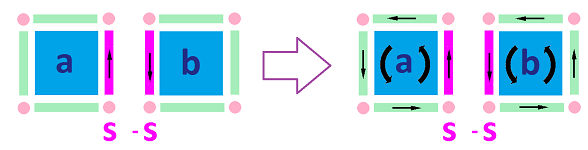
Take a look at these examples of chains that consist of two adjacent $k$-cells, $a$ and $b$, for $k=1,2,3$:
The two $k$-cells share a common face, a $(k-1)$-cell, $s$ (in the middle). This cell is special. In the combined boundary of the chain,
- it appears twice, but
- it shouldn't appear at all! $\\$
Our conclusion is that, for computing the boundary, this algebraic rule of cancellation should apply: $$2x = 0.$$ In other words, if a cell appears twice, it is canceled. The computation is carried out as if we do algebra with binary arithmetic. That's why we can think of our chains both as finite “combinations” and finite binary sums of cells. The latter idea is preferable: $$a = \displaystyle\sum_i s_i \sigma_i,\ s_i \in {\bf Z}_2 .$$ Then, as the boundary operator is defined on each of the cells, we can now extend this definition to all $k$-chains: $$\partial_k(a) := \displaystyle\sum_i s_i \partial_k( \sigma_i ),$$ subject to the cancellation rule.
Let's test this idea with examples.
Example. A formal computation of the boundary of the chain representing two adjacent edges is below: $$\begin{array}{llllll} \partial \Big( \{n \} \times [m, m + 1] + [n, n + 1] \times \{m \} \Big) &= \partial \Big( \{n \} \times [m, m + 1] \Big) + \partial \Big([n, n + 1] \times \{m \} \Big) \\ &= \{(n, m) \} + \{(n, m + 1) \} + \{(n, m) \} + \{(n + 1, m) \} \\ &= \{(n, m + 1) \} + \{(n + 1, m) \}. \hspace{.21cm}\square \end{array} $$
We might prefer a less complex notation just to give an idea of what is going on.
Example. Let's compute the boundary of a curve formed by edges:
$$\begin{array}{lllll} \partial (a + b + f + d + c) &= F + A + A + B + B + E + E + D + D + C \\ &\text{...cancellation...} \\ &= F + C. \end{array}$$ Only the endpoints of the curve remain, as expected. $\square$
Exercise. State this conclusion as a theorem and prove it.
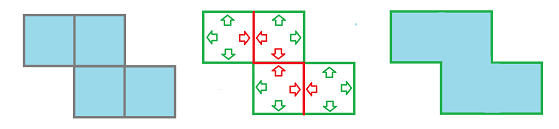
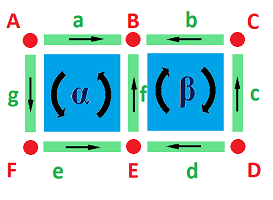
Example. Compute the boundary of the union of two adjacent squares:
$$\begin{array}{cccccc} \partial (\alpha+\beta)&=&\partial\alpha& + & \partial\beta\\ & =&(a+f+e+g)& & +(b+c+d+f)\\ & =&a+e+g &+{\bf (f+f)} & + b+c+d\\ & =&a+e+g &+{\bf 0}& +b+c+d\\ & =&a+b &+c+d & +e+g. \end{array}$$ Only the outside edges appear, as expected. $\square$
In conclusion, the boundary of a region formed by a collection of squares, i.e., a $2$-chain with $N=2$, is made of its “external” edges. Now, each edge is shared by two squares, but
- an “external” edge is shared by one square in the collection and one not in the collection, while
- an “internal” edge is shared by two squares in the collection. $\\$
After application of the boundary operator,
- each “external” edge appears once and stays, while
- each “internal” edge appears twice and cancels:
Exercise. Provide a similar analysis (with sketches) for a collection of edges and a collection of cubes.
What is the relation between cycles and boundaries?
To approach this question, let's try to answer another first:
Dimension $0$. The boundary of a vertex is zero, so the answer is zero.
Dimension $1$. The boundary of an edge is the sum of its two endpoints and the boundaries of those are zero. So the answer is zero again.
Dimension $2$. The boundary of a square is the sum of its four edges. The boundary of each of those is the sum of its two endpoints, or the vertices of the square. Each vertex appears twice and... the answer is zero again.
Example. To confirm this algebraically, we compute the boundary of the boundary of a $2$-cell: $$\begin{array}{lllllll} \partial _1\partial _2 \Big( [n, n + 1] \times [m, m + 1] \Big)\\ = \partial _1 \Big( [n, n + 1] \times \{m \} + \{n \} \times [m, m + 1] + [n, n + 1] \times \{m + 1 \} + \{n + 1 \} \times [m, m + 1] \Big) \\ {\rm ... } \\ = 0.\hspace{.92in}\square \end{array}$$
We can go on.
Dimension $3$. The boundary of a cube is the sum of its six square faces. The boundary of each of those is the sum of its four edges. Since these are the edges of the cube and each appears twice, ... the answer is zero once again:
Exercise. Prove that for the $n$-dimensional case.
So, at least for the cells, the boundary of the boundary is zero. Colloquially,
Are chains just “combinations” of cells?
Consider the following topological problem:
The nature of the problem is topological because the rubber band tends to stretch and shrink on its own and the answer remains the same.
But do we even understand the meaning of “go around”? After all, the band might go back and forth, cancelling some of the wraps. Intuitively, we can allow the band to fully contract and then count... We will sort this out later but, for now, we'll just try to see if we can make any progress with the tools already available.
Mathematically, what we are dealing with is parametric curves:
We are considering maps from a closed interval to the ring (annulus), $f:[0,1]\to A$, with the ends taken to the same point: $f(0)=f(1)$. Then we want to somehow count the number of turns.
At this point, the only available topological tool that seems to match the idea of a parametric curve is the $1$-cycles. Let's try to classify the $1$-cycles in the circle.
In the “hollow square” on the left, it seems clear that
- “the chain $q=a+b+c+d$ goes once around the hole”. $\\$
Let's do this twice. The binary arithmetic then yields unexpected results:
- $p:=q+q=(a+b+c+d)+(a+b+c+d)=0$, even though it seems that “the chain $p$ goes twice around the hole”.
Exercise. Verify the following:
- if “the chain $r$ goes thrice around the hole”, then $r=p$;
- if “the chain $s$ goes once in the opposite direction”, then $s=p$; ... $\\$
Continue.
Our conclusion is now clear: without a way to record the directions of the edges of a cycle, we can't speak of how many turns it makes!
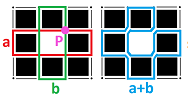
Example. Let's make it clear that the problem isn't that we chose the cycles poorly and their edges got cancelled. In the “thick hollow square” below, we can choose these two $1$-cycles with no overlaps:
With the algebra we have learned, we can easily conclude the following about these cycles:
- $a\not\sim 0$ as $a$ isn't a boundary, and
- $b\not\sim 0$ as $b$ isn't a boundary, but
- $c=a+b\sim 0$ as $c=a+b$ is the boundary of the $2$-chain $s$. $\\$
Again, we are unable to classify the cycles according to the number of times they go around the hole.
To see this example from another angle, we can think of the curve $c=a+b$ as the curve $a$ followed by the curve $b$. In that sense, the curve $c$ circles the hole twice. But with directionless edges, we can also think of $c=a+b$ as a sequence of edges that form a curve that doesn't complete the full circle:
$\square$
To address this problem, we need to learn to count directed edges -- even at the expense of added complexity. We will rebuild the algebra of chains and boundaries for directed edges and, furthermore, “oriented” cells. It appears that all we need to do in order to be able to count turns is to assign a direction to each edge of our cubical grid. Fortunately, they are already chosen for us; they are the directions of the axes:
Nonetheless, we should be able to choose any other combination of directions and our evaluation of the topology of a given cubical complex should remain the same.
No matter how it is done, this step -- by design -- has dramatic implications. We notice that $$AB \ne BA!$$ In fact, $$AB=-BA.$$ It follows that $AB+AB \ne 0$, which forces us to discard the cancellation rule we have replied on: $x+x=0$. By doing so we are abandoning the binary arithmetic itself.
This time, chains are still “combinations of cells” but now these cells can, without cancelling, accumulate: $x+x=2x$, etc. In fact, one can think informally of chain $2x$ as if cell $x$ is visited twice. These are the interpretations of the new, directed chains:
- chain $x$ visits cell $x$ once going in the positive direction (that of the axis);
- chain $2x$ visits cell $x$ twice;
- chain $3x$ visits cell $x$ thrice;
- chain $-x$ visits cell $x$ once going in the negative direction;
- chain $0=0x$ doesn't visit cell $x$ (or any other);
- chain $x+2y+5z$ visits cell $x$ once, cell $y$ twice, and cell $z$ five times -- in no particular order.
Definition. A $k$-chain in a cubical complex $K$ is a “formal linear combination of $k$-cells” in the complex: $$S=r_1a_1+r_2a_2+...+r_na_n,$$ where $a_1,a_2, ...,a_n$ are $k$-cells in $K$ and the coefficients $r_1,r_2, ...,r_n$ are some scalars.
These “scalars” are chosen from some collection $R$. What kind of set is $R$? First, we need to be able to add chains, $$\begin{array}{lll} (r_1a_1+r_2a_2+...+r_na_n)+(s_1a_1+s_2a_2+...+s_na_n)\\ \qquad \qquad\qquad\qquad\qquad =(r_1+s_1)a_1+(r_2+s_2)a_2+...+(r_n+s_n)a_n, \end{array}$$ and to multiply chains by scalars, $$\begin{array}{lll} p(r_1a_1+r_2a_2+...+r_na_n)\\ \qquad \qquad\qquad\qquad\qquad =(pr_1)a_1+(pr_2)a_2+...+(pr_n)a_n. \end{array}$$ These requirements make us choose $R$ to be a ring. Clearly, if we choose $R={\bf Z}_2$, we are back to the binary theory, which remains a valid choice.
For simplicity and convenience, we choose to deal with chains with $$\begin{array}{|c|} \hline \\ \quad \text{real coefficients} \quad \\ \\ \hline \end{array}$$ for the rest of this chapter: $R={\bf R}$.
Orientations and boundaries
A crucial part has been the cancellation rule of $R={\bf Z}_2$. With this rule, all cells that appear twice in a given chain, such as the boundary of a cell, cancel. Without this rule, it will no longer automatically happen!
The idea is then to assume that -- before any computations start -- an “orientation” is assigned to each cell in $K$. Then each cell $s$ may appear in computations with either positive, as $s$, or negative orientation, as $-s$. This should be done in such a way that, when computing the boundary of a chain $a+b$ with two adjacent cells $a,b$ present, each “internal face” $s$ (shared by $a$ and $b$) will appear twice, but with the opposite orientations and, therefore, cancel: $s+(-s)=0$.
But what is an orientation?
We already know the answer for $1$-cells. The orientation means a choice of the direction of the edge and this is how they are supposed to cancel:
To have them cancel, let's choose the orientation for either of the $2$-cells involved to mean the choice of the counterclockwise direction around it. Then clockwise direction will be the opposite orientation. Next, the orientations of the boundary $1$-cells of this $2$-cell are “read” by going around this cell. Then, indeed, there will be $s$ coming from the boundary of the first cell and $-s$ from the boundary of the second.
What about $0$-cells? The idea of an orientation of a point might seem strange. Instead, let's ask again, how do these cells cancel?
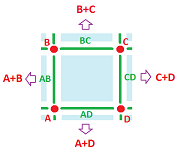
The boundary of a $1$-cell $AB$ is, as before, a linear combination of its two endpoints $A$ and $B$, but what are the coefficients? What helps here is that we also expect the boundary of $AB+BC$ to be a linear combination of $A$ and $C$, so $B$ has to cancel: $$\begin{array}{lll} ?A+?C&=\partial (AB+BC)&=\partial (AB)+\partial (BC)\\ &=(?A+?B)+(?B+?C)&=?A+(?B+?B)+?C. \end{array}$$ Therefore, $B$ has to appear with the opposite signs! It might appear with “$+$” in $\partial (AB)$ and with “$-$” in $\partial (BC)$. But the only difference between them is the position of $B$ with respect to the direction of these edges, the beginning or the end. We choose then the boundary of an edge to be equal to its final point minus the initial point: $$\partial (a) = \partial (AB) := B-A.$$ Then the orientation of a $0$-cell works as expected even though it doesn't have a visible meaning. (It seems that the orientation means what the algebra says it means!)
No doubt, the boundaries of $0$-chains are all, as before, equal to $0$; $$\partial (A) := 0.$$
Example. Let's confirm that the definition works. We assigned random orientations to $1$- and $2$-cells:
Then, $$\partial (a-b) = \partial a - \partial b =(A-B)-(B-C)=A-C,$$ and the interior vertex $B$ is cancelled. And so it is for the chain $b-a$, but not for $a+b$.
Next, $$\partial (\alpha-\beta) = \partial \alpha- \partial \beta =(-a+f+e+g)-(-b-c+d+f)=-a+b+c-d+e+g,$$ and the interior edge $f$ is cancelled. And so it is for the chain $\beta - \alpha$, but not for $\alpha+\beta$. $\square$
Exercise. Find three linearly independent $1$-cycles in the last example and compute their boundaries.
We are now to reconstruct the homology theory for the new setting.
Proposition. For any cubical complex $K$ (and any choice of orientations of its cells), the composition of boundary operators $$\partial _1\partial _2:C_2(K)\to C_0(K)$$ is zero.
Exercise. Represent the sets below as realizations of cubical complexes. For each of them:
- (a) find the chain groups and find the boundary operator as a matrix;
- (b) using only part (a) and linear algebra, find $Z_k,B_k$ for all $k$, including the generators;
- (c) repeat the computations for two more choices of coefficients, $R={\bf Z},{\bf Z}_3$.
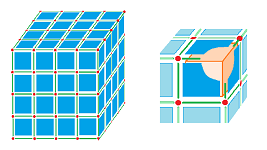
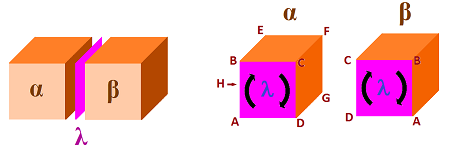
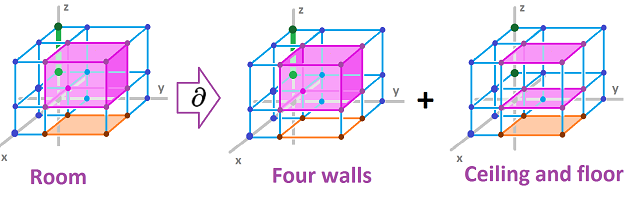
The $3$-dimensional case is more complex. Even though we understand the meaning of the orientation of these $2$-cells, what can we way about these two adjacent $3$-cells $\alpha$ and $\beta$?
We need to define orientation for them in such a way that the $2$-cell $\lambda$ would appear with two opposite orientations -- as a boundary face of $\alpha$ and $\beta$. How? Notice that understanding orientation as an order of its vertices works for $1$-cells, say, $a=AB$, and for $2$-cells, say, $\tau =ABCD$. So, maybe it's a good idea to try the same for the $3$-cells, say, $\alpha = ABCDEFG$?
Exercise. Show that such a definition won't produce what we expect. Hint: does it really work for dimension $2$?
Defining orientation for the case of higher dimensions will require using the product structure of the space.
Computing boundaries with a spreadsheet
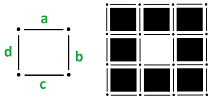
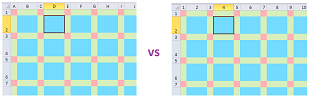
Cells on the plane can be presented in a spreadsheet such as Excel. Below, some of the rows and columns are narrowed in order to emphasize the $1$-dimensional nature of the edges and the $0$-dimensional nature of the vertices:
The cells are represented:
- left: in the standard style, and
- right: in the $\texttt{R1C1}$ reference style.
The highlighted cell is given by
- $\texttt{D2}$, and
- $\texttt{R2C4}$, $\\$
respectively. The latter is clearly more mathematical and that's the one we will use. Notice, however, that the coordinate axes go down and right as in a matrix, instead of right and up as we are used to in the Cartesian system.
Also, the coordinates differ from those in the above discussion by a factor of two: the highlighted cell is located at $(1,2)$. Then
- $0$-cells are $(odd,odd)$,
- $1$-cells are $(odd,even)$ and $(even,odd)$,
- $2$-cells are $(even,even)$.
The chains are encoded by putting $0$s and $1$s in all cells. In the former case, the cell is white and the number is invisible while in the latter case, the cell is colored according to its dimension.
Next, we implement the boundary operator.
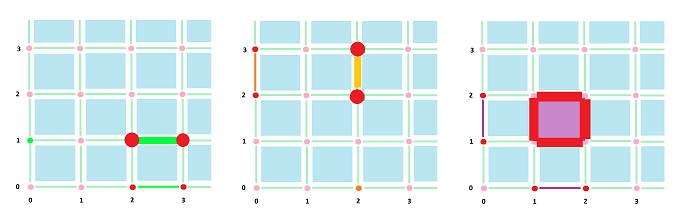
These are the results of computing boundaries, for a $1$-chain (green):
and a $2$-chain (blue):
The approach to the algorithm for computing the boundary operator is very different from the algebra we have done. Compare the following.
- Normally, to compute the boundary of a $k$-chain, we evaluate the boundary of each of its $k$-cells as the sum of this cell's boundary cells (dimension $k-1$), add them, and then cancel the repetitions.
- Now, we look at each $(k-1)$-cell present in the spreadsheet, add the values of the $k$-cells of the chain adjacent to it, and then find out whether the result makes this cell a part of the boundary of the chain. $\\$
The results are of course the same.
The code is very simple.
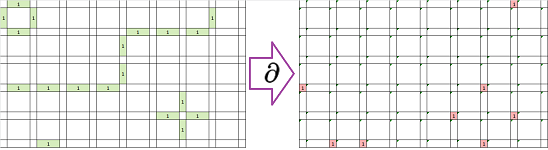
Dimension $0$: For each vertex, we compute the sum, modulo $2$, of the values at the four edges adjacent to it: $$\texttt{ = MOD( RC[-21] + R[-1]C[-20] + RC[-19] + R[1]C[-20], 2)}$$ Then the result is placed on the right. It follows that,
- if the curve isn't there, we have $0+0+0+0=0$;
- if the curve is passing by once, we have $1+0+1+0=0$;
- if the curve is passing by twice, we have $1+1+1+1=0$;
- if the curve ends here, we have $1+0+0+0=1$.
Dimension $1$: For each edge, we, similarly, compute the sum of the values at the two adjacent faces; horizontal: $$\texttt{ = MOD( R[-1]C[-20] + R[1]C[-20], 2)}$$ and vertical: $$\texttt{ = MOD( RC[-21] + RC[-19], 2)}$$ Then,
- if the edge is away from the region, we have $0+0=0$;
- if the edge is inside the region, we have $1+1=0$;
- if the edge is on the boundary of the region, we have $1+0=1$.
Exercise. Devise and implement a similar algorithm for $3$-chains. Hint: use the “sheets” as layers.
This is how these simple formulas for dimension $1$ are implemented with a spreadsheet program such as Excel:
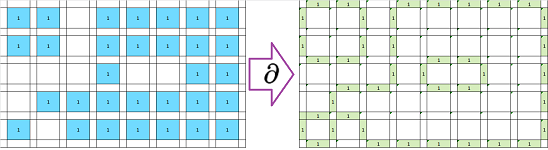
Example. As an illustration, this is a $2$-chain (blue) and its boundary, a $1$-chain (green), computed and presented in a spreadsheet:
The direction of an edge is given by $1$ if it goes along the axis and $-1$ if it goes against it. Observe how the directions change as the boundary curve goes counterclockwise. $\square$
Exercise. What happens to the values of the boundary chain if we replace all $1$'s in the $2$-chain on the left with $2$'s? What happens to the shape of the boundary if we make them random?
The method is identical to that for the binary case.
Dimension $0$: For each vertex, we compute the sum of the values at the four adjacent edges with appropriate signs: $$\texttt{ = -s!RC[-1] + s!RC[1] - s!R[-1]C + s!R[1]C}$$ where $s$ refers to the worksheet that contains the chain. Then,
- if the curve isn't there, we have $0+0+0+0=0$;
- if the curve is passing by once, we have $1+0-1+0=0$ (in some order);
- if the curve is passing by twice, we have $1-1+1-1=0$;
- if the curve begins or ends here, we have $1+0+0+0=1$ or $-1$.
Dimension $1$: For each edge, we, similarly, compute the sum of the values at the two adjacent faces with appropriate signs, horizontal: $$\texttt{ = s!R[-1]C - s!R[1]C}$$ vertical: $$\texttt{ = -s!RC[-1] + s!RC[1]}$$ Then,
- if the edge is away from the region, we have $0+0=0$;
- if the edge is inside the region, we have $1-1=0$;
- if the edge is on the boundary of the region, we have $1+0=1$.
Exercise. Modify the code to compute boundaries over ${\bf Z}_p$.
Example. We can compute boundaries of more complex chains:
We demonstrated here that the result of two boundary operators applied consecutively is, again, $0$. $\square$
Exercise. Define the group $C$ of all chains (as opposed to the collection of all groups $C_k$ of $k$-chains, $k=0,1, ...$). Define the boundary operator for $C$. Hint: consider the picture above.
The boundary of a cube in the $N$-dimensional space
In the presence of the product structure, the decision about orientations can be made for us and in a uniform fashion: all edges are directed along the coordinate axes. For $1$-cells in the plane, the formulas are: $$\begin{array}{lll} \partial \big(\{0 \} \times [0,1]\big) &= -\{(0,0) \} + \{(0,1) \},\\ \partial \big([0,1] \times \{0 \}\big) &= -\{(0,0) \} + \{(1,0) \}. \end{array}$$
For a $2$-cell, its boundary should, as we know, be the four oriented edges appearing as we go counterclockwise around the square:
Then, $$\begin{array}{lllll} &\partial \big([0,1] \times [0,1]\big) \\ &= [0,1] \times \{0 \} + \{1 \} \times [0,1] - [0,1] \times \{1 \} - \{0 \} \times [0,1]. \end{array}$$ Here the edges are always oriented along the axes and going counterclockwise around the square produces these signs. To confirm that this makes sense, let's factor and rearrange the terms: $$\begin{array}{llll} & = & [0,1] \times \big( \{0 \} - \{1 \} \big) & + \big( \{1 \} - \{0 \} \big) \times [0,1] \\ & = & - [0,1] \times \partial [0,1] & + \partial [0,1] \times [0,1]. \end{array}$$ That's how products behave under the boundary operator.
Warning: A common mistake in elementary calculus is to assume that the derivative of the product is the product of the derivatives. Don't make a similar mistake and assume that the boundary of the product is the product of the boundaries! Consider: $$\partial (a\times b) \ne \partial a \times \partial b.$$ Then, the left-hand side is the four edges of the square and the right-hand side is its four vertices. Even the dimensions/units don't match!
The correct formula of the product rule for boundaries is: $$\partial (a\times b)=\partial a \times b +(-1)^{\dim a} a \times \partial b,$$ for cells and chains of all dimensions.
Exercise. Use to the formula to compute the boundary of a cube $\partial\big( [0,1]\times[0,1]\times[0,1] \big)$ and confirm that the opposite faces appear with opposite orientations.
We will rely on the product structure to compute the boundary of the $k$-dimensional cube in the $N$-dimensional space.
Recall that a $k$-cube is the product of $k$ edges and some vertices. In ${\mathbb R}^N$, a cubical $k$-cell can be represented as the product if the $N$-dimensional space is seen as the product of $N$ copies of ${\bf R}$: $$\begin{array}{cccccccccccccccc} Q^k&=\displaystyle\prod_{i=1}^N A_i&= &A_1&\times &... &\times &A_{s-1}& \times &A_s &\times &A_{s+1}&\times &...& \times &A_N\\ \cap & \cap &&\cap & &&&\cap &&\cap &&\cap &&&&\cap \\ {\bf R}^N&=\displaystyle\prod_{i=1}^N {\bf R}^1&=& {\bf R}&\times& ... &\times &{\bf R}& \times &{\bf R}& \times &{\bf R}&\times &... &\times &{\bf R}. \end{array}$$ Here, each $A_i$ is a subset of the $i$th axis, a copy of ${\bf R}$, which is either
- an edge, such as $[m,m+1]$, or
- a vertex, such as $\{m\}$. $\\$
There are exactly $k$ edges on the list. Note that this representation is unique.
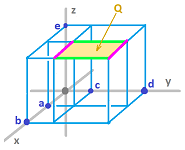
Example. Here's an example of a $2$-cube, a square, in the $3$-dimensional space: $$Q^2=[a,b]\times [c,d] \times \{e\},$$ illustrated below:
$\square$
Even though the meaning of the boundary as shown above is clear, we proceed to give a general definition.
We already understand products of cubes. If
- $A^p$ is an $p$-cube in ${\mathbb R}^n,$
- $B^q$ is an $q$-cube in ${\mathbb R}^m,$ then
- $A^q\times B^p$ is an $(p+q)$-cube in ${\mathbb R}^{n+m}$. $\\$
We also need to understand products of chains. If
- $a \in C_p({\mathbb R}^n)$,
- $b \in C_q({\mathbb R}^m)$, then
- $a\times b \in C_{p+q}({\mathbb R}^{n+m})$. $\\$
Predictably, this product is defined via summation of the pairwise products of the cubes. If
- $a = \sum_i a_i P_i$, and
- $b = \sum_i b_i Q_i$,
where $a_i,b_i$ are the scalars and $P_i,Q_i$ are the cells (finitely many!), then
- $a\times b := \sum_i a_ib_i (P_i\times Q_i)$. $\\$
Definition. The definition of the boundary is inductive.
As the base of induction, we define the boundary for $1$-cells, the edges. Suppose $$Q^1:=\displaystyle\prod_{i=1}^N A_i,$$ with
- $A_s:=[m_s,m_s+1]$ and
- $A_i:=\{m_i\}$ for $i \ne s$, $\\$
for some particular choice of $s$. Its boundary is also a product: $$\partial Q^1=\displaystyle\prod_{i=1}^N B_i.$$ What are the values of these components? We define, as before, the boundary with a change in a single component:
- $B_s=\partial A_s=\{m_s+1\} - \{m_s\}$ and
- $B_i=A_i=\{m_i\}$ for $i \ne s$.
We rephrase the formula: $$\begin{array}{ll} \partial \Big( \{m_1\}\times... \times \{m_{s-1}\}\times [m_s,m_s+1]\times \{m_{s+1}\}\times ... \times \{m_N\} \Big)\\ = \{m_1\}\times... \times \{m_{s-1}\}\times \big(\{m_s+1\}-\{m_s\}\big) \times \{m_{s+1}\}\times ... \times \{m_N\}. \end{array}$$ This is, as expected, the endpoint $$\{m_1\}\times... \times \{m_{s-1}\}\times \{m_s+1\} \times \{m_{s+1}\}\times ... \times \{m_N\}$$ minus the beginning point of the edge: $$\{m_1\}\times... \times \{m_{s-1}\}\times \{m_s\} \times \{m_{s+1}\}\times ... \times \{m_N\}.$$
Thus, we have defined the boundary for all edges in the $N$-dimensional space for all $N$. We also know the boundary of any vertex: $\partial V:=0$.
Next we assume that the boundary is defined for all $k$-cells -- in the $N$-dimensional space for all $N$ -- and then extend the definition to $(k+1)$-cells, as follows. We simply use the fact that any $(k+1)$-cell $Q^{k+1}$ is the product of a $k$-cell $Q^k$ with an edge $E$: $$Q^{k+1}=Q^k\times E.$$
More precisely, we deal with these cells in these Euclidean spaces:
- $Q^k\subset {\bf R}^n$ is a $k$-cube, and
- $A=E\subset {\bf R}^1$ is an edge, or
- $A=V\subset {\bf R}^1$ is a vertex, then
- $Q^k\times A \subset {\bf R}^n \times {\bf R}^1$ is a $k$- or a $(k+1)$-cube.
Finally, the boundary of a cubical cell $Q^{k+1}=Q^k\times A$ constructed this way is defined in terms of its components.
- Case 1: if $A$ is an edge $E$, then
$$\partial (Q^k\times E):=\partial Q^k \times E +(-1)^k Q^k \times \partial E.$$
- Case 2: if $A$ is a vertex $V$, then
$$\partial (Q^k\times V):=\partial Q^k \times V. $$ $\square $
Plainly, both cases are just manifestations of the more general product rule (as $\partial V=0$).
Using this definition, we can compute the boundary of any cubical cell: $$A_1\times ... \times A_{s-1} \times A_s \times A_{s+1}\times ... A_n$$ by adding one component $A_s$ at a time and, depending on whether this is an edge or a vertex, and use one of the two formulas given above:
- $A_1$,
- $A_1\times A_2$,
- $A_1\times A_3\times A_3$,
- ...
- $A_1\times ... \times A_{s-1} \times A_s$,
- ...
- $A_1\times ... \times A_{s-1} \times A_s \times A_{s+1}\times ... \times A_n$.
Example. Let's find the boundary of $$Q^2:=[0,1]\times \{5\} \times [3,4].$$ Here
- $A_1:=[0,1]$,
- $A_2:=\{5\}$,
- $A_3:=[3,4]$. $\\$
Starting from the left. For $\partial A_1$: $$\partial \big( [0,1] \big)=\{1\}-\{0\}.$$ Next for $\partial (A_1\times A_2)$. From the definition, as the second component is a vertex, it's case 2. We substitute the last equation: $$\partial \big([0,1]\times\{5\}\big)=\partial [0,1]\times\{5\} =\big(\{1\}-\{0\}\big)\times \{5\}.$$ Now for $\partial (A_1\times A_2\times A_3)$. The last component is an edge, so it's case 1. We substitute the last equation: $$\begin{array}{lll} \partial \Big( ([0,1]\times\{5\}) \times [3,4] \Big)\\ =\partial \big([0,1]\times\{5\}\big) \times [3,4] +(-1)^1 \big([0,1]\times\{5\}\big) \times \partial [3,4]\\ =\big(\{1\}-\{0\}\big)\times \{5\}\times [3,4]-\big([0,1]\times\{5\}\big)\times \big(\{4\}-\{3\}\big). \end{array}$$ To check that the answer makes sense, verify these facts: it's in $3$-space; its dimension is $1$; there are $4$ edges; all lie in plane $y=5$, etc. $\square$
Exercise. Illustrate this computation with a picture similar to the one in the beginning of the subsection. From that picture, compute the boundary of square $Q$ and of the whole cube.
The chain complex of ${\mathbb R}^N$
Suppose the ambient dimension $N$ is fixed as well as the integer grid ${\bf Z}^N$ of the Euclidean space ${\bf R}^N$.
Notation:
- ${\mathbb R}^N$ is the set of all cells (of all dimensions) in the grid,
- $C_k(L)$ is the set of all $k$-chains in a given collection $L\subset {\mathbb R}^N$ of cells, and, in particular,
- $C_k:=C_k({\mathbb R}^N)$ is the set of all $k$-chains in ${\mathbb R}^N$. $\\$
We will call $C_k(L)$ the $k$th chain group of $L$.
We extend the boundary operator from the one defined for the cells only to one defined for all chains. We say that “we use linearity” and this is what we mean: as every $k$-chain is a formal linear combination of $k$-cells, the $k$-cells form the basis of the space of $k$-chains $C_k$. The idea is familiar from linear algebra:
- a linear operator is fully defined by its values on the basis elements; and
- any choice of the values on the basis determines a linear operator. $\\$
The latter is exactly what we have. Indeed, $\partial _k$ is defined on the $k$-cells and now these values are combined to produce the values for all $k$-chains: $$\partial _k \Big(\displaystyle\sum_i r_i p_i \Big) = \displaystyle\sum_i r_i \partial _k p_i ,$$ where $p_i$ are the $k$-cells (finitely many) and $r_i$ are the real scalars.
Definition. Given a $k$-chain $s\in C_k$, $$s = a_1 + a_2 + ... + a_n,$$ where $a_1, a_2, ..., a_n$ are $k$-cells, the boundary $\partial s$ of $s$ is given by $$\partial s := \partial a_1 + \partial a_2 + ... + \partial a_n.$$
So, the boundaries of $k$-cells are $(k-1)$-chains, and, moreover, the boundaries of $k$-chains are $(k-1)$-chains as well. Then, boundaries are found by a well-defined function $$\partial =\partial _k: C_{k} \to C_{k-1}.$$ It is called the $k$th boundary operator.
Just as we did before, we notice that this function is simply an extension of a function defined on the generators of a group to the rest of the group -- by additivity. Therefore, we have the following.
Theorem. The boundary operator is a homomorphism.
We now present the big picture of the algebra of chains and their boundaries.
The homomorphisms $\partial _k : C_{k} \to C_{k-1},\ k=1,2, ...$, if written consecutively, form a sequence: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} C_N & \ra{\partial_N} & C_{N-1} & \ra{\partial_{N-1}} & ... & \ra{\partial_{k+2}} & C_{k+1} & \ra{\partial_{k+1}} & C_{k} & \ra{\partial_k} & ... & \ra{\partial_1} & C_0. \end{array}$$ As always, consecutive arrows are understood as compositions. We would like to treat these groups uniformly and we append this sequence with two more items, one in the beginning and one at the end. Both are zero groups: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} 0&\ra{\partial_{N+1}}&...&... &... &... &\ra{\partial_0}&0. \end{array}$$ The two groups are attached to the rest of the sequence with homomorphisms that are, of course, zero. The result is this sequence of groups and homomorphisms called the chain complex of ${\mathbb R}^N$: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} 0&\ra{\partial_{N+1}=0}&C_N&\ra{\partial_N}&...&\ra{\partial_{k+1}}&C_{k}&\ra{\partial_k}&...&\ra{\partial_1}&C_0&\ra{\partial_0=0}&0. \end{array}$$
The boundary of a boundary is zero
From the definition of the boundary, we have the following:
Proposition. Suppose:
- $Q^k\subset {\bf R}^n$ is a $k$-chain, and
- $A\subset {\bf R}^1$ is $0$- or $1$-chain, and
- $Q^k\times A \subset {\bf R}^n \times {\bf R}^1$ is a $k$- or a $(k+1)$-chain. $\\$
Then $$\partial (Q^k\times A)= \partial Q^k \times A +(-1)^k Q^k \times \partial A.$$
Exercise. Prove the proposition.
The formula is illustrated below for $k=2$. The cube as the product of a square and an edge is on the left and the two terms of the formula are shown on the right:
An even more general result is below:
Theorem (Product Formula for Boundaries). Suppose
- $a \in C_i({\mathbb R}^n)$,
- $b \in C_j({\mathbb R}^m)$, and
- $a\times b \in C_{i+j}({\mathbb R}^{n+m})$. $\\$
Then $$\partial (a\times b)=\partial a \times b +(-1)^{i} a \times \partial b.$$
Theorem (Double Boundary Identity). For oriented chains of cubical complexes, $$\partial\partial =0.$$
Proof. The proof is based on the same induction as the definition itself.
The inductive assumption is that in any $N$-dimensional space $$\partial\partial Q^i=0$$ for all cubical $i$-cells, for all $N$, for all $k\le N$, and all $i=0,1, ...,k$.
Now we represent a $(k+1)$-cube as the product of a $k$-cube and an edge as the last component: $$Q^{k+1}=Q^k\times E.$$ Now we just compute what we want. From the definition: $$\partial Q^{k+1}=\partial ( Q^{k}\times E)=\partial Q^k \times E +(-1)^k Q^k \times \partial E.$$ Next, $$\begin{array}{llllllll} &\partial \partial Q^{k+1} & = \partial\Big( \partial Q^k \times E + (-1)^k Q^k \times \partial E\Big) & \text{ and by linearity of } \partial ...\\ && =\partial\Big( \partial Q^k \times E\Big) + (-1)^k \partial\Big(Q^k \times \partial E\Big) & \text{ now use the last proposition, twice...}\\ && =\partial\partial Q^k \times E +(-1)^{k-1}\partial Q^k \times \partial E \\ && +(-1)^k \Big( \partial Q^k \times \partial E +(-1)^k Q^k\times \partial\partial E\Big) & \text{ now use the assumption...} \\ && =0 \times E +(-1)^{k-1}\partial Q^k \times \partial E\\ && +(-1)^k \Big( \partial Q^k \times \partial E +(-1)^k Q^k\times 0\Big)\\ && =(-1)^{k-1}\partial Q^k \times \partial E+(-1)^k \partial Q^k \times \partial E \\ \hspace{.01in}&& =0.&\hspace{.4in}\blacksquare \end{array}$$
Is it a coincidence that this computation feels like differentiation in elementary calculus?
Exercise. Supply the missing part of the above proof. Hint: the last component of the cube may be a vertex.
Exercise. Derive from the theorem the same formula for the binary arithmetic.
Since the $(k+1)$-cells are the generators of the chain group $C_{k+1}$ and the values of the homomorphism $\partial _k\partial _{k+1}$ are zeroes, it follows that the whole homomorphism is $0$: $$\partial _k\partial _{k+1} \Big(\displaystyle\sum_i s_i\Big)= \displaystyle\sum_i \partial _k\partial _{k+1} (s_i)= \displaystyle\sum_i \ 0=0.$$ The composition is trivial!
Theorem (Double Boundary Identity). The composition of two boundary operators $$\partial _{k}\partial _{k+1}:C_{k+1}\to C_{k-1}$$ is zero.
Definition. Any sequence of groups and homomorphisms: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccccccc} G_N & \ra{f_N} & G_{N-1} & \ra{f_{N-1}} & ... & \ra{f_2} & G_1 & \ra{f_1} & G_0, \end{array}$$ that satisfies $f_kf_{k+1}=0,\ \forall k=1, ...,N-1$, is called a chain complex.
Exercise. Give an example of a chain complex with $f_k \ne 0,\ \forall k=2, ...,N-1$.
The compact form of the above identity is: $$\begin{array}{|c|} \hline \\ \quad \partial \partial = 0 \quad \\ \\ \hline \end{array}$$
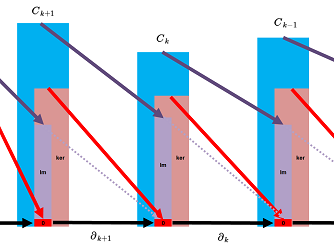
Corollary. $$B_k\subset Z_k,\ \forall k=0,1,2, ...$$ or, $$\operatorname{Im} \partial_{k+1} \subset \ker \partial_k.$$
This condition is commonly illustrated with this informal diagram: