Tangent cone

Cubical (aka "discrete") manifolds are still manifolds, but made up of cells. What are the tangents of cubical complexes?

They aren't differentiable manifolds. Then there should be no tangents at the corners!

So, how do we understand the tangents?

Introduction

A $1$-manifold looks like this:

What happens at $a$? What do we need to do instead for $T_aM$?

Observation: Just a few "bad" points, the rest is OK.

Stand them up.

Glue them together:

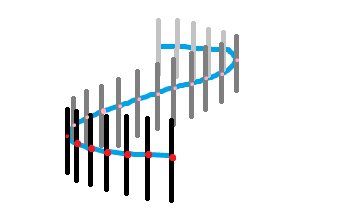
Tangent vectors come from parametrization:

Here the tangent turns $90^o$. That's why $T_aM$ is "thick" here. This idea comes from the smooth case, when we record how the tangents turn, as follows.

How to glue these together?

What about $2$-manifolds? What is $T_aM$ at corners?

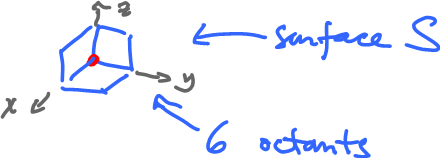
A $2$-manifold is a surface and as a cubical complex it will look like this, compared to a $1$-manifold:

If we are to compute the tangent bundle of this kind of corner, then, algebraically, $T_aS$ should be the closure of the complement of the following: $$\left\{ \begin{array}{} x > 0 \\ y > 0 \\ z > 0 \end{array} \right\} \cup \left\{ \begin{array}{} x < 0 \\ y < 0 \\ z < 0 \end{array} \right\}.$$

Tangent cone

Let $A$ be any subset of $R^n$ and suppose $x \in A$. We define the tangent cone $TC_x(A) $ of $A$ at $x$ as a certain set of vectors: $$TC_x(A) = Cl \left\{v \in {\bf R}^{n}: \lim _{t \rightarrow 0} \frac{d(x + tv,A)}{t}=0 \right\},$$ where $Cl$ stands for the closure.

So, a vector $v$ is considered tangent at a point $x \in A$, if the ray beginning at $x$ and pointing in the direction of $v$ approaches $A$ faster than linearly.

For example, if $A$ is the graph of $y=x\sin 1/x$, then $$TC_0(A)=\{(r,\theta):-\pi / 4 \le \theta \le \pi /4, 3 \pi / 4 \le \theta \le 5 \pi /4\}.$$ For the region below this graph: $$TC_0(A)=\{(r,\theta):3 \pi / 4 \le \theta \le \pi /4\}.$$

Exercise. Compute the tangent cone of the graphs of these functions and that of the regions under these graphs:

• $y= \sin 1/x$,
• $y=x^2 \sin 1/x$,
• $y=\sqrt{x} \sin 1/x$.

Two observations. First, this is a "cone", i.e., $$TC_x(A)={\bf R} \cdot TC_x(A)=\{\alpha v: v \in TC_x(A),\alpha \in {\bf R} \}.$$ Second, the set includes all interior points of $A$.

In the continuous case, the tangent space $T_x(A)$ is a vector space. The reason is that it should be able to accommodate parametric curves in $A$ with the tangents at $x$ of any direction and magnitude. But if we try to "expand" $TC_x(A)$ and taking its span, we will likely produce the whole ${\bf R}^{n}$.

Indeed, let's take the example of the two-edge $C$ curve that goes up to $0$ and then goes right:

Then the tangent cone is the set of all multiples of the basis vectors of the plane (the axes): $$TC_0(C)={\bf R} \cdot \{(1,0)\} \cup {\bf R} \cdot \{(0,1)\}.$$ Therefore, $${\rm span } TC_0(C) = {\bf R}^2 .$$

What about the tangent bundle?

Let's recall that the tangent bundle of a simple curve is homeomorphic to a strip:

Note: In general, tangent bundles are manifolds.

We expect to have the same result for cubical curves.

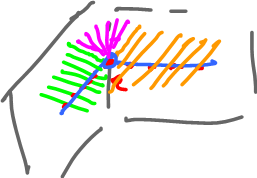
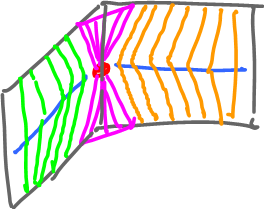
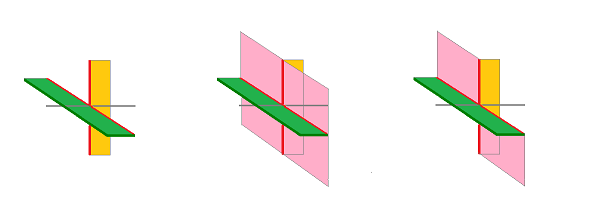
Let's consider the tangent bundle of the two-edge curve above. The tangent bundles of the two edges are strips and we are supposed to use the tangent cone $TC_0(C)$ at the zero to glue together these tangent bundles. And the result should be just a simple strip.

This is not the case. If we use $TC_0(C)$, the result is two strips attached to each other by a point. If we use the ${\rm span } TC_0(C)$ instead, the result is a plane with two strips attached. You can see the problem in the first two images below:

So, whether we use the tangent cone or its span, the tangent bundle created this way isn't homeomorphic to the that of the corresponding smooth curve! Too little in the former case; too much in the latter.

We need to amend our definition of the tangent space in order to have the tangent bundle which is a surface as the one we see in the third image.

We define the tangent space of submanifold $M$ of ${\bf R}^n$ at $x$ as: $$T_xM=\{v-u: v,u \in TC_x(M)\}.$$

Exercise. Prove that for differentiable manifolds, the definitions match.

The definition corresponds to the analysis we started with. Of course in the setting of cubical complexes the things are much simpler that that because we don't have to deal with limits. To understand the structure of the tangent space at cell $a$ we only need to consider the cells that meet at $a$.

The tangent bundle is again the disjoint union of the tangent spaces.

Exercise. Prove that $TC$ is homeomorphic to a strip.