This site is being phased out.
Systems of ODEs
Contents
- 1 The predator-prey model
- 2 Qualitative analysis of the predator-prey model
- 3 Solving the Lotka–Volterra equations
- 4 Vector fields and systems of ODEs
- 5 Discrete systems of ODEs
- 6 Qualitative analysis of systems of ODEs
- 7 The vector notation and linear systems
- 8 Classification of linear systems
- 9 Classification of linear systems, continued
The predator-prey model
This is the IVP we have considered so far: $$\frac{\Delta y}{\Delta t}=f(t,y),\ y(t_0)=y_0,$$ and $$y'=f(t,y),\ y(t_0)=y_0.$$ The equations show how the rate of change of $y$ depends on $t$ and $y$.
What if we have two variable quantities dependent on $t$?
The simplest example is as follows:
- $x$ is the horizontal location, and
- $y$ is the vertical location. $\\$
We have already seen this simplest setting of free fall: $$\begin{cases} \frac{\Delta x}{\Delta t}=v_x,\\ \frac{\Delta y}{\Delta t}=v_y-gt, \end{cases} \text{ and } \begin{cases} x'=v_x,\\ y'=v_y-gt. \end{cases}$$ It is just as simple when arbitrary functions are in the right-hand sides of the equations (the continuous case is solved by integration). Here the rate of change of the location depends on the time $t$ only.
More complex is the situation when the rate of change of the location depends on the location. When the former depends only on its own component of the location, the motion is described by this pair of ODEs: $$\begin{cases} \frac{\Delta x}{\Delta t}=g(x),\\ \frac{\Delta y}{\Delta t}=h(y). \end{cases} \text{ and } \begin{cases} x'=g(x),\\ y'=h(y). \end{cases}$$ The solution consists of two solutions to the two, unrelated, ODEs. We can then apply the methods of Chapter 24.
As an example of quantities that do interact, let's consider the predator-prey model.
Let
- $x$ be the number of rabbits and
- $y$ be the number of foxes in the forest.
Let
- $\Delta t$ be the fixed increment of time.
Even though time $t$ is now discrete, the “number” of rabbits $x$ or foxes $y$ isn't. Those are real numbers in our model. One can think of $.1$ rabbits as if the actual number is unknown but the likelihood that there is one somewhere is $10\%$.
We begin with the rabbits. There are two factors affecting their population.
First, we assume that they have an unlimited food supply and reproduce in a manner described previously -- when there is no predator. In other words, the gain of the rabbit population per unit of time through their natural reproduction is proportional to the size of their current population. Therefore, we have: $$\text{rabbits' gain }=\alpha\cdot x \cdot \Delta t,$$ for some $\alpha>0$.
Second, we assume that the rate of predation upon the rabbits to be proportional to the rate at which the rabbits and the foxes meet, which, in turn, is proportional to the sizes of their current populations, $x$ and $y$. Therefore, we have: $$\text{rabbits' loss }=\beta\cdot x\cdot y \cdot \Delta t,$$ for some $\beta>0$.
Combined, the change of the rabbit population over the period of time of length $\Delta t$ is: $$\Delta x = \alpha x \Delta t - \beta x y \Delta t.$$
We continue with the foxes. There are two factors affecting their population.
First, we assume that the foxes have only a limited food supply, i.e., the rabbits. The foxes die out geometrically in a manner described previously -- when there is no prey. In other words, the loss of the fox population per unit of time through their natural death is proportional to the size of their current population. Therefore, we have: $$\text{foxes' loss }=\gamma\cdot y \cdot \Delta t,$$ for some $\gamma >0$.
Second, we again assume that the rate of reproduction of the foxes is proportional to the rate of their predation upon the rabbits which is, as we know, proportional to the sizes of their current populations, $x$ and $y$. Therefore, we have: $$\text{foxes' gain }=\delta\cdot x\cdot y \cdot \Delta t,$$ for some $\delta>0$.
Combined, the change of the fox population over the period of time of length $\Delta t$ is: $$\Delta y = \delta xy \Delta t - \gamma y \Delta t.$$
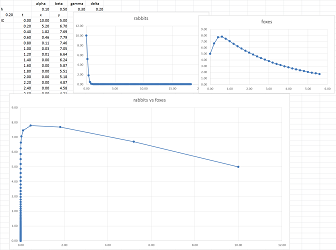
Putting these two together gives us a discrete predator-prey model: $$\begin{cases} \Delta x = \left( \alpha x - \beta x y \right) \Delta t,\\ \Delta y = \left( \delta xy - \gamma y \right) \Delta t. \end{cases}$$ Then the spreadsheet formulas are for $x$ and $y$ respectively: $$\texttt{=R[-1]C+R2C3*R[-1]C*R3C1-R2C4*R[-1]C*R[-1]C[1]*R3C1},$$ $$\texttt{=R[-1]C-R2C5*R[-1]C*R3C1+R2C6*R[-1]C*R[-1]C[-1]*R3C1.}$$
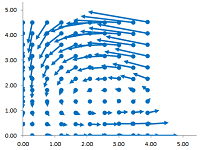
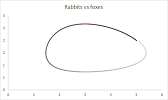
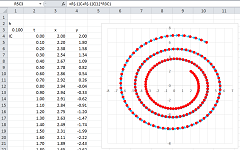
Let's take a look at an example of a possible dynamics ($\alpha=0.10$, $\beta=0.50$, $\gamma=0.20$, $\delta=0.20$, $h=0.2$):
This is what we see. Initially, there are many rabbits and, with this much food, the number of foxes was growing: $\uparrow$. This was causing the number of rabbits to decline: $\leftarrow$. Combined, this is the direction of the system: $\nwarrow$. Later, the number of rabbits declines so much that, with so little food, the number of foxes also started to decline: $\downarrow$. At the end, both of the populations seem to have disappeared...
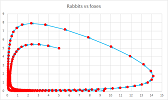
Another experiment shows that they can recover ($\alpha=3$, $\beta=2$, $\gamma=3$, $\delta=1$, $h=0.03$):
In fact, we can see a repeating pattern.
Furthermore, with $\Delta t \to 0$, we have two, related, ODEs, a continuous predator-prey model: $$\begin{cases} \frac{dx}{dt} = \alpha x - \beta x y ,\\ \frac{dy}{dt} = \delta xy - \gamma y . \end{cases}$$ It approximates the discrete model. The equations are known as the Lotka–Volterra equations.
Qualitative analysis of the predator-prey model
To confirm our observations, we will carry out qualitative analysis. It is equally applicable to both the discrete model and the system of ODEs. Indeed, they both have the same right-hand side: $$\begin{cases} \frac{\Delta x}{\Delta t} = \alpha x - \beta x y ,\\ \frac{\Delta y}{\Delta t} = \delta xy - \gamma y , \end{cases}\quad\text{and}\quad \begin{cases} \frac{dx}{dt} = \alpha x - \beta x y ,\\ \frac{dy}{dt} = \delta xy - \gamma y . \end{cases}$$
We will investigate the dynamics at all locations in the first quadrant of the $tx$-plane.
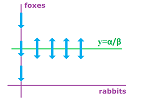
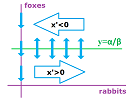
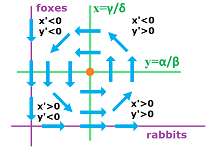
First, we find the locations where $x$ has a zero derivative, i.e., $x'=0$, which is the same as the locations where the discrete model leads to no change in $x$, i.e., $\Delta x=0$. The condition is: $$\alpha x - \beta x y=0.$$ We solve the equation: $$x=0 \text{ or } y=\alpha/\beta.$$ We discover that, first,
- $x=0$ is a solution, and, second,
- the horizontal line $y=\alpha/\beta$ is crossed vertically by the solutions.
In other words, first, the foxes are dying out with no rabbits and, second, there may be a reversal in the dynamics of the rabbits at a certain number of foxes. To find out, solve the inequality: $$x'>0 \text{ or } \Delta x>0\ \Longrightarrow\ \alpha x - \beta x y>0 \ \Longrightarrow\ y<\alpha/\beta.$$ It follows that, indeed, the number of rabbits increases when the number of foxes is below $\alpha/\beta$, otherwise it decreases.
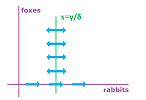
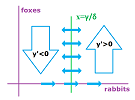
Second, we find the locations where $y$ has a zero derivative, i.e., $y'=0$, which is the same as the locations where the discrete model leads to no change in $y$, i.e., $\Delta y=0$. The condition is: $$\delta xy - \gamma y=0.$$ We solve the equation: $$y=0 \text{ or } x=\gamma/\delta.$$ We discover that, first,
- $y=0$ is a solution, and, second,
- the vertical line $x=\gamma/\delta$ is crossed horizontally by the solutions.
In other words, first, the rabbits thrive with no foxes and, second, there may be a reversal in the dynamics of the foxes at a certain number of rabbits. To find out, solve the inequality: $$y'>0 \text{ or } \Delta y>0\ \Longrightarrow\ \delta xy - \gamma y>0 \ \Longrightarrow\ x>\gamma/\delta.$$ It follows that, indeed, the number of foxes increases when the number of rabbits is above $\gamma/\delta$, otherwise it decreases.
Now we put these two parts together. We have four sectors in the first quadrant determined by the four different choices of the signs of $x'$ and $y'$, or $\Delta x$ and $\Delta y$:
In either case, the result is a rough description of the dynamics on the local level: if this is the current state, then this is the direction it is going. It is a vector field!
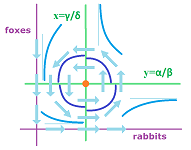
We visualize this vector field with the same parameters as before:
The arrows aren't meant yet to be connected into curves to produce solutions. The only four distinct solutions we know for sure are the following:
- the decline of the foxes in the absence rabbits -- on the $y$-axis;
- the explosion of the rabbits in the absence of foxes -- on the $x$-axis;
- the freezing of both rabbits and foxes at the special levels -- in the middle; and also
- the freezing of both rabbits and foxes at the zero level.
Either of the last two is a constant solution called an equilibrium. The main, non-zero, equilibrium is: $$x(t)=\gamma/\delta,\ y(t)=\alpha/\beta.$$ What about the rest of the solutions?
In order to confirm that the solutions circle the main equilibrium, we need a more precise analysis.
In each of the four sectors, the monotonicity of the solutions has been proven. However, it is still possible that some solutions will stay within the sector when one or both of $x$ and $y$ behave asymptotically: $$x(t)\to a \text{ and/or } y(t)\to b \text{ as } t\to \infty.$$ Since both functions are monotonic, this implies that $$x'(t)\to 0 \text{ and/or } y'(t)\to 0 \text{ as } t\to \infty,$$ and the same for $\Delta x$ and $\Delta y$. We can show that this is impossible. For example, suppose we start in the bottom right sector, i.e., the initial conditions are:
- $x(0)=p>\gamma/\delta$;
- $y(0)=q<\alpha/\beta$.
Then, for as long as the solution is in this sector, we have
- $x'>0 \ \Longrightarrow\ x>p$;
- $y'>0 \ \Longrightarrow\ y>q$.
Therefore, $$y'=y(\delta x - \gamma)>q(\delta p-\gamma)>0.$$ This number is a gap between $y'$ and $0$. Therefore, $y'$ cannot diminish to $0$, and the same is true for $\Delta y$. It follow that the solution will reach the line $y=\alpha/\beta$ “in finite time”.
Exercise. Prove the analogous facts about the three remaining sectors.
We have demonstrated that a solution will go around the main equilibrium, but when it comes back, will it be closer to the center, farther, or will it come to the same location?
The first option is indicated by our spreadsheet result. Next, we set the discrete model aside and concentrate on solving analytically our system of ODEs to answer the question, is this a cycle or a spiral?
Solving the Lotka–Volterra equations
We would like to eliminate time from the equations ($x>0,\ y>0$): $$\begin{cases} \frac{dx}{dt} = \alpha x - \beta x y ,\\ \frac{dy}{dt} = \delta xy - \gamma y . \end{cases}$$ This step is made possible by the following trick. We interpret these derivatives in terms of the differential forms: $$\begin{array}{llll} dx = (\alpha x - \beta x y )dt&\Longrightarrow & dt=\frac{dx}{\alpha x - \beta x y },\\ dy = (\delta xy - \gamma y)dt&\Longrightarrow & dt=\frac{dy}{\delta xy - \gamma y }. \end{array}$$ Therefore, $$dt=\frac{dx}{\alpha x - \beta x y }=\frac{dy}{\delta xy - \gamma y }.$$ We next separate variables: $$\frac{\delta x - \gamma }{x}dx=\frac{\alpha - \beta y}{y}dy.$$ We integrate: $$\int \left(\delta - \frac{\gamma }{x} \right)dx=\int \left(\frac{\alpha}{y} - \beta \right)dy,$$ and we have: $$\delta x - \gamma \ln x = \alpha \ln y - \beta y +C.$$ The system is solved!.. But what does it mean?
Every solution $x=x(t)$ and $y=y(t)$, when substituted into the function $$G(x,y)=\delta x - \gamma \ln x - \alpha \ln y + \beta y,$$ produces a constant. In other words, this parametric curve is a level curve of $z=G(x,y)$.
Exercise. Prove the last statement.
Once we have no derivatives left, we declare the system solved even though only implicitly. Even though we don't have explicit formulas for $x=x(t)$ or $y=y(t)$, we can use what we have to further study the qualitative behavior of the system.
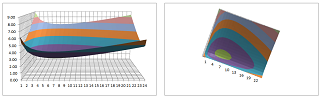
For example, the fact that this is a level curve already suggests that the parametric curve is not a spiral. Just try to imagine such a surface that its level curves are spirals:
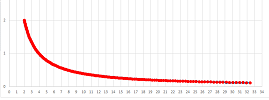
We turn instead to the actual function. First, we plot it with a spreadsheet ($\alpha=3$, $\beta=2$, $\gamma=3$, $\delta=1$):
The level curves are visible. Some of them are clearly circular and others aren't. The reason is that they aren't shown all the way to the axes because the value of $G$ rises so quickly (in fact, asymptotically).
As expected, the surface seems to have a single minimum point. Let's prove that algebraically: $$\begin{array}{lllll} \frac{\partial G}{\partial x}(x,y)&=\delta - \gamma /x,\\ \frac{\partial G}{\partial y}(x,y)&= - \alpha /y + \beta. \end{array}$$ We next find the extreme points of $G$. We set the two derivatives equal to zero and solve for $x$ and $y$: $$\begin{array}{lllll} \frac{\partial G}{\partial x}(x,y)&=\delta - \gamma /x&=0&\Longrightarrow &x=\frac{\gamma}{\delta},\\ \frac{\partial G}{\partial y}(x,y)&= - \alpha /y + \beta&=0&\Longrightarrow &y=\frac{\alpha}{\beta}. \end{array}$$ This point is indeed our main equilibrium point. The surface here has a horizontal tangent plane. We have also demonstrated that there are no others points like that!
But could this be a maximum point? Just as $y=x^3$ crosses the $x$-axis at $0$ degrees, a surface can cross its tangent plane.
We compute the second derivatives: $$\begin{array}{lllll} \frac{\partial^2 G}{\partial x^2}(x,y)&=\gamma \frac{1}{x^2}>0,\\ \frac{\partial^2 G}{\partial y^2}(x,y)&=\alpha \frac{1}{y^2}>0 . \end{array}$$ Both are positive throughout, therefore, either of the cross-sections of the surface along the axes have a minimum point here and it has to stay on one side of the plane. However, it might cross it at other directions. For example, this still might be a saddle point! We invoke the Second Derivative Test from Chapter 9 to resolve this.
We consider the Hessian matrix (discussed in Chapter 18) of $G$. It is the $2\times 2$ matrix of the four partial derivatives of $G$: $$H(x,y) = \begin{pmatrix}\frac{\partial^2 G}{\partial x^2} &\frac{\partial^2 G}{\partial x \partial y}\\ \frac{\partial^2 G}{\partial y \partial x} &\frac{\partial^2 G}{\partial y^2}\end{pmatrix}=\begin{pmatrix} \gamma \frac{1}{x^2} &0\\ 0& \alpha \frac{1}{y^2}\end{pmatrix}.$$ Here, in addition, we have the mixed second derivatives: $$\frac{\partial^2 G}{\partial x \partial y}(x,y)=\frac{\partial^2 G}{\partial y \partial x}(x,y)=0 .$$ Next, we look at the determinant of the Hessian: $$D(x,y)=\det(H(x,y)) = \left( \gamma \frac{1}{x^2}\right)\cdot \left( \alpha \frac{1}{y^2}\right)= \frac{\alpha \gamma}{x^2y^2}>0.$$ It's positive! Therefore, the point is a minimum.
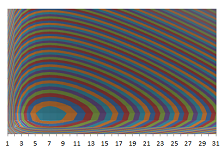
We conclude that every level curve of $G$, i.e., a solution of the system, goes around the equilibrium and comes back to create a cycle.
An easier, but more ad hoc, way to reach this conclusion is to imagine that a solution starts on, say, the line $y=\alpha/\beta$ at $x=x_0$ to the right of the equilibrium and then comes back to the line at $x=x_1$. Since this is a level curve, we have $G(x_0,\alpha/\beta)=G(x_1,\alpha/\beta)$. According to Rolle's Theorem from Chapter 9, this contradicts our conclusion that $\frac{\partial G}{\partial x}> 0$ along this line.
Plotted with the same parameters, this is what these curves look like:
Exercise. Prove that the predator-prey discrete model, i.e., Euler's method for this system of ODEs, produces solutions that spiral away from the equilibrium. Hint: image below.
Vector fields and systems of ODEs
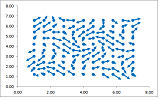
Numerous processes are modeled by systems of ODEs. For example, if little flags are placed on the lawn, then their directions taken together represent a system of ODEs, while the (invisible) air flow is the solutions of this system.
A similar idea is used to model a fluid flow. The dynamics of each particle is governed by the velocity of the flow, at each location, the same at every moment of time.
To solve such a system would require tracing the path of every particle of the liquid.
Let's review the discrete model of a flow: given a flow on a plane, trace a single particle of this stream.
For both coordinates, $x$ and $y$, the following table is being built. The initial time $t_0$ and the initial location $p_0$ are placed in the first row of the spreadsheet. As we progress in time and space, new numbers are placed in the next row of our spreadsheet: $$t_n,\ v_n,\ p_n,\ n=1,2,3,...$$ The following recursive formulas are used:
- $t_{n+1}=t_n+\Delta t$.
- $p_{n+1}=p_n+v_{n+1}\cdot \Delta t$.
The result is a growing table of values: $$\begin{array}{c|c|c|c|c|c} &\text{iteration } n&\text{time }t_n&&\text{velocity }v_n&\text{location }p_n\\ \hline \text{initial:}&0&3.5&&--&22\\ &1&3.6&&33&25.3\\ &...&...&&...&...\\ &1000&103.5&&4&336\\ &...&...&&...&...\\ \end{array}$$
So, instead of two (velocity -- location, as before), there will be four main columns when the motion is two-dimensional and six when it is three-dimensional: $$\begin{array}{c|c|cc|cc|c} \text{}&\text{time}&\text{horiz.}&\text{horiz.}&\text{vert.}&\text{vert.}&...\\ \text{} n&\text{}t&\text{vel. }x'&\text{loc. }x&\text{vel. }y'&\text{loc. }y&...\\ \hline 0&3.5&--&22&--&3&...\\ 1&3.6&33&25.3&4&3.5&...\\ ...&...&...&...&...&...&...\\ 1000&103.5&4&336&66&4&...\\ ...&...&...&...&...&...&...\\ \end{array}$$
Example. Recall the examples such flows. If the velocity of the flow is proportional to the location: $$v_{n+1}=.2\cdot p_n,$$ for both horizontal and vertical, the result is particles flying away from the center, faster and faster:
If the horizontal velocity is proportional to the vertical location and the vertical velocity proportional to the negative of the horizontal location, the result resembles rotation:
$\square$
Now, suppose the velocity comes from explicit formulas as functions of the location: $$u=f(x,y),\ v=g(x,y),$$ are there explicit formulas for the location as a function of time: $$x=x(t),\ y=y(t)?$$
We assume that there is a version of our recursive relation, $$p_{n+1}=p_n+v_{n+1}\cdot \Delta t,$$ for every $\Delta t>0$ small enough. Then our two functions have to satisfy for $x$: $$v_n=f(p_n) \text{ and } p_n=x(t_n),$$ and for $y$: $$v_n=g(p_n) \text{ and } p_n=y(t_n),$$
We substitute these two, as well as $t=t_n$, into the recursive formulas for $p_{n+1}$ for $x$: $$x(t+\Delta t)=x(t)+f(x(t+\Delta t),y(t+\Delta t))\cdot \Delta t,$$ and for $y$: $$y(t+\Delta t)=y(t)+g(x(t+\Delta t),y(t+\Delta t))\cdot \Delta t.$$ Then, we have for $x$: $$\frac{x(t+\Delta t)-x(t)}{\Delta t}=f(x(t+\Delta t),y(t+\Delta t)),$$ and for $y$: $$\frac{y(t+\Delta t)-y(t)}{\Delta t}=g(x(t+\Delta t),y(t+\Delta t)).$$ Taking the limit over $\Delta t\to 0$ gives us the following system: $$\begin{cases} x'(t)&=f(x(t),y(t)),\\ y'(t)&=g(x(t),y(t)), \end{cases}$$ provided $x=x(t),\ y=y(t)$ are differentiable at $t$ and $u=f(x,y),\ v=g(x,y)$ are continuous at $(x(t),y(t))$.
Now, let's recall from Chapter 21 that a vector field supplies a direction to every location, i.e., there is a vector attached to each point of the plane: $${\rm point} \mapsto {\rm vector}.$$ A vector field in dimension $2$ is in fact any function: $$F : {\bf R}^2 \to {\bf R}^2 ,$$ given by two functions of two variables: $$F(x,y)=<f(x,y),g(x,y)>.$$ Then, the vector field defines a system of two (time-independent) ODEs.
Definition. A solution of a system of ODEs is a pair of functions $x=x(t)$ and $y=y(t)$ (a parametric curve) with either one differentiable on an open interval $I$ such that for every $t$ in $I$ we have: $$\begin{cases} x'(t)&=f(x(t),y(t)),\\ y'(t)&=g(x(t),y(t)), \end{cases}$$ or abbreviated: $$\begin{cases} x'=f(x,y),\\ y'=g(x,y). \end{cases}$$
The vector field of this system is the slope field of the ODE.
How do we visualize the solutions of such a system? With a single ODE, $$y'=f(t)\ \Longrightarrow\ y=y(t),$$ we simply plot their graphs, i.e., the collections of points $(t,y(t))$, of some of them on the $ty$-plane. This time, the solutions are parametric curves! Their graphs, i.e., the collections of $(t,x(t),y(t))$ lie in the $3$-dimensional $txy$-space. That is why, we, instead, plot their images, i.e., the collections of points $(x(t),y(t))$ on the $xy$-plane. In the theory of ODEs, they are also known as trajectories, or paths.
Then the vectors of the vector field are tangent to these trajectories.
Since the vector field is independent of $t$, such a representation is often sufficient as explained by the following result.
Theorem. If $x=x(t),\ y=y(t)$ is a solution of the system of ODEs then so is $x=x(t+s),\ y=y(t+s)$ for any real $s$.
It is also important to be aware of the fact that the theory of systems of ODEs “includes” the theory of single ODEs. Recall, first, how the graph of every function can be represented by the trajectory of a parametric curve: $$y=r(x)\ \longrightarrow\ \begin{cases} x=t,\\ y=r(x). \end{cases}$$ Similarly, the solutions of every time-independent ODE can be represented by the trajectories of a system of two ODEs: $$y'=g(x) \ \longrightarrow\ \begin{cases} x'&=1,\\ y'&=g(y). \end{cases}$$
Definition. For a given system of ODEs and a given triple $(t_0,x_0,y_0)$, the initial value problem, or an IVP, is $$\begin{cases} x'&=f(x,y),\\ y'&=g(x,y); \end{cases}\quad \begin{cases} x(t_0)&=x_0,\\ y(t_0)&=y_0; \end{cases}$$ and its solution is a solution of the ODE that satisfies the initial condition above.
By the last theorem, the value of $t_0$ doesn't matter; it can always be chosen to be $0$.
Definition. We say that a system of ODEs satisfies the existence property at a point $(t_0,x_0,y_0)$ when the IVP above has a solution.
If your model of a real-life process doesn't satisfy existence, it reflects limitations of your model. It is as if the process starts but never continues.
Definition. We say that an ODE satisfies the uniqueness property at a point $(t_0,x_0,y_0)$ if every pair of solutions, $(x_1,y_1),\ (x_2,y_2)$, of the IVP above are equal, $$x_1(t)=x_2(t), \ y_1(t)=y_2(t),$$ for every $t$ in some open interval that contains $t_0$.
If your model of a real-life process doesn't satisfy uniqueness, it reflects limitations of your model. It's as if you have all the data but can't predict even the nearest future.
Thus systems of ODEs produce families of curves as the sets of their solutions. Conversely, if a family of curves is given by an equation with a single parameter, we may be able to find a system of ODEs for it.
Example. The family of vertically shifted graphs, $$y=x^2+C,$$ creates an ODE if we differentiate (implicitly) with respect to $t$: $$y'=2xx'.$$ Since these are just functions of $x$, we can choose $x=t$. This is a possible vector field for this family: $$\begin{cases} x'&=1,\\ y'&=2x. \end{cases}$$ $\square$
Example. The family of stretched exponential graphs, $$y=Ce^x,$$ creates an ODEs: $$y'=Ce^xx'.$$ This is a possible vector field for this family: $$\begin{cases} x'&=1,\\ y'&=Ce^x. \end{cases}$$ $\square$
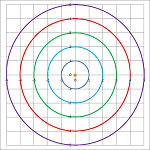
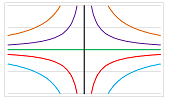
Example. What about these concentric circles?
(In the case when $C=0$, we have the origin.) They are given by $$x^2+y^2=C\ge 0.$$ We differentiate (implicitly) with respect to $t$: $$2xx'+2yy'=0.$$ We choose what $x',\ y'$ might be equal to in order for the two terms to cancel. This is a possible vector field for this family: $$\begin{cases} x'&=-y,\\ y'&=x. \end{cases}$$ $\square$
Example. These hyperbolas are given by these equations: $$xy=C.$$ (In the case when $C=0$, we have the two axes.)
Then, we have an ODE: $$x'y+xy'=0.$$ This is a possible vector field for this family: $$\begin{cases} x'&=x,\\ y'&=-y. \end{cases}$$ $\square$
None of the examples have problems with either existence or uniqueness -- in contrast to the corresponding ODEs.
The proofs of the following important theorems lie outside the scope of this book.
Theorem (Existence). Suppose $(x_0,y_0)$ is a point on the $xy$-plane and suppose
- $H$ is an open interval that contains $x_0$, and
- $G$ is an open interval that contains $y_0$.
Suppose also that functions $z=f(x,y)$ and $z=g(x,y)$ of two variables are continuous with respect to $x$ and $y$ on $H\times G$. Then the system of ODE, $$\begin{cases} x'&=f(x,y),\\ y'&=g(x,y). \end{cases}$$ satisfies the existence property at $(t_0,x_0,y_0)$ for any $t_0$.
Theorem (Uniqueness). Suppose $(x_0,y_0)$ is a point on the $xy$-plane and suppose
- $H$ is an open interval that contains $x_0$, and
- $G$ is an open interval that contains $y_0$.
Suppose also that function $z=f(x,y)$ and $z=g(x,y)$ of two variables are differentiable with respect to $x$ and $y$ on $H\times G$. Then the system of ODEs, $$\begin{cases} x'&=f(x,y),\\ y'&=g(x,y). \end{cases}$$ satisfies the uniqueness property at $(t_0,x_0,y_0)$ for any $t_0$.
Discrete systems of ODEs
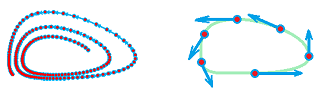
Discrete ODEs approximate and are approximated by continuous ODEs. The same is true for systems. For example, the discrete system for the predator-prey model produces this almost exactly cyclic path:
In other words, Euler's method is capable of tracing solutions very close the ones of the ODE it came from.
Just as in the $1$-dimensional case, the IVP tells us:
- where we are (the initial condition), and
- the direction we are going (the ODE).
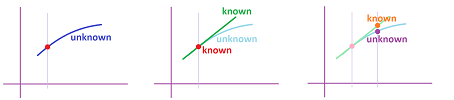
Just as before, the unknown solution is replaced with its best linear approximation.
Example. Let's consider again these concentric circles:
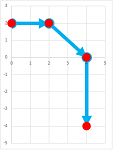
They are the solutions of the ODEs: $$\begin{cases} x'&=y,\\ y'&=-x; \end{cases}$$ We choose the increment of $t$: $$\Delta t=1.$$
We start with this initial condition: $$t_0=0, \quad x_0=0,\quad y_0=2.$$ We substitute these two numbers into the equations: $$\begin{cases} x'&=2,\\ y'&=0; \end{cases}$$ This is the direction we will follow. The increments are $$\begin{cases} \Delta x=2\cdot \Delta t=2\cdot 1 =2,\\ \Delta y=0\cdot \Delta t=0\cdot 1 =0; \end{cases}$$ Our next location on the $xy$-plane is then: $$\begin{cases} x_1=x_0+\Delta x=0+2=2,\\ y_1=y_0+\Delta y=2+0=2. \end{cases}$$
A new initial condition appears: $$x_0=2,\quad y_0=2.$$ We again substitute these two numbers into the equations: $$\begin{cases} x'&=2,\\ y'&=-2; \end{cases}$$ producing the direction we will follow. The increments are $$\begin{cases} \Delta x=2\cdot \Delta t=2\cdot 1 =2,\\ \Delta y=-2\cdot \Delta t=-2\cdot 1 =-2; \end{cases}$$ Our next location on the $xy$-plane is then: $$\begin{cases} x_2=x_1+\Delta x=2+2=4,\\ y_2=y_1+\Delta y=2+(-2)=0. \end{cases}$$
One more IVP: $$x_2=0,\ y_2=-4.$$ The increments are $$\begin{cases} \Delta x=0\cdot \Delta t=0\cdot 1 =0,\\ \Delta y=-4\cdot \Delta t=-4\cdot 1 =-4; \end{cases}$$ Our next location on the $xy$-plane is then: $$\begin{cases} x_3=x_2+\Delta x=4+0=4,\\ y_3=y_2+\Delta y=0-4=-4. \end{cases}$$
These four points form a very crude approximation of one of our circular solutions:
They are clearly spiraling away from the origin. $\square$
In terms of motion,
- at our current location and current time, we examine the ODE to find the velocity and then move accordingly to the next location.
Definition. The Euler solution with increment $\Delta t>0$ of the IVP $$\begin{cases} x'&=f(x,y),\\ y'&=g(x,y); \end{cases}\quad \begin{cases} x(t_0)&=x_0,\\ y(t_0)&=y_0; \end{cases}$$ is the two sequences $\{x_n\}$ and $\{y_n\}$ of real numbers given by: $$\begin{cases} x_{n+1}&=x_n+f(x_n,y_n)\cdot \Delta t,\\ y_{n+1}&=y_n+g(x_n,y_n)\cdot \Delta t; \end{cases}$$ where $t_{n+1}=t_n+\Delta t$.
Once again, if we derived our ODEs from a discrete model (via $\Delta t\to 0$), Euler's method will bring us right back to it: $$\newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccc} &&\text{ODEs}\\ &\nearrow&&\searrow\\ \text{discrete model}&&\la{same!}&&\text{Euler's method} \end{array}$$
Example. Let's now carry out this procedure with a spreadsheet. The formulas for $x_n$ and $y_n$ are respectively: $$\texttt{=R[-1]C+R[-1]C[1]*R3C1},$$ $$\texttt{=R[-1]C-R[-1]C[-1]*R3C1}.$$ These are the results:
In contrast to the case of a single ODE, the approximations do not behave erratically close to the $x$-axis. The reason is that there is no division by $y$ anymore. $\square$
Example. Let's consider again these hyperbolas: $$xy=C.$$ They are the solutions of the system: $$\begin{cases} x'&=x,\\ y'&=-y; \end{cases}$$ An Euler solution is shown below:
However, is this asymptotic convergence toward the $x$-axis or do they merge? $\square$
Qualitative analysis of systems of ODEs
Since Euler's method depends on the value of $h$, the increment of $t$, and, even with smaller and smaller values of $h$, the result remains a mere approximation. Meanwhile, qualitative analysis collects information about the solutions without solving the system -- either analytically or numerically. The result is fully accurate but very broad descriptions of the solutions.
Example. Let's review an example of a single ODE from last section: $$y'=-\tan (y).$$ This is what we conclude about the strip $[-\pi/2,\pi/2]$:
- for $-\pi/2<y<0$, we have $y'=-\tan y>0$ and, therefore, $y\nearrow$;
- for $y=0$, we have $y'=-\tan y=0$ and, therefore, $y$ is a constant solution;
- for $0<y<\pi/2$, we have $y'=-\tan y<0$ and, therefore, $y\searrow$.
In fact, every solution $y$ is decreasing (or increasing) throughout its domain. The conclusions are confirmed with Euler's method:
We can match this ODE with a system: $$\begin{cases} x'=1,\\ y'=-\tan y. \end{cases}$$ Its solutions have these trajectories as solutions. $\square$
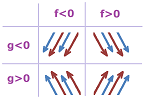
The directions of a parametric curves are its tangent vectors. Therefore, the directions of the solutions of the system of ODEs: $$\begin{cases} x'=f(x,y),\\ y'=g(x,y), \end{cases}$$ are derived from the signs of the functions in the right-hand side: $$\begin{array}{c|c|c|c} &&x'=f(x,y)<0&x'=f(x,y)=0&x'=f(x,y)>0\\ \hline &&\leftarrow&\bullet&\to\\ \hline y'=g(x,y)<0&\downarrow&\swarrow&\downarrow&\searrow\\ \hline y'=g(x,y)=0&\bullet&\leftarrow&\bullet&\rightarrow\\ \hline y'=g(x,y)>0&\uparrow&\nwarrow&\uparrow&\nearrow \end{array}$$
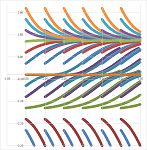
Example. Consider next: $$y'=\cos y \cdot \sqrt{|y|}.$$ we demonstrated that the monotonicity of the solutions varies with the cosine:
We can see that all solutions progress forward along the $x$-axis. What if we add variability of the direction of $x$? Consider: $$\begin{cases} x'=\sin y,\\ y'=\cos y . \end{cases}$$ We conduct the “sign analysis” for both functions in the right-hand side: $$\begin{array}{r|c|c|c} y&x'&x=x(t)&\text{path}\\ \hline 2\pi&0&&\\ &-&x\downarrow&\leftarrow\leftarrow\leftarrow\leftarrow\\ \pi&0&&\\ &+&x\uparrow&\to\to\to\to\\ 0&0&&\\ &-&x\downarrow&\leftarrow\leftarrow\leftarrow\leftarrow\\ -\pi&0&\\ \end{array} \quad \begin{array}{r|c|c|c} y&y'&y=y(t)&\text{path}\\ \hline 3\pi/2&0&\\ &-&y\downarrow&\downarrow\downarrow\downarrow\downarrow\\ \pi/2&0&\\ &+&y\uparrow&\uparrow\uparrow\uparrow\uparrow\\ -\pi/2&0&\\ \end{array}$$ Now put them together: $$\begin{array}{cccccc} \to&\to&\to&\to\\ \nearrow&\nearrow&\nearrow&\nearrow\\ \uparrow&\uparrow&\uparrow&\uparrow\\ \nwarrow&\nwarrow&\nwarrow&\nwarrow\\ \leftarrow&\leftarrow&\leftarrow&\leftarrow\\ \end{array}$$ The results are confirmed with Euler's method:
$\square$
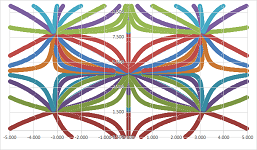
Example. The next one: $$\begin{cases} x'=\sin x,\\ y'=\cos y . \end{cases}$$ We conduct the “sign analysis” of the right-hand side: $$\begin{array}{r|c|cccccc} &x&-\pi&&\pi&&2\pi&&3 \pi&\\ \hline y&y' | x'&0&+&0&-&0&+&0\\ \hline 3\pi/2&0&\bullet&\to&\bullet&\leftarrow&\bullet&\to&\bullet\\ &-&\downarrow&\searrow&\downarrow&\swarrow&\downarrow&\searrow&\downarrow\\ \pi/2&0&\bullet&\to&\bullet&\leftarrow&\bullet&\to&\bullet\\ &+&\uparrow&\nearrow&\uparrow&\nwarrow&\uparrow&\nearrow&\uparrow\\ -\pi/2&0&\bullet&\to&\bullet&\leftarrow&\bullet&\to&\bullet\\ &-&\downarrow&\searrow&\downarrow&\swarrow&\downarrow&\searrow&\downarrow\\ -3\pi/2&0&\bullet&\to&\bullet&\leftarrow&\bullet&\to&\bullet\\ \end{array}$$ The results are confirmed with Euler's method:
$\square$
Example. The next one is discontinuous: $$x'=x−y,\ y'=[x+y].$$ For Euler's method we use the $\texttt{FLOOR}$ function:
$\square$
Exercise. Confirm the plot below by analyzing this system: $$x'=y,\ y'=\sin y \cdot y.$$
Suppose the system is time-independent, $$x'=f(x,y),\ y'=g(x,y).$$ Then it is thought of as a flow: liquid in a pond or the air over a surface of the Earth.
Then, the right-hand side is recognized as a two-dimensional vector field. In contrast to the $1$-dimensional case with only three main possibilities, we will see a wide variety of behaviors around an equilibrium when the space of location is a plane.
With such a system, the qualitative analysis is much simpler. In fact, the ones above exhibit most of the possible patterns of local behavior.
We concentrate on what is going on in the vicinity of a given location $(x,y)=(a,b)$.
The first main possibility is $$f(a,b)\ne 0 \text{ or } g(a,b)\ne 0,$$ which is equivalent to $$F(a,b)= <f(a,b),g(a,b)>\ne 0.$$ Then, from the continuity of $f$ and $g$, we conclude that neither changes its sign in some disk $D$ that contains $(a,b)$. Then, the solutions with paths located within $D$ proceed in an about the same direction:
The behavior is “generic”.
More interesting behaviors are seen around a zero of $F$:
- $F(a,b)=0\ \Longrightarrow\ (x,y)=(a,b) $ is a stationary solution (an equilibrium).
Then the pattern in the vicinity of the point, i.e., an open disk $D$, depends on whether this is a maximum of $f$ or $g$, or a minimum, or neither. Some of the ideas come from dimension $1$.
For example, a stable equilibrium, $$y\to a \text{ as } x\to +\infty,$$ is a sink: flow in only. An unstable equilibrium, $$y\to a \text{ as } x\to -\infty,$$ is a source: flow out only.
An semi-stable equilibrium could mean that some the solutions asymptotically approach the equilibrium and others do not. As you can see there are many more possibilities than in dimension $1$.
The vector notation and linear systems
We can combine the two variables to form a point, a location or a location on the plane: $$X=(x,y).$$ We can also use the column-vector notation: $$X=\left[\begin{array}{cc}x \\ y\end{array}\right].$$ Next, the same happens to their derivatives as vectors: $$\frac{\Delta X}{\Delta t}=\left<\frac{\Delta x}{\Delta t}, \frac{\Delta y}{\Delta t}\right>=\left[\begin{array}{cc}\frac{\Delta x}{\Delta t}\\\frac{\Delta y}{\Delta t}\end{array}\right].$$ Then the setup we have been using for real-valued functions reappears: $$\frac{\Delta X}{\Delta t}=F(X),\ X(t_0)=X_0.$$ In this section, our main concern will be ODEs with respect to derivatives: $$X'=<x',y'>=\left[\begin{array}{cc}x'\\y'\end{array}\right],$$ and $$X'=F(X),\ X(t_0)=X_0.$$ All the plotting, however, is done with the discrete ODEs.
The “phase space” ${\bf R}^2$ is the space of all possible locations. Then the position of a given particle is a function $X:{\bf R}^+\to {\bf R}^2$ of time $t\ge 0$. Meanwhile, the dynamics of the particle is governed by the velocity of the flow, at each location, the same at every moment of time: the velocity of a particle if it happens to be at point $X$ is $F(X)$.
Then either the next position is predicted to be $X+F(X)$ -- that's a discrete model -- or $F(X)$ is just a tangent of the trajectory -- that's an ODE.
A vector field supplies a direction to every location, i.e., there is a vector attached to each point of the plane: $${\rm point} \mapsto {\rm vector}.$$
A vector field in dimension $2$ is any function: $$F : {\bf R}^2 \to {\bf R}^2 .$$ Furthermore, one can think of a vector field as a time-independent ODE on the plane: $$X'=F(X).$$ The corresponding IVP adds an initial condition: $$X(t_0)=X_0.$$
Definition. A solution of a system of ODEs is a function $u$ differentiable on an open interval $I$ such that for every $t$ in $I$ we have: $$X'(t)=F(X(t)).$$
Definition. For a given system of ODEs and a given $(t_0,X_0)$, the initial value problem, or an IVP, is $$X'=F(X),\quad X(t_0)=X_0.$$ and its solution is a solution of the ODE that satisfies the initial condition above.
Definition. The Euler solution with increment $\Delta t>0$ of the IVP: $$X'=F(X),\quad X(t_0)=X_0;$$ is a sequence $\{X_n\}$ of points on the plane given by: $$X_{n+1}=X_n+F(X_n)\cdot \Delta t,$$ where $t_{n+1}=t_n+\Delta t$.
All the definitions above remain valid if we think of $X$ as a location in an $N$-dimensional space ${\bf R}^N$.
We now concentrate on linear systems (that may be acquired from non-linear ones via linearization). All the functions involved are linear and, therefore, differentiable; both existence and uniqueness are satisfied!
This is the case of a linear function $F$. As such, it is given by a matrix and is evaluated via matrix multiplication: $$F(X)=FX=\left[ \begin{array}{ll}a&b\\c&d\end{array}\right] \left[ \begin{array}{ll}x\\y\end{array}\right]=\left[ \begin{array}{ll}ax+by\\cx+dy\end{array}\right].$$ It is written simply as $$X'=FX.$$ The characteristics of this matrix -- the determinant, the trace, and the eigenvalues -- will help us classify such a system.
However, the first observation is very simple: $X=0$ is the equilibrium of the system. In fact what we've learned about systems of linear equations tells us the following.
Theorem. When $\det F\ne 0$, $X=0$ is the only equilibrium of the system $X'=FX$; otherwise, there are infinitely many such points.
In other words, what matter is whether $F$, as a function, is or is not one-to-one.
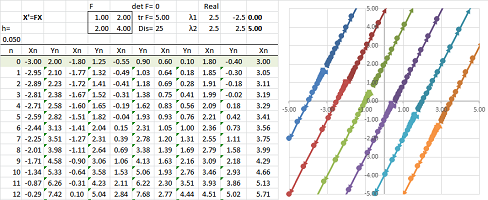
Example (degenerate). The latter is the “degenerate” case such as the following. Let's consider this very simple system of ODEs: $$\begin{cases}x'&=2x\\ y'&=0\end{cases} \qquad\begin{array}{ll}\Longrightarrow\\ \Longrightarrow\end{array} \begin{cases}x&=Ce^{2t}\\ y&=K\end{cases}.$$ It is easy to solve, one equation at a time. We have exponential growth on the $x$-axis and constant on the $y$-axis.
$\square$
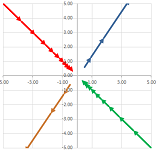
Example (saddle). Let's consider this system of ODEs: $$\begin{cases}x'&=-x\\ y'&=4y\end{cases} \qquad\begin{array}{ll}\Longrightarrow\\ \Longrightarrow\end{array} \begin{cases}x&=Ce^{-t}\\ y&=Ke^{4t}\end{cases}.$$ We solve it instantly because the two variables are fully separated. We can think of either of these two solutions of the two ODEs as a solution of the whole system that lives entirely within one of the two axes:
We have exponential growth on the $x$-axis and exponential decay on the $y$-axis. The rest of the solutions are seen to tend toward one of these. Since not all of the solutions go toward the origin, it is unstable.
This pattern is called a “saddle” because the curves look like the level curves of a function of two variables around a saddle point. Here, the matrix of $F$ is diagonal: $$F=\left[ \begin{array}{ll}-1&0\\0&4\end{array}\right].$$ Algebraically, we have: $$X=\left[ \begin{array}{ll}x\\y\end{array}\right]=\left[ \begin{array}{ll}Ce^{-t}\\Ke^{4t}\end{array}\right]=Ce^{-t}\left[ \begin{array}{ll}1\\0\end{array}\right]+Ke^{4t}\left[ \begin{array}{ll}0\\1\end{array}\right].$$ We have expressed the general solution as a linear combination of the two basis vectors! $\square$
Example (node). A slightly different system is: $$\begin{cases}x'&=2x\\ y'&=4y\end{cases} \qquad\begin{array}{ll}\Longrightarrow\\ \Longrightarrow\end{array} \begin{cases}x&=Ce^{2t}\\ y&=Ke^{4t}\end{cases}.$$ Here, $$F=\left[ \begin{array}{ll}2&0\\0&4\end{array}\right].$$ Once again, either of these two solutions of the two ODEs is a solution of the whole system that lives entirely within one of the two axes (exponential growth on both of the axes) and the rest of the solutions are seen to tend toward one of these. The slight change to the system produces a very different pattern:
Algebraically, we have: $$X=\left[ \begin{array}{ll}x\\y\end{array}\right]=\left[ \begin{array}{ll}Ce^{2t}\\Ke^{4t}\end{array}\right]=Ce^{2t}\left[ \begin{array}{ll}1\\0\end{array}\right]+Ke^{4t}\left[ \begin{array}{ll}0\\1\end{array}\right],$$ a linear combination of the two basis vectors with time-dependent weights. The equilibrium is unstable but changing $2$ and $4$ to $-2$ and $-4$ will reverse the directions of the curves and make it stable. The exponential growth is faster along the $y$-axis; that is why the solutions appear to be tangent to the $x$-axis. In fact, eliminating $t$ gives us $y=x^2$ and similar graphs. When the two coefficients are equal, the growth is identical and the solutions are simply straight lines:
$\square$
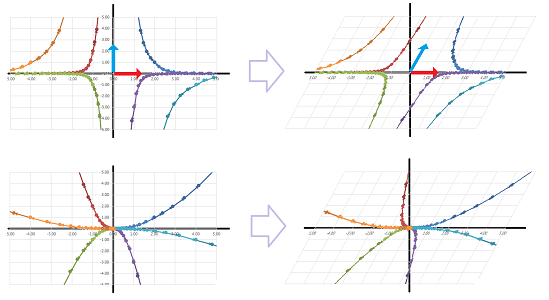
What if the two variables aren't separated? The insight is that they can be -- along the eigenvectors of the matrix. Indeed, the basis vectors are the eigenvectors of these two diagonal matrices. Now just imagine that the two pictures are skewed:
Let's look at them one at a time. The idea is uncomplicated: the system within the eigenspace is $1$-dimensional. In other words, it is a single ODE and can be solved the usual way. This is how we find solutions. Every solution $X$ that lies within the eigenspace, which is a line, is a $t$-dependent multiple of the eigenvector $V$: $$\begin{array}{lll} X=rV& \Longrightarrow X'=(rV)'=F(rV)=rFV=r\lambda V\\ &\Longrightarrow\ r'V=\lambda rV\\ &\Longrightarrow\ r'=\lambda r\\ &\Longrightarrow\ r=e^{\lambda t}. \end{array}$$
Theorem (Eigenspace solutions). If $\lambda$ is an eigenvalue and $V$ a corresponding eigenvector of a matrix $F$, then $$X=e^{\lambda t}V$$ is a solution of the linear system $X'=FX$.
Proof. To verify, we substitute into the equation and use linearity (of both matrix multiplication and differentiation): $$\begin{array}{lll} X=e^{\lambda t}V& \Longrightarrow \\ \text{left-hand side:}&X'=(e^{\lambda t}V)'=(e^{\lambda t})'V=\lambda e^{\lambda t}V;\\ \text{right-hand side:}&FX=F(e^{\lambda t}V)=e^{\lambda t}FV= e^{\lambda t}\lambda V. \end{array}$$ $\square$
The eigenvalue can be complex!
The second idea is to try to express the solution of the general linear system as a linear combination of two solutions found this way.
Theorem (Representation). Suppose $V_1$ and $V_2$ are two eigenvectors of a matrix $F$ that correspond to two eigenvalues $\lambda_1$ and $\lambda_2$. Suppose also that the eigenvectors aren't multiples of each other. Then all solutions of the linear system $X'=FX$ are given as linear combinations of non-trivial solutions within the eigenspaces: $$X=Ce^{\lambda_1 t}V_1+Ke^{\lambda_2 t}V_2,$$ with real coefficients $C$ and $K$.
Proof. Since these solutions cover the whole plane, the conclusion follows from the uniqueness property. $\blacksquare$
Definition. For a given eigenvector $V$ with eigenvalue $\lambda$, we will call $e^{\lambda t}V$ a characteristic solution.
Exercise. Show that when all eigenvectors are multiples of each other, the formula won't give us all the solutions.
Classification of linear systems
We consider a few systems with non-diagonal matrices. The computations of the eigenvalues and eigenvectors come from Chapter 24.
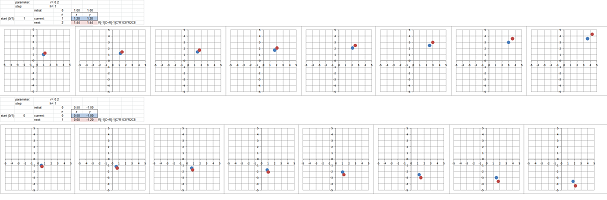
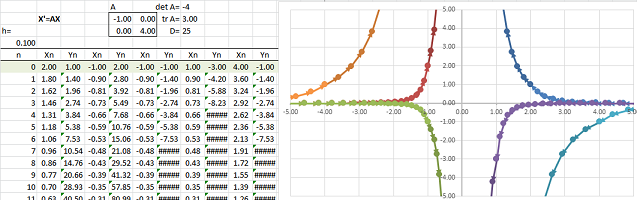
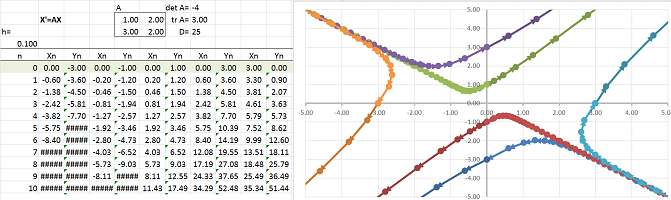
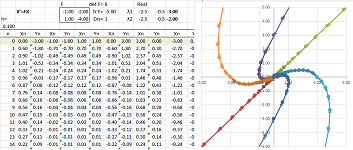
Example (degenerate). Let's consider a more general system of ODEs: $$\begin{cases}x'&=x&+2y,\\ y'&=2x&+4y,\end{cases} \ \Longrightarrow\ F=\left[ \begin{array}{cc}1&2\\2&4\end{array}\right].$$ Euler's method shows the following solutions:
It appears that the system has (exponential) growth in one direction and constant in another. What are those directions? Linear algebra helps.
First, the determinant is zero: $$\det F=\det\left[ \begin{array}{cc}1&2\\2&4\end{array}\right]=1\cdot 4-2\cdot 2=0.$$ That's why there is a whole line of points $X$ with $FX=0$. These are stationary points. To find them, we solve this equation: $$\begin{cases}x&+2y&=0,\\ 2x&+4y&=0,\end{cases} \ \Longrightarrow\ x=-2y.$$ We have, then, eigenvectors corresponding to the zero eigenvalue $\lambda _1=0$: $$V_1=\left[\begin{array}{cc}2\\-1\end{array}\right]\ \Longrightarrow\ FV_1=0 .$$
So, second, there is only one non-zero eigenvalue: $$\det (F-\lambda I)=\det\left[ \begin{array}{cc}1-\lambda&2\\2&4-\lambda\end{array}\right]=\lambda^2-5\lambda=\lambda(\lambda-5).$$ Let's find the eigenvectors for $\lambda_2=5$. We solve the equation: $$FV=\lambda_2 V,$$ as follows: $$FV=\left[ \begin{array}{cc}1&2\\2&4\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=5\left[\begin{array}{cc}x\\y\end{array}\right].$$ This gives as the following system of linear equations: $$\begin{cases}x&+2y&=5x,\\ 2x&+4y&=5y,\end{cases} \ \Longrightarrow\ \begin{cases}-4x&+2y&=0,\\ 2x&-y&=0,\end{cases} \ \Longrightarrow\ y=2x.$$ This line is the eigenspace. We choose the eigenvector to be: $$V_2=\left[\begin{array}{cc}1\\2\end{array}\right].$$
Every solution starts off the line $y=-x/2$ and continues along this vector. It is a linear combination of the two eigenvectors: $$X=CV_1+KV_2=C\left[\begin{array}{cc}2\\-1\end{array}\right]+Ke^{5t}\left[\begin{array}{cc}1\\2\end{array}\right].$$ $\square$
Exercise. Find the line of stationary solutions.
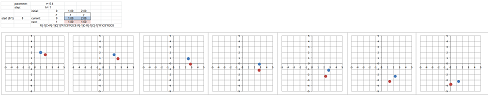
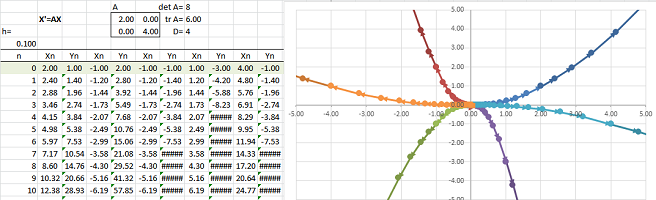
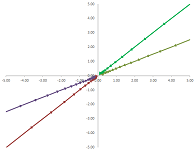
Example (saddle). Let's consider this system of ODEs: $$\begin{cases}x'&=x&+2y,\\ y'&=3x&+2y.\end{cases} $$ Here, the matrix of $F$ is not diagonal: $$F=\left[ \begin{array}{cc}1&2\\3&2\end{array}\right].$$ Euler's method shows the following:
The two lines the solutions appear to converge to are the eigenspaces. Let's find them: $$\det (F-\lambda I)=\det \left[ \begin{array}{cc}1-\lambda&2\\3&2-\lambda\end{array}\right]=\lambda^2-3\lambda-4.$$ Therefore, the eigenvalues are $$\lambda_1=-1,\ \lambda_2=4.$$
Now we find the eigenvectors. We solve the two equations: $$FV_k=\lambda_k V_k,\ k=1,2.$$ The first: $$FV_1=\left[ \begin{array}{cc}1&2\\3&2\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=-1\left[\begin{array}{cc}x\\y\end{array}\right].$$ This gives as the following system of linear equations: $$\begin{cases}x&+2y&=-x,\\ 3x&+2y&=-y,\end{cases} \ \Longrightarrow\ \begin{cases}2x&+2y&=0,\\ 3x&+3y&=0,\end{cases} \ \Longrightarrow\ x=-y.$$ We choose $$V_1=\left[\begin{array}{cc}1\\-1\end{array}\right].$$ Every solution within this eigenspace (the line $y=-x$) is a multiple of this characteristic solution: $$X_1=e^{\lambda_1t}V_1=e^{-t}\left[\begin{array}{cc}1\\-1\end{array}\right].$$
The second eigenvalue: $$FV_2=\left[ \begin{array}{cc}1&2\\3&2\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=4\left[\begin{array}{cc}x\\y\end{array}\right].$$ We have the following system: $$\begin{cases}x&+2y&=4x,\\ 3x&+2y&=4y,\end{cases} \ \Longrightarrow\ \begin{cases}-3x&+2y&=0,\\ 3x&-2y&=0,\end{cases}\ \Longrightarrow\ x=2y/3.$$ We choose $$V_2=\left[\begin{array}{cc}1\\3/2\end{array}\right].$$ Every solution within this eigenspace (the line $y=3x/2$) is a multiple of this characteristic solution: $$X_2=e^{\lambda_2t}V_2=e^{4t}\left[\begin{array}{cc}1\\3/2\end{array}\right].$$
The two solutions $X_1$ and $X_2$, as well as $-X_1$ and $-X_2$, are shown below:
The general solution is a linear combination of these two basic solutions: $$X=Ce^{\lambda_1t}V_1+Ke^{\lambda_2t}V_2=Ce^{-t}\left[\begin{array}{cc}1\\-1\end{array}\right]+Ke^{4t}\left[\begin{array}{cc}1\\3/2\end{array}\right]=\left[\begin{array}{cc}Ce^{-t}+Ke^{4t}\\-Ce^{-t}+3/2Ke^{4t}\end{array}\right],$$ i.e., $$\begin{cases}x&=Ce^{-t}&+Ke^{4t},\\ y&=-Ce^{-t}&+3/2Ke^{4t}.\end{cases} $$ The equilibrium is unstable. $\square$
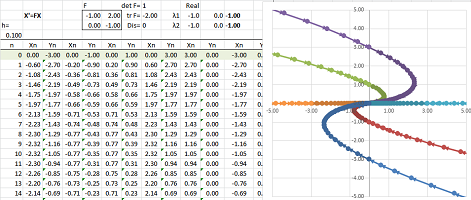
Example (node). Let's consider this system of ODEs: $$\begin{cases}x'&=-x&-2y,\\ y'&=x&-4y.\end{cases} $$ Here, the matrix of $F$ is not diagonal: $$F=\left[ \begin{array}{cc}-1&-2\\1&-4\end{array}\right].$$ Euler's method shows the following:
The analysis starts with the characteristic polynomial: $$\det (F-\lambda I)=\det \left[ \begin{array}{cc}-1-\lambda&-2\\1&-4-\lambda\end{array}\right]=\lambda^2-5\lambda+6.$$ Therefore, the eigenvalues are $$\lambda_1=-3,\ \lambda_2=-2.$$
To find the eigenvectors, we solve the two equations: $$FV_k=\lambda_k V_k,\ k=1,2.$$ The first: $$FV_1=\left[ \begin{array}{cc}-1&-2\\1&-4\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=-1\left[\begin{array}{cc}x\\y\end{array}\right].$$ This gives as the following system of linear equations: $$\begin{cases}-x&-2y&=-3x,\\ x&-4y&=-3y,\end{cases} \ \Longrightarrow\ \begin{cases}2x&-2y&=0,\\ x&-y&=0,\end{cases} \ \Longrightarrow\ x=y.$$ We choose $$V_1=\left[\begin{array}{cc}1\\1\end{array}\right].$$ Every solution within this eigenspace (the line $y=x$) is a multiple of this characteristic solution: $$X_1=e^{\lambda_1t}V_1=e^{-3t}\left[\begin{array}{cc}1\\1\end{array}\right].$$
The second eigenvalue: $$FV_2=\left[ \begin{array}{cc}-1&-2\\1&-4\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=-2\left[\begin{array}{cc}x\\y\end{array}\right].$$ We have the following system: $$\begin{cases}-x&-2y&=-2x,\\ x&-4y&=-2y,\end{cases} \ \Longrightarrow\ \begin{cases}x&-2y&=0,\\ x&-2y&=0,\end{cases}\ \Longrightarrow\ x=2y.$$ We choose $$V_2=\left[\begin{array}{cc}2\\1\end{array}\right].$$ Every solution within this eigenspace (the line $y=x/2$) is a multiple of this this characteristic solution: $$X_2=e^{\lambda_2t}V_2=e^{-2t}\left[\begin{array}{cc}2\\1\end{array}\right].$$
The two solutions $X_1$ and $X_2$, as well as $-X_1$ and $-X_2$, are shown below:
The general solution is a linear combination of these two basic solutions: $$X=Ce^{\lambda_1t}V_1+Ke^{\lambda_2t}V_2=Ce^{-3t}\left[\begin{array}{cc}1\\1\end{array}\right]+Ke^{-2t}\left[\begin{array}{cc}2\\1\end{array}\right].$$ The equilibrium is stable. $\square$
Definition. For a linear system $X'=FX$, the equilibrium solution $X_0=0$ is called a stable node if every other solution $X$ satisfies: $$X(t)\to 0\text{ as } t\to +\infty \text{ and }||X(t)||\to \infty \text{ as } t\to -\infty ;$$ and an unstable node if $$X(t)\to 0\text{ as } t\to -\infty \text{ and }||X(t)||\to \infty \text{ as } t\to +\infty ;$$ provided no $X$ makes a full rotation around $0$.
Definition. For a linear system $X'=FX$, the equilibrium solution $X_0=0$ is called a saddle if it has solutions $X$ that satisfy: $$||X(t)||\to \infty \text{ as } t\to \pm\infty .$$
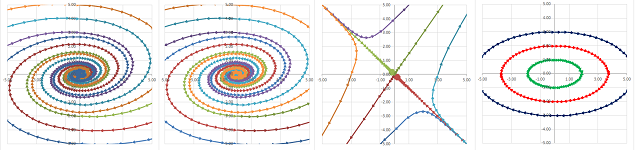
Theorem (Classification of linear systems I). Suppose matrix $F$ has two real eigenvalues $\lambda _1$ and $\lambda_2$. Then,
- if $\lambda _1$ and $\lambda_2$ have the same sign, the system $X'=FX$ has a node, stable when this sign is negative and unstable when this sign is positive;
- if $\lambda _1$ and $\lambda_2$ have the opposite signs, the system $X'=FX$ has a saddle.
Proof. The stability is seen in either of the two characteristic solutions, as $t\to +\infty$: $$||X||=||e^{\lambda t}V||=e^{\lambda t}\cdot ||V||\to\begin{cases}\infty&\text{if }\lambda>0,\\0&\text{if }\lambda<0.\end{cases}$$ According to the last theorem, we have a linear combination of the two characteristic solutions. Then, in the former case, we have one or the other pattern, and in the latter, both. There can be no rotation because no solution can intersect an eigenspace, according to the uniqueness property. $\blacksquare$
Classification of linear systems, continued
What if the eigenvalues are complex?
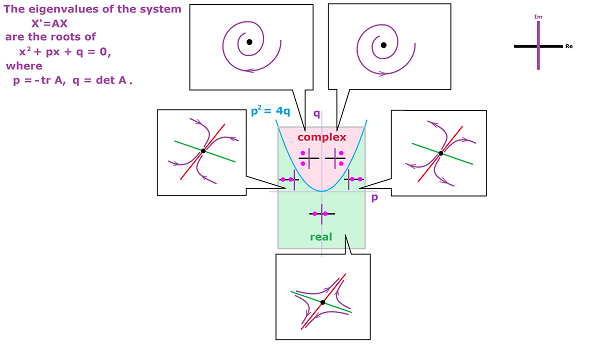
Recall that the characteristic polynomial of matrix $F$ is $$\chi(\lambda)=\det (F-\lambda I)=\lambda^2-\operatorname{tr} F\cdot\lambda+\det F$$ The discriminant of this quadratic polynomial is $$D=(\operatorname{tr} F)^2-4\det F.$$ When $D>0$, we have two distinct real eigenvalues, the case addressed in the last section. We are faced with complex eigenvalues whenever $D<0$. The transitional case is $D=0$.
Example (improper node). In contrast to the last example, a node may be produced by a matrix with repeated (and, therefore, real) eigenvalues: $$F=\left[ \begin{array}{cc}-1&2\\0&-1\end{array}\right].$$ Euler's method shows the following:
The analysis starts with the characteristic polynomial: $$\det (F-\lambda I)=\det \left[ \begin{array}{cc}-1-\lambda&2\\0&-1-\lambda\end{array}\right]=(-1-\lambda)^2.$$ Therefore, the eigenvalues are $$\lambda_1=\lambda_2=-1.$$ The only eigenvectors are horizontal. The solution is given by $$X=Ce^{-t}\left[\begin{array}{cc}1\\0\end{array}\right]+K\left( te^{-t}\left[\begin{array}{cc}1\\0\end{array}\right]+e^{-t}\left[\begin{array}{cc}?\\1\end{array}\right] \right).$$ $\square$
Exercise. Finish the computation in the example.
When $D<0$, the eigenvalues are complex! Therefore, there are no eigenvectors (not real ones anyway). Does the system $X'=FX$ even have solutions? The theorem about characteristic solutions says yes, they are certain exponential functions...
Example (center). Consider $$\begin{cases}x'&=y,\\ y'&=-x.\end{cases} $$ We already know that the solution is found by substitution: $$x' '=(x')'=y'=-x.$$ Therefore the solutions are the linear combinations of $\sin t$ and $\cos t$. The result is confirmed with Euler's method (with a limited number of step to prevent the approximations to spiral out):
According to the theory above, the solutions are supposed to be exponential rather than trigonometric. But the latter are just exponential functions with imaginary exponents.
Let's make this specific; we have $$F=\left[ \begin{array}{ccc}0&1\\-1&0\end{array}\right],$$ and the characteristic polynomial, $$\chi(\lambda)=\lambda^2+1,$$ has these complex roots: $\lambda_{1,2}=\pm i$.
To find the first eigenvector, we solve: $$FV_1=\left[ \begin{array}{ccc}0&1\\-1&0\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=i\left[\begin{array}{cc}x\\y\end{array}\right].$$ This gives as the following system of linear equations: $$\begin{cases}&y&=ix\\ -x&&=iy\end{cases} \ \Longrightarrow\ y=ix.$$ We choose a complex eigenvector: $$V_1=\left[\begin{array}{cc}1\\i\end{array}\right],$$ and similarly: $$V_2=\left[\begin{array}{cc}1\\-i\end{array}\right],$$
The general solution is a linear combination -- over the complex numbers -- of these two characteristic solutions: $$X=Ce^{\lambda_1t}V_1+Ke^{\lambda_2t}V_2=Ce^{it}\left[\begin{array}{cc}1\\i\end{array}\right]+Ke^{-it}\left[\begin{array}{cc}1\\-i\end{array}\right].$$ The problem is solved! ...in the complex domain. What is the real part?
Let $K=0$. Then the solution is: $$X=Ce^{it}\left[\begin{array}{cc}1\\i\end{array}\right]=C\left[\begin{array}{cc}e^{it}\\ie^{it}\end{array}\right]=C\left[\begin{array}{cc}\cos t+i\sin t\\i(\cos t+i\sin t)\end{array}\right]=C\left[\begin{array}{cc}\cos t+i\sin t\\ -\sin t+i\cos t\end{array}\right].$$ Its real part is: $$\operatorname{Re} X=C\left[\begin{array}{cc}\cos t\\ -\sin t\end{array}\right].$$ These are all the circles. $\square$
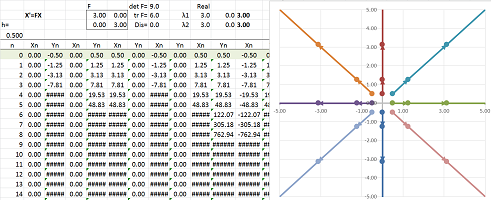
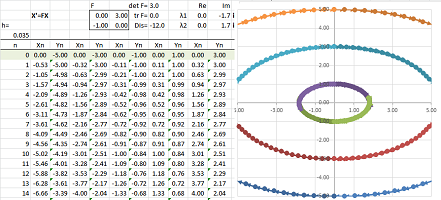
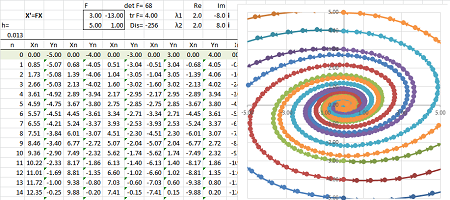
Example (focus). Let's consider a more complex system ODEs: $$\begin{cases}x'&=3x&-13y,\\ y'&=5x&+y.\end{cases} $$ Here, the matrix of $F$ is not diagonal: $$F=\left[ \begin{array}{cc}3&-13\\5&1\end{array}\right].$$ Euler's method shows the following:
The analysis starts with the characteristic polynomial: $$\chi(\lambda)=\det (F-\lambda I)=\det \left[ \begin{array}{cc}3-\lambda&-13\\5&1-\lambda\end{array}\right]=\lambda^2-4\lambda+68.$$ Therefore, the eigenvalues are $$\lambda_{1,2}=2\pm 8i.$$
Now we find the eigenvectors. We solve the two equations: $$FV_k=\lambda_k V_k,\ k=1,2.$$ The first: $$FV_1=\left[ \begin{array}{cc}3&-13\\5&1\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=(2+8i)\left[\begin{array}{cc}x\\y\end{array}\right].$$ This gives as the following system of linear equations: $$\begin{cases}3x&-13y&=(2+8i)x\\ 5x&+y&=(2+8i)y\end{cases} \ \Longrightarrow\ \begin{cases}(1-8i)x&-13y&=0\\ 5x&+(-1-8i)y&=0\end{cases} \ \Longrightarrow\ x=\frac{1+8i}{5}y.$$ We choose $$V_1=\left[\begin{array}{cc}1+8i\\5\end{array}\right].$$
The second eigenvalue: $$FV_2=\left[ \begin{array}{cc}3&-13\\5&1\end{array}\right]\left[\begin{array}{cc}x\\y\end{array}\right]=(2- 8i)\left[\begin{array}{cc}x\\y\end{array}\right].$$ We have the following system: $$\begin{cases}3x&-13y&=(2-8i)x\\ 5x&+y&=(2-8i)y\end{cases} \ \Longrightarrow\ \begin{cases}(1+8i)x&-13y&=0\\ 5x&+(-1+8i)y&=0\end{cases}\ \Longrightarrow\ x=\frac{1-8i}{5}y.$$ We choose $$V_2=\left[\begin{array}{cc}1-8i\\5\end{array}\right].$$
The general complex solution is a linear combination of the two characteristic solutions: $$Z=Ce^{\lambda_1t}V_1+Ke^{\lambda_2t}V_2=Ce^{(2+8i)t}\left[\begin{array}{cc}1+8i\\5\end{array}\right]+Ke^{(2-8i)t}\left[\begin{array}{cc}1-8i\\5\end{array}\right].$$
Let's now examine a simple real solution. We let $C=1$ and $K=0$: $$\begin{array}{lll} X=\operatorname{Re} Z&= \operatorname{Re}e^{(2+8i)t}\left[\begin{array}{cc}1+8i\\5\end{array}\right]\\ &=e^{2t}\operatorname{Re}e^{8it}\left[\begin{array}{cc}1+8i\\5\end{array}\right]\\ &=e^{2t}\operatorname{Re}(\cos 8t+i\sin 8t)\left[\begin{array}{cc}1+8i\\5\end{array}\right]\\ &=e^{2t}\operatorname{Re}\left[\begin{array}{cc}(\cos 8t+i\sin 8t)(1+8i)\\(\cos 8t+i\sin 8t)5\end{array}\right]\\ &=e^{2t}\operatorname{Re}\left[\begin{array}{cc}\cos 8t+i\sin 8t+8i\cos 8t-8\sin 8t\\5\cos 8t+i5\sin 8t\end{array}\right]\\ &=e^{2t}\left[\begin{array}{cc}\cos 8t-8\sin 8t\\5\cos 8t\end{array}\right]. \end{array}$$ Plotting this parametric curve confirms Euler's method result:
$\square$
Definition. For a linear system $X'=FX$, the equilibrium solution $X_0=0$ is called a stable focus if every other solution $X$ satisfies: $$X(t)\to 0\text{ as } t\to +\infty \text{ and }||X(t)||\to \infty \text{ as } t\to -\infty ;$$ and an unstable focus if $$X(t)\to 0\text{ as } t\to -\infty \text{ and }||X(t)||\to \infty \text{ as } t\to +\infty ;$$ provided every such $X$ makes a full rotation around $0$.
Definition. For a linear system $X'=FX$, the equilibrium solution $X_0=0$ is called a center if all solutions are cycles.
Theorem (Classification of linear systems II). Suppose matrix $F$ has two complex conjugate eigenvalues $\lambda _1$ and $\lambda_2$. Then,
- if the real part of $\lambda _1$ and $\lambda_2$ is non-zero, the system $X'=FX$ has a focus, stable when this sign of this number is negative and unstable when this sign is positive;
- if the real part of $\lambda _1$ and $\lambda_2$ is zero, the system $X'=FX$ has a center.
Proof. The stability is seen in either of the two characteristic solutions, as $t\to +\infty$: $$||X||=||e^{\lambda t}V||=||e^{(a+bi) t}V||=e^{at} |\cos bt+i\sin bt|\cdot ||V||=e^{at}||V||\to\begin{cases}\infty&\text{if }a>0,\\0&\text{if }a<0.\end{cases}$$ $\blacksquare$
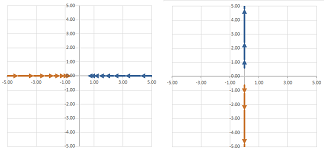
The combination of the two classification theorems is illustrated below:
Thereby we complete the sequence: elementary algebra $\longrightarrow$ matrix algebra $\longrightarrow$ linear differential equations. To summarize, in order to classify a system of linear ODEs $X'=FX$, where $F$ is a $2\times 2$ matrix and $X$ is a vector on the plane, we classify $F$ according to its eigenvalues and visualize how the locations of these two numbers in the complex plane indicate very different behaviors of the trajectories. (The missing patterns are better illustrated dynamically, as the exact “moments” when one pattern transitions into another.)
Exercise. Point out on the complex plane the locations of the center and the improper node.
Exercise. How likely would a given system fall into each of these five categories? What about the center and the improper node?
Exercise. What parameters determine the clockwise vs. counter-clockwise behavior?
Example (predator-prey). Let's classify the equilibria of the predator-prey model -- via linearization. Our non-linear system is given by the following: $$\begin{cases} x' = \alpha x &- \beta x y ,\\ y' = \delta xy &- \gamma y , \end{cases}$$ with non-negative coefficients $\alpha x,\ \beta,\ \delta,\ \gamma$. In other words, we have $$X'=G(X),\text{ with } G(x,y)=(\alpha x - \beta x y ,\delta xy - \gamma y).$$ The Jacobian of $G$ is $$G'(x,y)= \left[\begin{array}{cc} \frac{\partial}{\partial x}(\alpha x - \beta x y)&\frac{\partial}{\partial y}(\alpha x - \beta x y)\\ \frac{\partial}{\partial x}(\delta xy - \gamma y)&\frac{\partial}{\partial y}(\delta xy - \gamma y) \end{array}\right]=\left[\begin{array}{cc} \alpha - \beta y&-\beta x \\ \delta y &\delta x - \gamma \end{array}\right].$$ The matrix depends on $(x,y)$ because the system is non-linear. By fixing locations $X=A$, we create linear vector ODEs: $$X'=G'(A)X.$$
First, we consider the zero equilibrium, $$x=0,\ y=0.$$ Here, $$F=G'(0,0)=\left[\begin{array}{cc} \alpha - \beta \cdot0&-\beta \cdot0 \\ \delta \cdot0 &\delta\cdot 0 - \gamma \end{array} \right] =\left[\begin{array}{cc} \alpha &0 \\ 0& - \gamma \end{array} \right].$$ The eigenvalues are found by solving the following equation: $$\det \left[\begin{array}{cc} \alpha-\lambda &0 \\ 0& - \gamma-\lambda \end{array} \right]=(\alpha-\lambda)(- \gamma-\lambda)=0.$$ Therefore, $$\lambda_1=\alpha,\ \lambda_2=-\gamma.$$ We have two real eigenvalues of opposite signs. This is a saddle! Indeed, around this point the foxes decline while the rabbits increase in numbers.
The main equilibrium is $$x=\frac{\gamma}{\delta},\ y=\frac{\alpha}{\beta}.$$ Here, $$F=G'\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right)=\left[\begin{array}{cc} \alpha - \beta \cdot \frac{\alpha}{\beta} &-\beta \cdot \frac{\gamma}{\delta} \\ \delta \cdot \frac{\alpha}{\beta} &\delta\cdot \frac{\gamma}{\delta} - \gamma \end{array}\right] =\left[\begin{array}{cc} 0 &- \frac{\beta\gamma}{\delta} \\ \frac{\delta\alpha}{\beta} &0 \end{array}\right] .$$ The eigenvalues are found by solving the following equation: $$\det \left[\begin{array}{cc} -\lambda &- \frac{\beta\gamma}{\delta} \\ \frac{\delta\alpha}{\beta} &-\lambda \end{array}\right]=\lambda^2+ \alpha\gamma=0.$$ Therefore, $$\lambda_1=\sqrt{\alpha\gamma}\,i,\ \lambda_2=-\sqrt{\alpha\gamma}\,i.$$ We have two purely imaginary eigenvalues. This is a center! Indeed, around this point we have a cyclic behavior.
The results match our previous analysis. $\square$